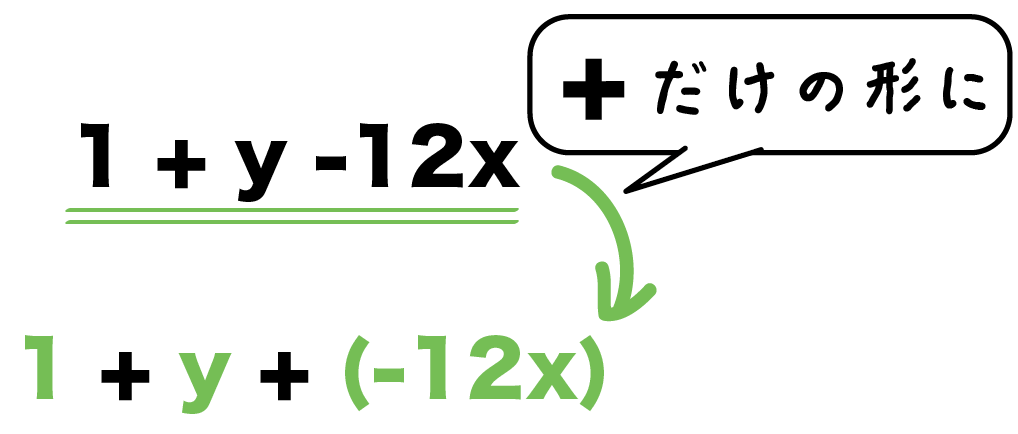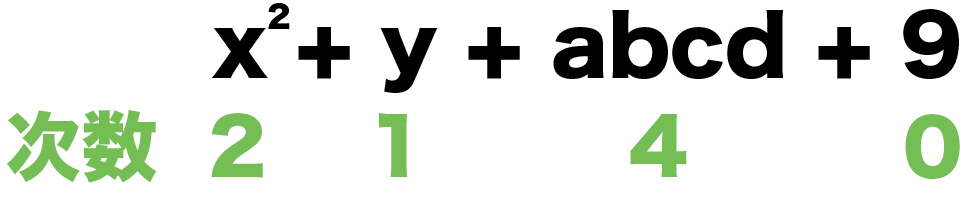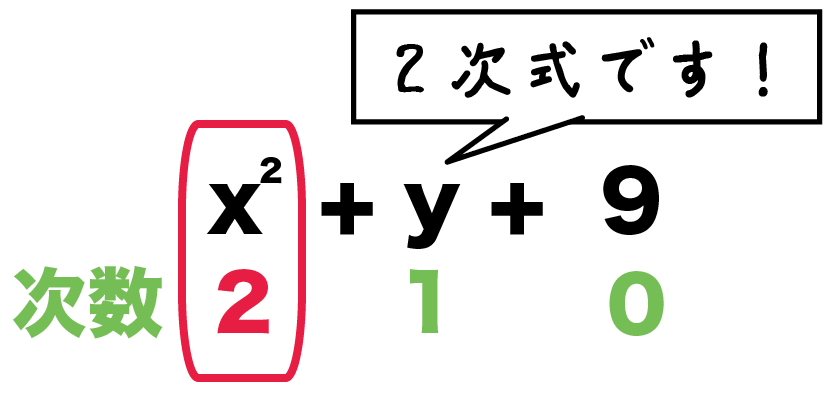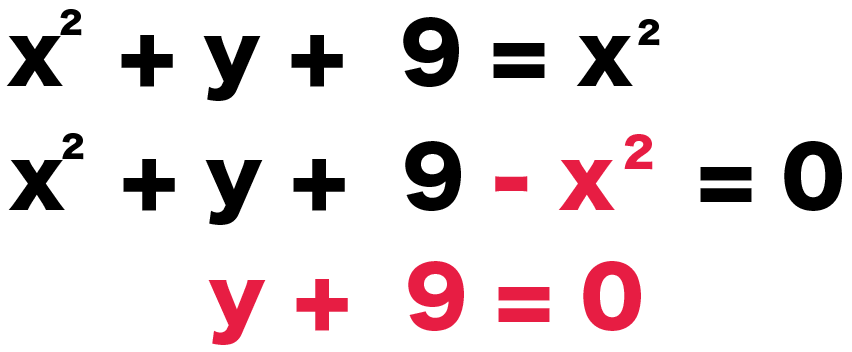3分でわかる!二次方程式とはなんだろう??
二次方程式とはいったいなにもの!?
こんにちは!この記事をかいているKenだよ。業者よびたいね。
中3数学の大きなとりで。
それは、
二次方程式
っていう単元だ。
因数分解や平方根をガンガンつかうから、中3数学の総まとめってかんじ。
けっこう、手強いよ。
今日は、この単元の基礎をおさえるために、
2次方程式とはいったいなにものか??
を勉強していこう。
二次方程式とはずばり・・・!?
さっそくいっちゃうね。
二次方程式とは、
二次式をふくむ方程式のこと
だ。
すごくシンプルだね。
えっ。二次式とか方程式とかわからないって??
そういうときは、つぎの順番に復習すればしっくりくるよ。
- 項とは?
- 次数とは?
- 2次式とは?
- 方程式とは?
中1の復習! 項とはなんだっけ!?
「項」の意味をふりかえってみよう。
項の意味がはっきりすると、次数の意味がわかるからね。
項とはずばり、
+ で結ばれた1つ1つの塊のことだよ。
たとえば、
1 + y -12x
っていう式があったとしよう。
「+」でつながってる形になおすと、
1 + y + (-12x)
になるね。
項は「+でつながってる塊」だったよね??
だから、この式にふくまれる項は、
- 1
- y
- -12x
の3つだ。
項の意味もおっけー!
次数とはなんだっけ!?
次数とはずばり、
1つの項にかけられてる文字の数
だ。
たとえば、さっきの「-12x」に注目してみて。
こいつの次数は「1」だよ。
なぜなら、項にかけられてる文字の数が「1」だからね。
xしか、かかってないもん。
もし、xが2乗だったら次数は「2」になるし、
xとyとzがかかってたら次数は「3」になるわけ。
どう??次数もマスターしたかな??
二次式とはなんだろう??
二次式とはずばり、
いちばん大きな次数が2の式
のことだ。
ちょっと複雑だね。
たとえば、
x² + y + abcd + 9
をイメージして。
項の次数を確認すると、
- xの2乗:次数2
- y:次数1
- abcd:次数4
- 9 : 次数0
になってるね。
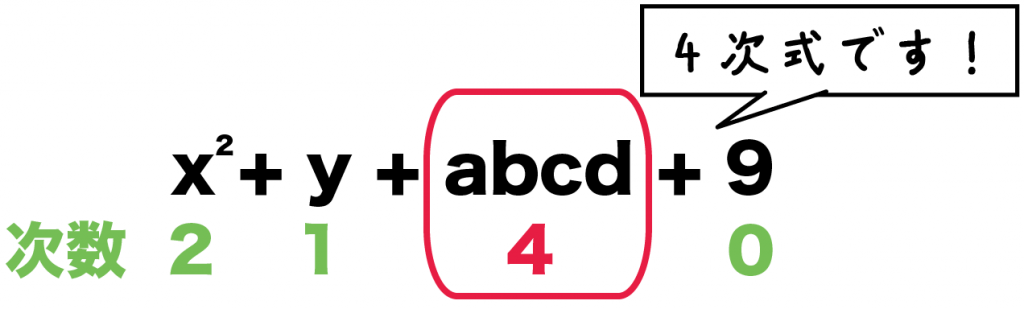
いちばん大きい次数は「abcd」の4だね??
ってことは、
この多項式は「4次式」になるんだ。
もし、「abcd」が消えたとしたら、この式は二次式になる。
x² + y + 9
なぜなら、いちばん大きい次数が「xの2乗」の2だからね。
方程式とはなんだろう??
「方程式」を復習してみよう。
方程式とはずばり、
未知の文字をふくむ等式のこと
だね。
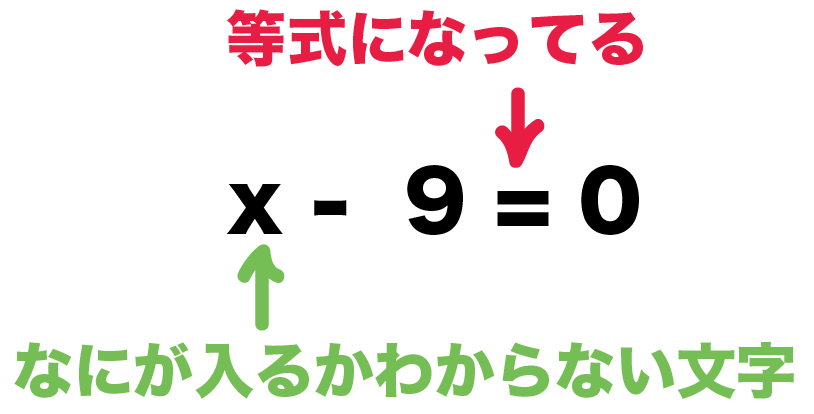
たとえば、
x – 9 =0
とかとかだね。
何がはいるかわからない「文字」があって、
左右が「=」で結ばれてる式
は方程式なんだ。
だから、二次方程式とは、
未知の文字がある等式で、なおかつ、
二次式になってるもの
だね。
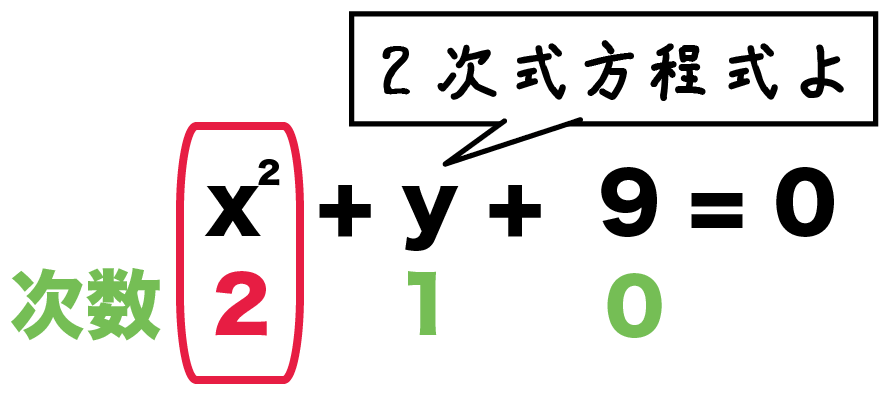
たとえば、さっきの二次式の「x² + y +9 」に「=0」をつけると、
x² + y +9 = 0
になる。
こいつはガチガチの2次方程式だ。
だって、二次式だし、等式だし、未知の文字がふくまれてるからね。
エセ2次方程式に気をつけろ!!
最後に1つだけ注意点があるよ。
それは、
移項とか同類項をまとめ終わって次数を調べる
ってこと。
整理しないまま方程式の次数を数えるのは危険なんだ。
たとえば、
x² + y +9 = x²
っていう方程式をイメージしてみて。
次数をかぞえてみると、
- xの2乗:次数2
- y:次数1
- 9:次数0
- xの2乗:次数2
になってるよね??
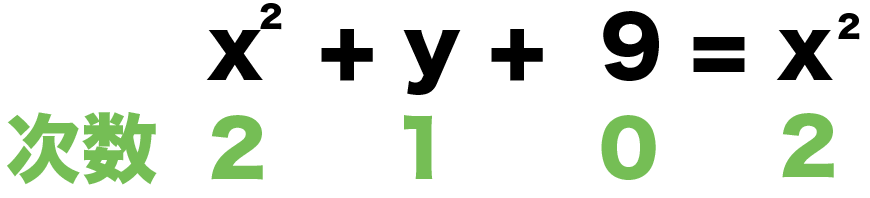
いちばん大きな次数は「2」。
二次方程式じゃないかって思うよね??
だけどね、こいつは二次方程式じゃない。
右辺の「x²」を左辺に移項して、同類項をまとめると、
x² + y +9 = x²
x² + y +9 – x² = 0
y +9 = 0
になるね!
この「y + 9 = 0」っていう方程式で改めて次数をみてみると、
- y : 次数1
- 9 : 次数0
になってる。
最高の次数は1だから、こいつは一次式ってわけなのさ。
ってことで、
移項や同類項が終わって次数を数えてみよう!
まとめ:二次方程式は最高の次数が2の方程式のこと!
二次方程式の正体もわかったかな??
簡単にいうと、
二次式をふくむ方程式。
もっとわかりやすくいうと、
移項とか終わったら、各項の次数を数えてみて、
最高の次数が「2」の方程式のこと
になるんだ。
迷ったときは基本に戻ってみよう。
そんじゃねー
Ken