【三平方の定理】直角三角形の辺の長さを計算する4つの問題の解き方
三平方の定理を使って直角三角形の辺の長さを計算したい!
どうも、Drリードだぞい。
中3数学では、
三平方の定理(ピタゴラスの定理)を勉強してきたよな?
簡単に復習すると、
直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、
a²+ b² = c² が成り立つ
ってやつだったな。

さあ、この定理を使いこなせるようになるんだぞ。
今回はそのための基礎トレーニングだ。
三平方の定理を使って直角三角形の辺の長さを求める4つの問題
三平方の定理をつかった問題でよく出てくるのは、
直角三角形の辺の長さを求める問題。
今日はこの問題を4つのパターンに分けてみたぞ。
- 超基本タイプ
- 平方根の計算混じるタイプ
- 直角二等辺三角形
- 三角形が2つ合体タイプ
問題集では、いろいろな直角三角形がでてくるし、簡単なのも難しいのも混じっているからな。
初めは解けなくっても、がっくりこないで、
負けんぞ!!
と構えとけ。

問題1. 「公式で求める基本タイプ」
まず1つ目の問題は、
直角三角形の辺の長さを三平方の定理の公式で求めるタイプ。
これは、
三平方の定理の公式に、辺の長さを代入して計算するだけだから簡単だ。
たとえば、つぎの練習問題な。
練習問題1.
つぎの直角三角形の辺の長さxを求めてください。
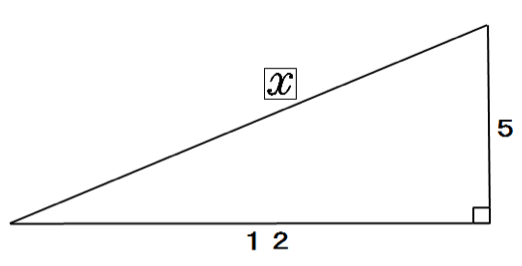
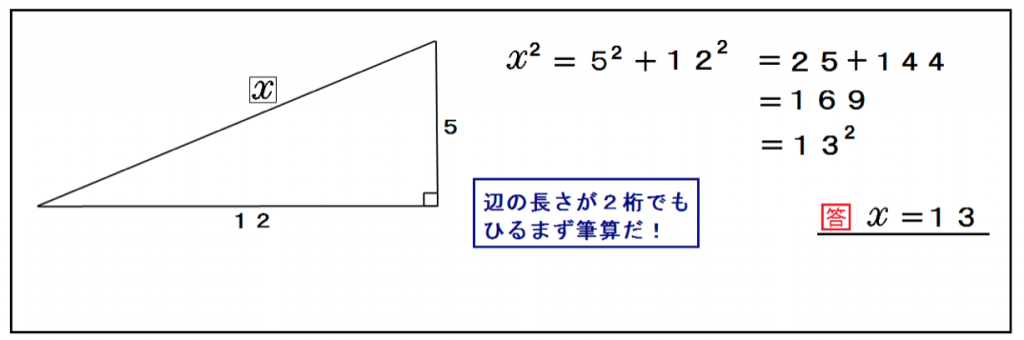
辺の長さが2桁でも気にすんな。
三平方の定理(ピタゴラスの定理)の公式にぶち込めばいいんだ。
x² = 5² + 12²
x = 13
直角三角形と言えども、いつも右下に直角が来るとは限らんぞ。
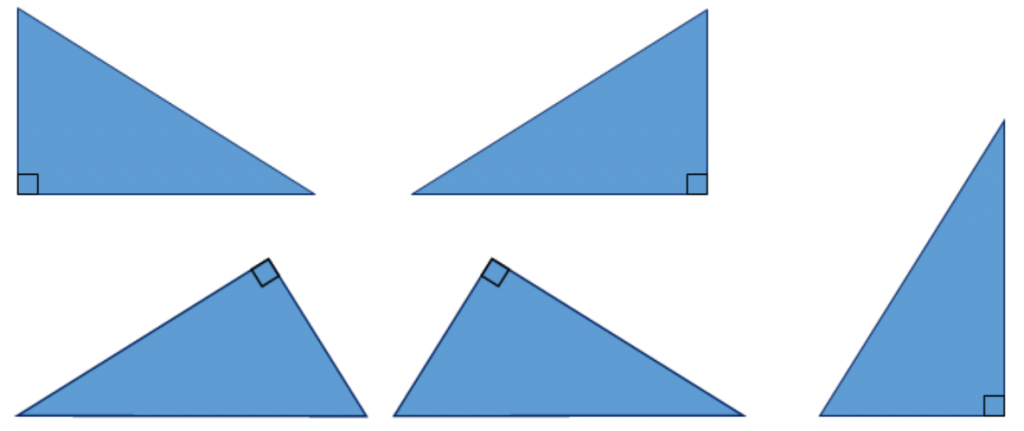
なっ。向きが変わると、斜辺がどれなのかうっかりしてしまうよ。
要注意だな。
Step2. 「平方根の計算混じってるタイプ」
2つ目のタイプは、
三平方の定理の計算に「平方根・ルートの計算」が混じってるやつだ。
たとえば、次のような練習問題。
練習問題2.
つぎの直角三角形の辺の長さxを求めてください。
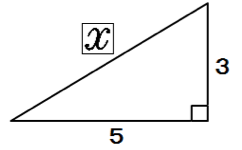
三平方の定理で直角三角形の辺の長さを計算してみると、
x² = 3² + 5²
x = √34
になるね。

答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。
Step3. ピタゴラスが悩んだ直角二等辺三角形
つぎは、直角二等辺三角形の辺の長さを三平方の定理で計算する問題。
たとえば、三平方の定理を発見したピタゴラスも悩んだと知られる次の問題だ。
練習問題3.つぎの直角三角形の辺の長さxを求めてください。
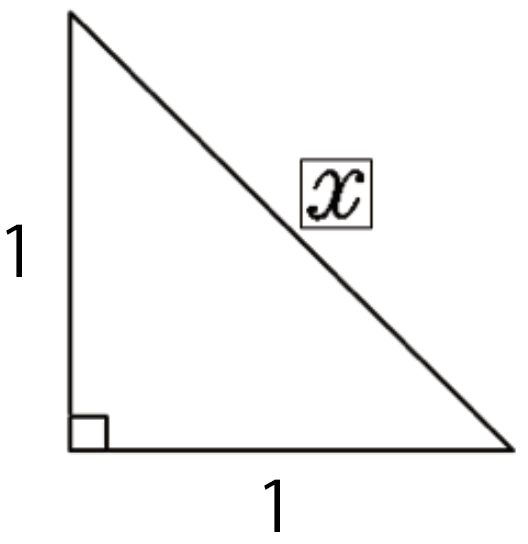
直角二等辺三角形だけど、さっきの計算問題と同じだ。
三平方の定理の公式を使ってやると、
x² = 1² + 1²
x = √2
になるぞ。
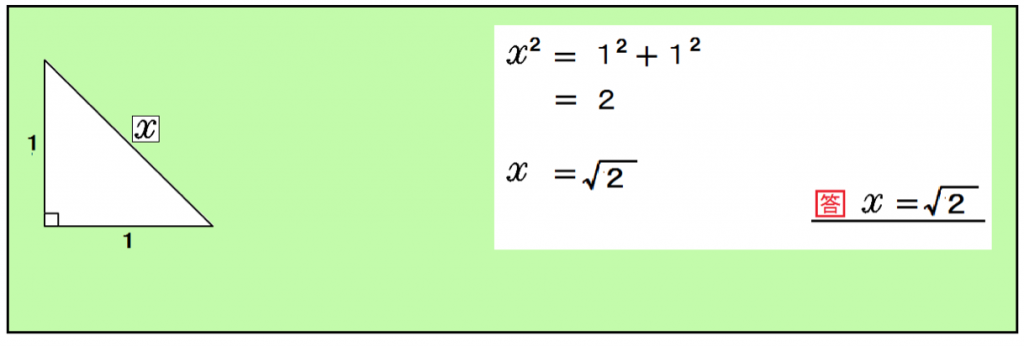
この直角二等辺三角形からピタゴラスは「無理数」を発見したと言われているんだ。
でも、ピタゴラスの生きてた時代は、まだまだ自然科学より宗教の勢力の方が主流でな。
ピタゴラス学派がうっかり、そして見事にピタゴラスの定理を見つけたんだが、
2乗して2になる数なんて、まだ見つかってなかった。
やや、これを発表したら、世の中大変なことになる・・・・
ってんで、長いこと秘密にしてたらしいぞ。

今は平和だ。
無理数はある!!と大声で言えるいい時代だ。(。)
問題4. 直角三角形が2つくっついてる問題
つぎは、
直角三角形が2つくっついてる問題な。
たとえば、次の練習問題だ。
練習問題4.
つぎの直角三角形の辺の長さxを求めてください。
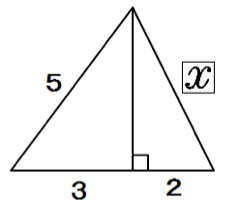
このタイプの問題では、高さを新しい文字で置いて2つの三角形の辺を出していくぞ。
まず、大きい三角形の高さをyとしてみよう。
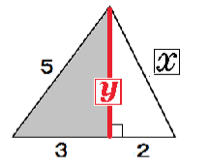
まず、灰色の直角三角形でyを計算してみる。
5² = 3² + y²
y = 4
そして、残りの白い直角三角形でxを出せばいいのさ。
x² = 4² + 2²
x = 2√5
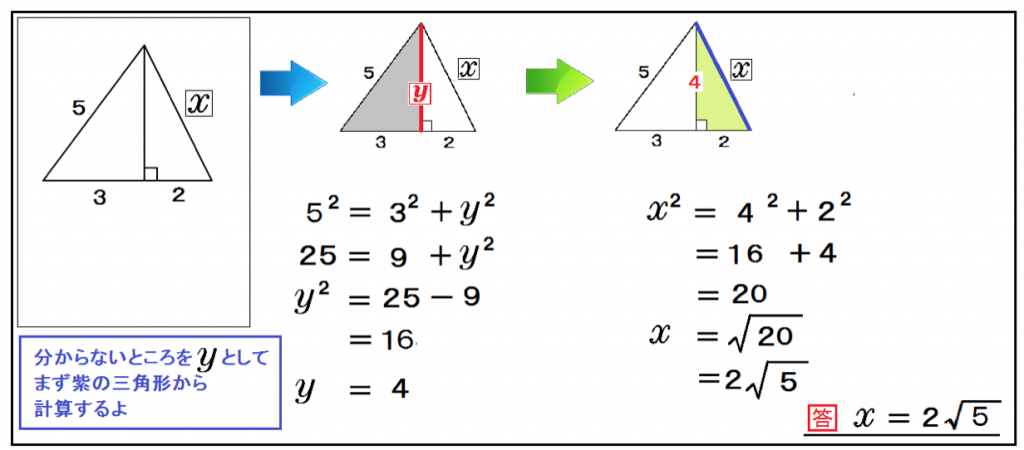
解き方大体わかっただろ??
じゃあつぎの計算問題にもチャレンジしよう。
練習問題5.
つぎの直角三角形の辺の長さxを求めてください。
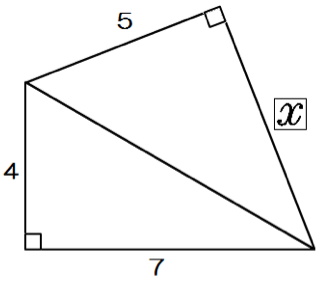
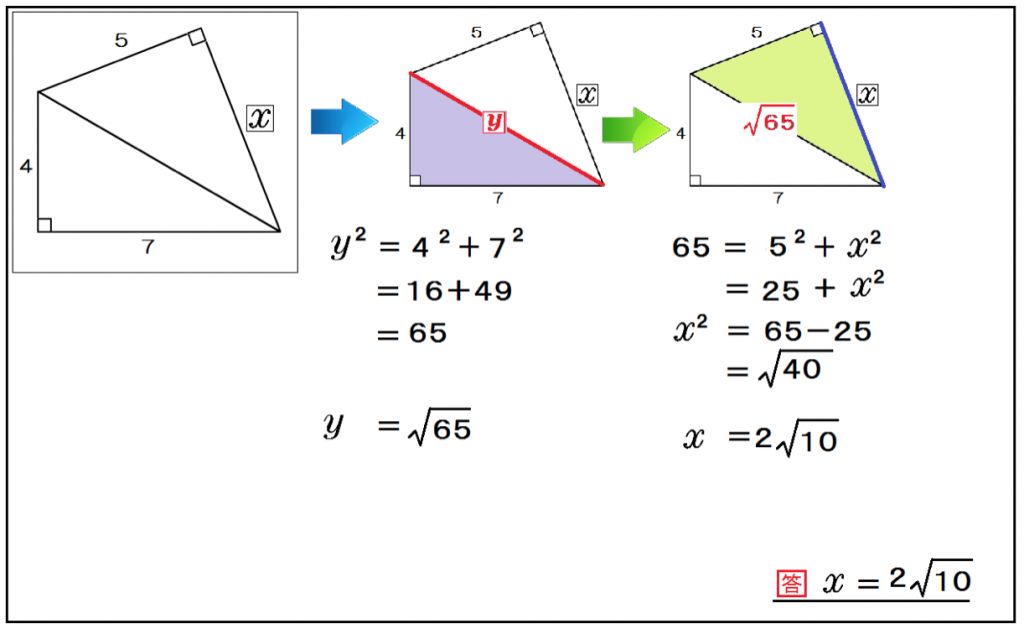
この問題も解き方はおんなじだ。
まず、真ん中の辺をyとして、yから計算すればいいんだね。
y² = 4² + 7²
y = √65
つぎはxを計算!
65 = 5² + x²
x = 2√10
まとめ:三平方の定理(ピタゴラスの定理)を使えば直角三角形の辺の長さは大体わかる!
三平方の定理で、直角三角形の辺の長さを求める問題はどうだった?
今日勉強した問題のパターンは4つだったな?
- 超基本タイプ
- 平方根の計算混じるタイプ
- 直角二等辺三角形
- 三角形が2つ合体タイプ
これだけの基本パターンやったら、少しは自信がついたな。
慣れるまではピタゴラスの定理の式に丁寧に数値を代入してくれ。


それじゃあな
Drリード


