多項式の計算問題を瞬殺したい！？
こんにちは！この記事をかいているKenだよ。焼き肉はうまいね。
中2数学のテストでいい点をとるためには、
いろいろな多項式の計算方法
をマスターしておくべきなんだ。
だって、中2数学の基礎的な内容だからね。
多項式の計算の攻略なしにして、中2数学の攻略なし、
ってわけさ。
今日はそんな中2数学のカギをにぎる「多項式の計算」の問題の解き方を
3ステップで紹介していくよ。
よかったら参考にしてみて。
多項式の計算問題を瞬殺できる3つのステップ
例題をときながら多項式の計算方法をみていこう！
例題：
つぎの計算をしなさい。
2(a+3b+c)-3(2a+5b+3)
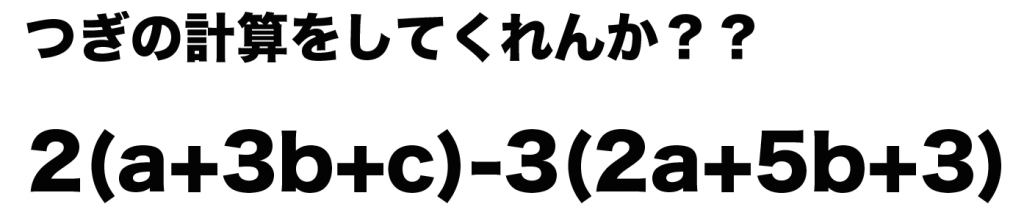
つぎの3ステップでいいんだ。
Step1. 分配法則で（）をはずす！！
分配法則をつかって多項式の（）をはずしちゃおう！
（）がついている多項式ってぽっちゃりしてるっしょ？
だから、こいつをスッキリさせちゃうってわけ。
例題の多項式も（）が2つあるよね。
この邪魔くさい（）を分配法則ではずしてやると、
2(a+3b+c)-3(2a+5b+3)
= 2a+6b+2c-6a-15b-9
になるね！
−の符号に注意しながら（）をはずしてみてね。
Step2. 同じ文字の項（同類項）をみつける！！
スッキリした多項式の中から、
同じ文字の項（同類項）
をみつけてみよう！
aが使われている項、bが使われている項・・・というように文字ごとに洗い出していけばいいんだ。
例題をみてみると、
分配法則でカンタンにした多項式（2a+6b+2c-6a-15b-9）には、
- a
- b
- c
- 数字
っていう4種類の項があるよね？？
こいつらがそれぞれ何個ずつあるかってことを押さえておこう！
- a（2つ）
- b（2つ）
- c（1つ）
- 数字（1つ）
Step3. 同類項の係数をたすっ！！
さっきみつけた「同じ文字の項（同類項）」の係数を足し合わせてみよう。
あ、係数って文字の前についている数字のことだよ。
例題の多項式では、
- a
- b
という2種類の文字が2つ以上ふくまれていたよね？
ってことはコイツらの係数を足してやればいいわけさ。
すると、
2a+6b+2c-6a-15b-9
= -4a -9b +2c -9
になるね！
これで多項式の計算は終了さ。おめでとう！！
まとめ：多項式の計算は「かけ算」から「たし算」へ
多項式の計算問題は、
- （）を分配法則ではずす
- 同類項をみつける
- 同類項をまとめる
っていう3ステップで攻略できちゃうんだ。
これさえ押さえておけば中2数学の基礎はできたようなもんさ。
テスト前にもう一度復習してみてね。
そんじゃねー
Ken
