多角形の外角の和ってどうなるの？？
こんにちは！この記事をかいているKenだよ。弾丸旅行にはまっているね。
180°×(n-2)
で計算できたね。
ここで、好奇心旺盛なヤツはこう思うはずだ。
そう。
そうだ。
多角形の外角の和はいくつになるんだろう！？？
ってね。
今日はそんな疑問にこたえるため、
多角形の外角の和の求め方をわかりやすく解説していくよ。
よかったら参考にしてみてね。
超簡単！多角形の外角の和は○○度！
結論からさきにいっちゃおう。
多角形の外角の和（n角形）はずばり、
360°
だ。
三角形の外角の和は360°。
四角形の外角の和も360°。
なんと、八十角形の外角の和も360°だ。。
いや、むしろ、
こんなんでも、
あんなんでも、
外角の和は360°になっちゃうんだ。
だから、
外角の和を求めなさい！
っていう問題がでたら、ドヤ顔で、
360°ですけどなにか？
っていってやろう。
なぜ多角形の外角の和が360°になるのか証明しよう！
多角形の外角の和は360°ってことはわかった。
むちゃくちゃわかりやすいね。
ただ、ここで知っておいてほしいのは、
なぜ多角形の外角の和が360°になるのか？？
ってことさ。
こいつを知っていると、
たぶん、
モテルね。
内角と外角をぜんぶたすといくつ？？
たとえば、
n角形があったとしよう。
1つの頂点に注目してみると、
「内角」と「外角」で1つの直線になっているよね？？
つまり、
内角 + 外角 = 180°
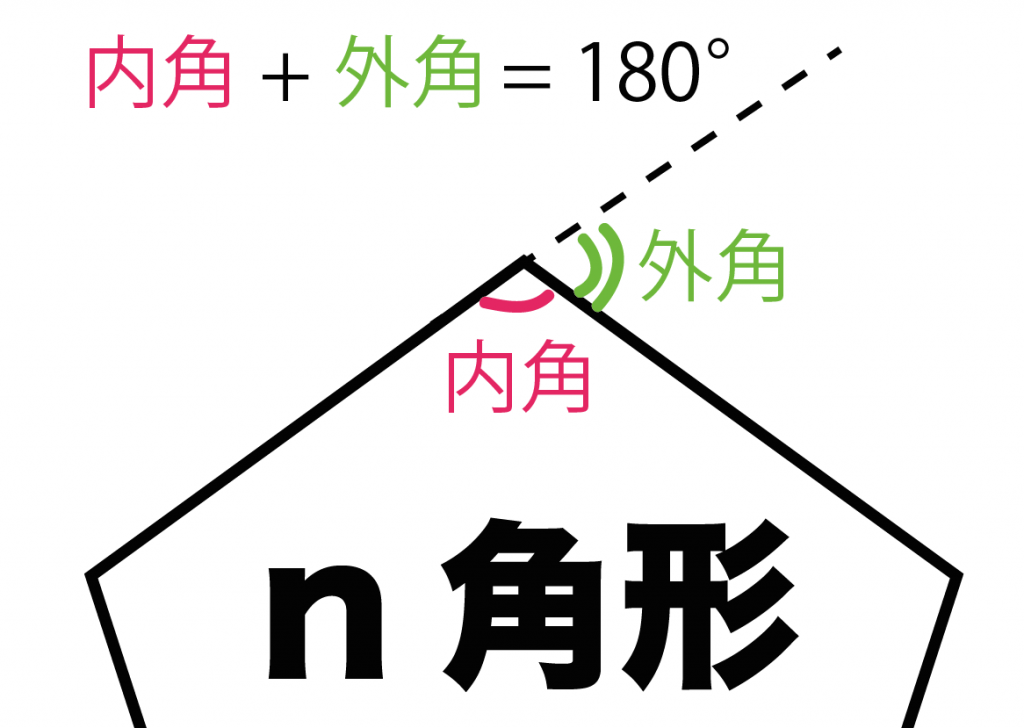
になっているってわけさ。
これは全頂点で同じことが言えるから、
内角と外角をぜーんぶ足し合わせたら、
180n
になるはずだ。
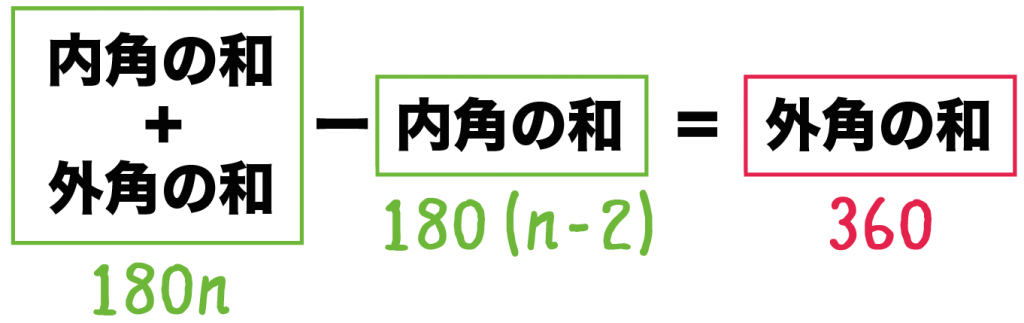
「内角と外角の和」から「内角の和」をひいてみる
「内角と外角の和」から「内角の和」をひいてやると、
「外角の和」になる。
多角形の内角の和（n角形）は、
180(n-2)
だったよね？？
よって、
（内角と外角の和）- （内角の和）
= 180n – 180(n-2)
= 360°
になるね。
つまり、
多角形の外角の和（n角形）は、
360°になるんだ！
この数字にはnがふくまれてないから、
何角形でも外角の和は360°になるんだ。
まとめ：多角形の外角の和は360°である。
多角形の外角の和はシンプル。
いつでも、
どんな多角形でも、
360°になるんだ。
テストで間違わないようにおぼえておこう！
そんじゃねー
Ken
