五角形の内角の和は何度？？
こんにちは！この記事をかいているKenだよ。チキン、うまいね。
五角形の内角の和って何度だろう？？
ときどき、そんなこと考えちゃうよね。
そんなときは、
多角形の内角の和の公式をつかえば大丈夫。
たぶん、3秒で計算できるよ。
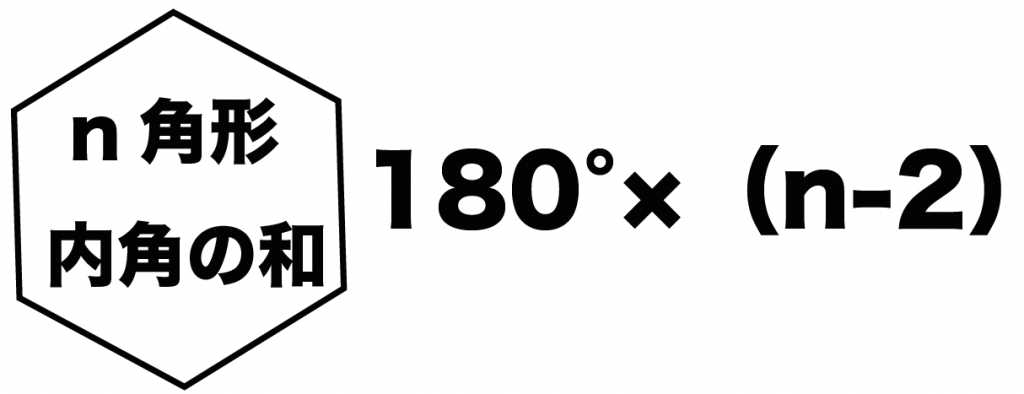
180°×（n-2）
っていう公式のnに「5」を代入してあげる。
すると、
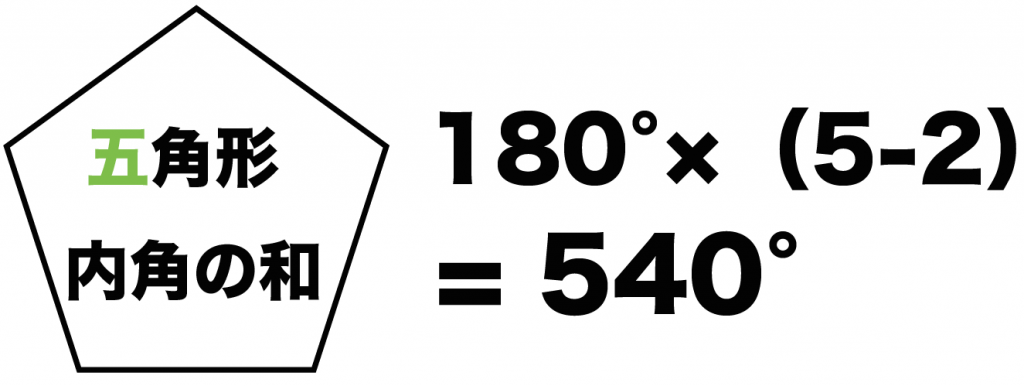
180°×（5-2）
= 540°
になる。
つまり、
五角形の内角の和は「540°」ってことさ！
なんで内角の和が540°になの？？
公式をつかえば1秒ぐらいで計算できそうだけど、
そもそもなんで「540°」になってるんだろう？？
チョー気になるよね。
その理由は、
五角形の中に三角形が3つも潜んでいるからなんだ。
まず、
対角線を2本ひいてみよう。
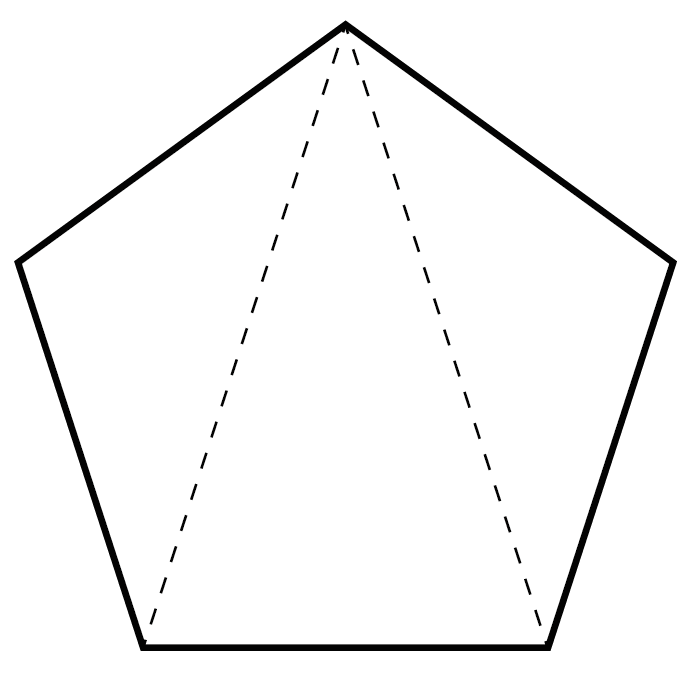
すると、どうだろう？？
三角形が3つも隠れていることがわかるよね。
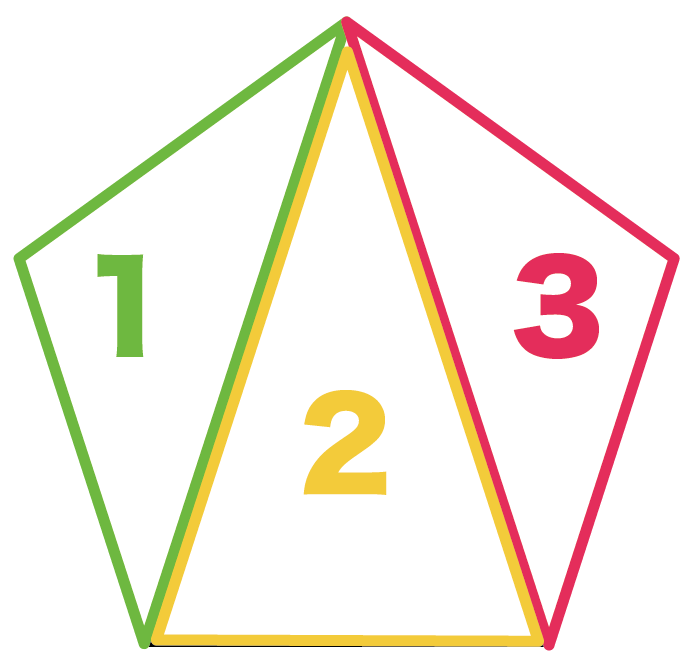
三角形の内角の和は「180°」で、5角形には三角形が3つもかくれているんだ。
よって、
五角形の内角の和は「三角形の内角の和（180°）」を3倍した
180°×3
= 540°
になるのさ。
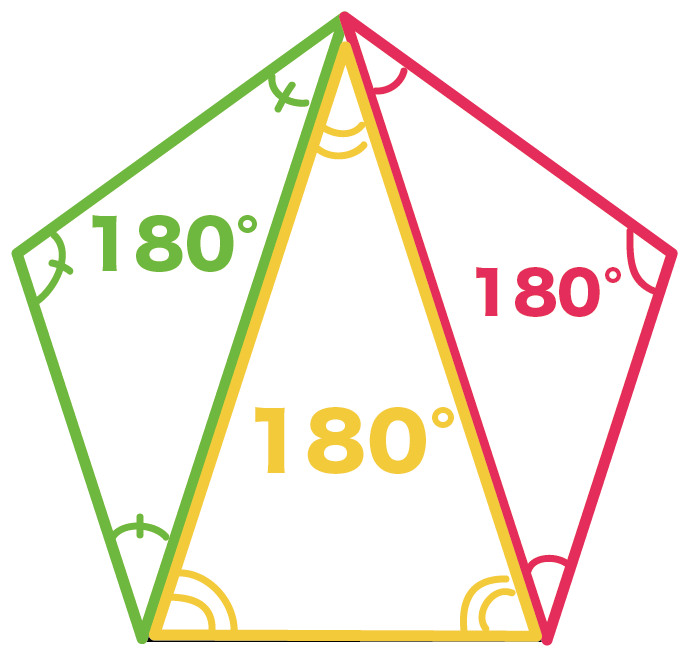
まとめ：5角形には三角形が3つ入っている！
五角形の内角の和を求めるときは、
180°×（n-2）
のnに5を代入しよう。
テストにでやすいから復習しておいてね。
そんじゃねー
Ken
