【中2数学】平行四辺形の性質がわかる3つの証明
平行四辺形の性質の証明がよくわからん??
こんにちは!この記事をかいているKenだよ。パイナップルに埋もれたい。
平行四辺形の性質には次の3つがあったよね。
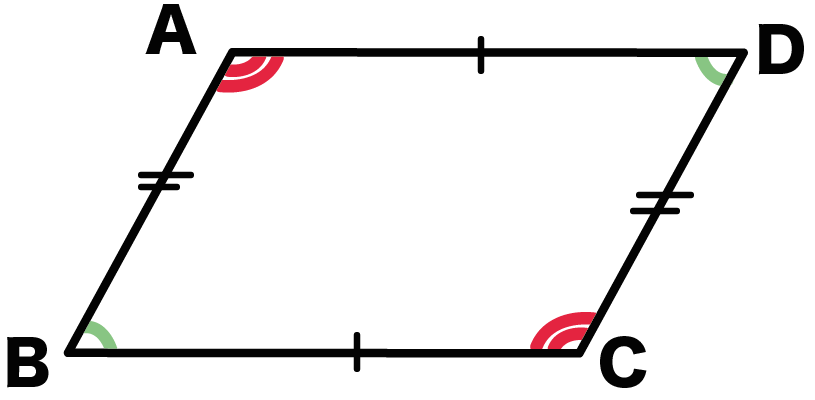
- 2組の向かいあう辺はそれぞれ等しい
- 2組の向かいあう角はそれぞれ等しい
- 対角線はそれぞれ中点で交わる
こいつらはむちゃ便利だ。
だって、
「平行四辺形」だったら、
向かいあう辺・角が等しいっていえちゃうんだからね。
しかも、対角線が中点でまじわるんだって。
こいつらを使えば、
平行四辺形の問題なんて瞬殺さ!
もー、最高だね・・・・・・
だがしかし。
なんで「平行四辺形の性質」って使えるんだろう??
便利すぎて怪しい。
詐欺かって思うよね??
そこで今日は、
平行四辺形の性質の証明を解説して、
疑問を解消していこう!
平行四辺形の性質がわかる3つの証明
平行四辺形の性質を証明するには、
三角形の合同をつかうよ。
しかも、3組の合同を証明しなくちゃいけないんだ。
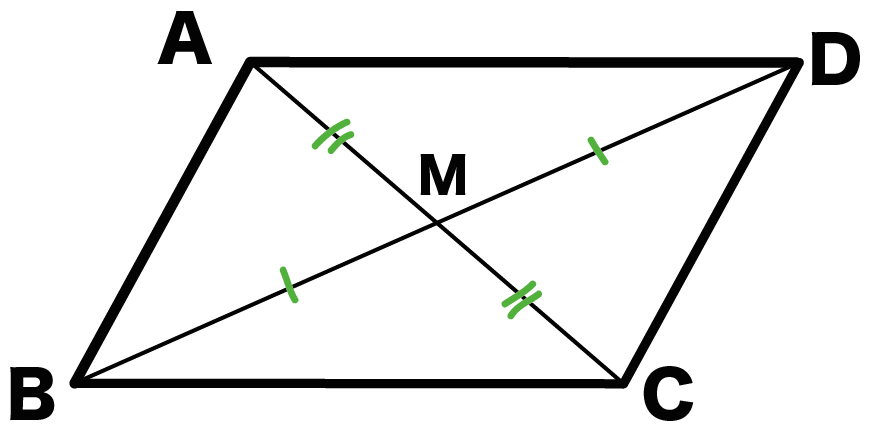
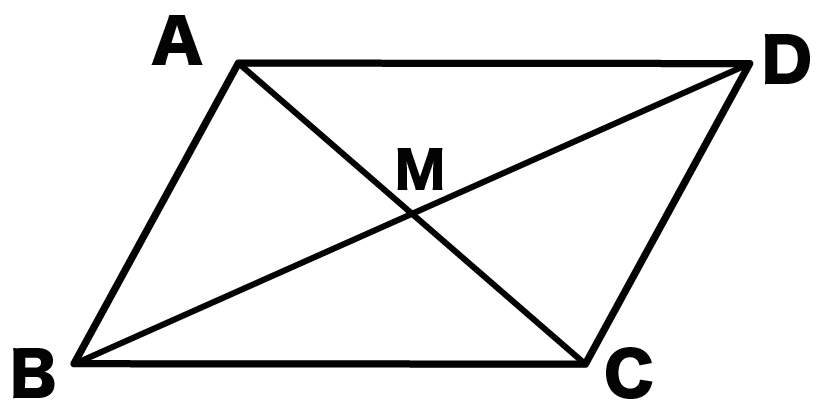
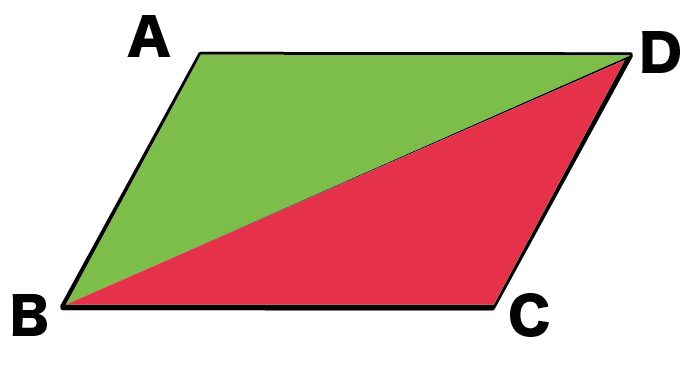
平行四辺形ABCDがあって、
対角線の交点をMとしよう。
このとき、△ABCと△ADCと、
△ABDと△CDB、
△ABMとCDMの合同を、
を証明していくんだ。
こいつらの合同がいえれば、
平行四辺形の性質を証明できるってわけ。
順番にみていくよー
証明1. 「2組の向かい合う辺の長さは等しい」
まずは、平行四辺形の性質の、
2組の向かいあう辺の長さは等しい
を証明していこう。
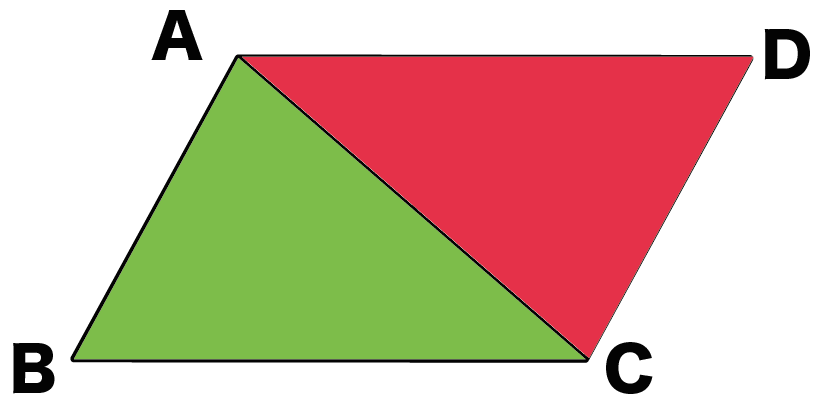
- △ABC
- △CDA
の三角形の合同を証明していくよ!
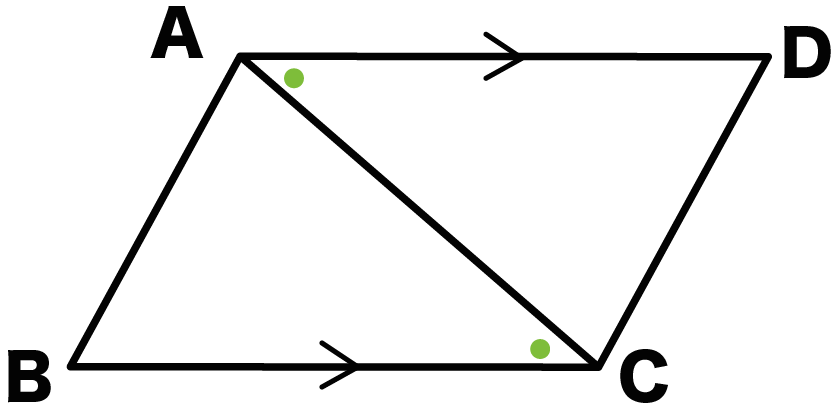
△ABCと△CDAにおいて、
四角形ABCDは平行四辺形だから、
AD // BC・・・・(1)
だね。
平行線の性質より錯角が等しいから、
角ACB = 角CAD・・・・(2)
になる。
同じように、
AB // CDより、
錯角が等しいから、
角BAC = 角DCA・・・・(3)
んで、
辺ACは共通だから、
AC = CA ・・・・・(4)
になるね。
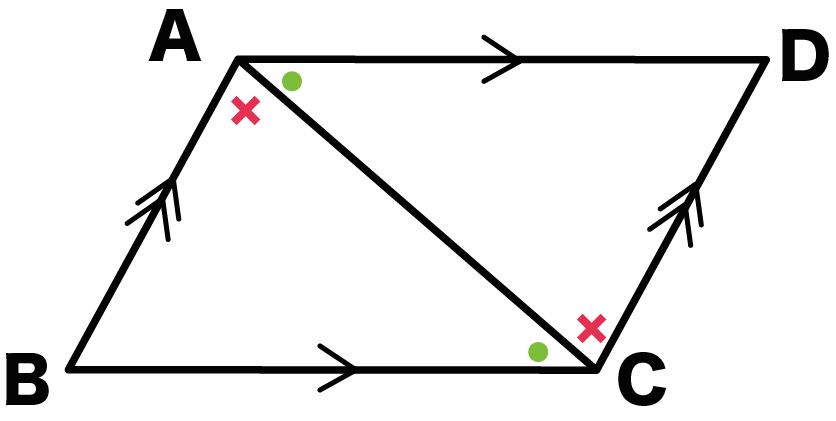
(2)、(3)、(4)より、
1組の辺とその両端の角がそれぞれ等しいから、
△ABC ≡ △CDA
になるね。
また、
対応する辺の長さが等しいから、
- AB = CD
- BC = DA
になる。
これで、平行四辺形の性質の、
「2組の辺の長さがそれぞれ等しい」
ってやつが証明できた。
証明2. 「2組の向かい合う角の大きさがそれぞれ等しい」
つぎは2つめの、
2組の向かいあう角の大きさがそれぞれ等しい
の証明だ。
さっき証明した、
△ABC ≡ △CDA
をつかおう。
対応する角がそれぞれ等しいから、
角ABC = 角CDA・・・・(5)
ってことがいえる。
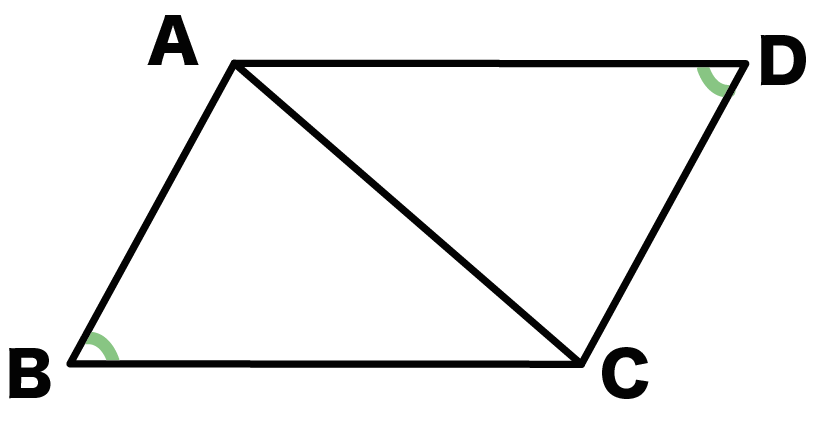
△ABC と△CDAおなじように、
△ADCと△CBAの合同
も証明できる。※ここでは省略するね。
こいつらでも対応する角が等しいから、
角BAD = 角BCD・・・・(6)
ってことがいえるんだ。
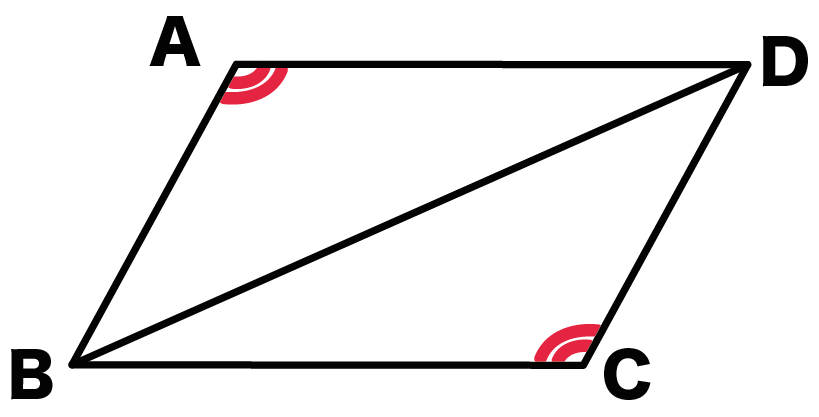
(5)・(6)より、
- 角A = 角C
- 角B = 角D
がいえる。
よって、
2組の向かいあう角の大きさがそれぞれ等しい
っていう性質を証明できるんだ。
証明3. 「対角線は中点でまじわる」の証明
最後は、
対角線はそれぞれの中点で交わる
という性質を証明していくよ。
ここでは、
△ABMと△CMDの合同
を証明していくんだ。
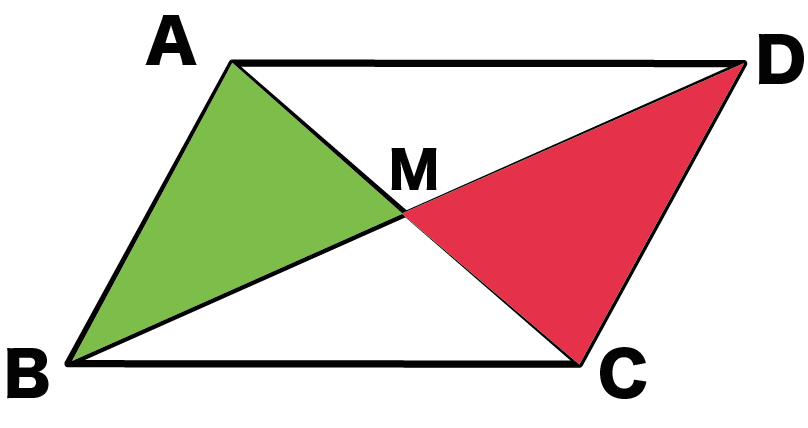
△ABMと△CMDにおいて、
さっき証明した、
「2組のむかい辺はそれぞれ等しい」
っていう性質をつかうと、
AB = CD ・・・・(1)
ってことがわかる。
AB//CDより、錯角が等しいから、
角BAM = 角DCM・・・・(2)
角ABM = 角CDM・・・・(3)
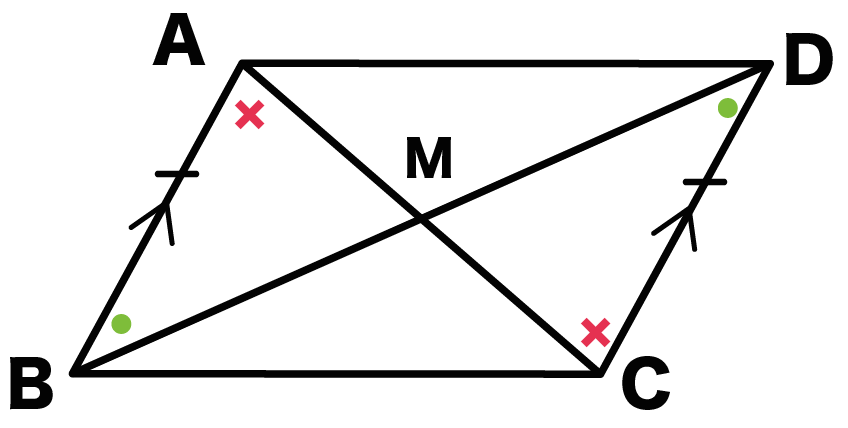
(1)、(2)、(3)より、
1組の辺とその両端の角がそれぞれ等しいから、
△ABM ≡ △CDM
になる。
よって、
対応する辺はそれぞれ等しいから、
- AM = CM
- BM = DM
になるよー!
つまり、
平行四辺形の対角線は中点で交わるんだ。
おめでとう!
平行四辺形の性質を3つ証明できたね。
まとめ:平行四辺形の性質は三角形の合同の証明から!
平行四辺形の性質の証明はシンプル。
ぜーんぶ、
三角形の合同
からきているんだ。
合同な図形をしっかり見極めて、
ゆっくり証明していこう。
そんじゃねー
Ken