【中2数学】平行四辺形の3つの性質
平行四辺形の性質ってなに??
こんにちは!この記事をかいているKenだよ。故郷が恋しいね。
平行四辺形の定義はわかった。
だけど、
平行四辺形にはどんな性質があるんだろう??
って思うよね。
今日はそんなときに備えて、
平行四辺形の性質を3つ紹介していくよ。
よかったら参考にしてみて。
おさえておきたい!平行四辺形の3つの性質
平行四辺形の性質には3つあるんだ。
- 2組の向かいあう辺は、それぞれ等しい
- 2組の向かいあう角は、それぞれ等しい
- 対角線はそれぞれの中点で交わる
うえからみていくよー!
性質1. 「2組の向かい合う辺はそれぞれ等しい」
1つ目の性質は、
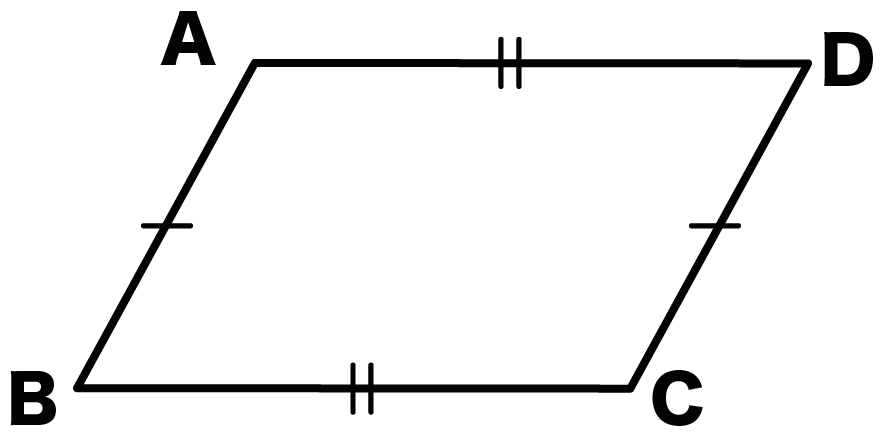
2組の向かいあう辺はそれぞれ等しい
というものさ。
平行四辺形ABCDがあったしよう。
向かいあう辺どうしが等しいから、
- AB = CD
- AD = BC
になるんだ。
つまり、
平行四辺形の1辺がわかると、向かいあった辺の長さもわかる
ってことなんだ。
すごくない??
たとえば、
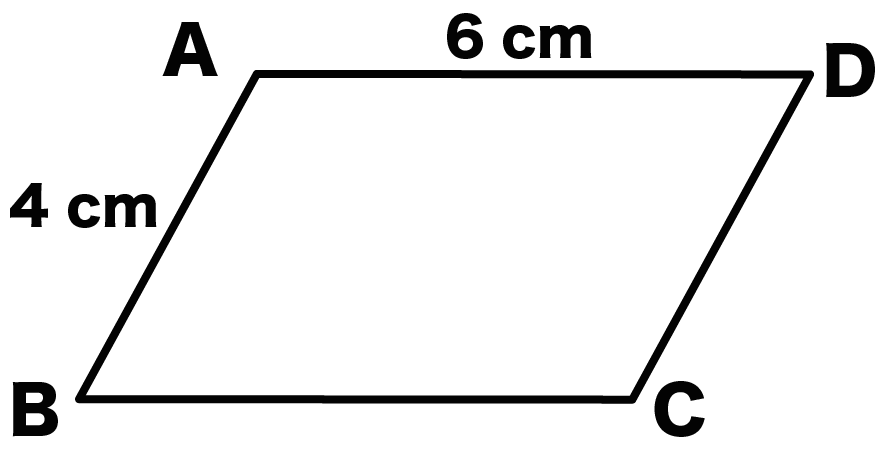
- AB= CD = 4 cm
- AD = BC = 6 cm
だったとしよう。
残りの辺の長さを求めてみよう。
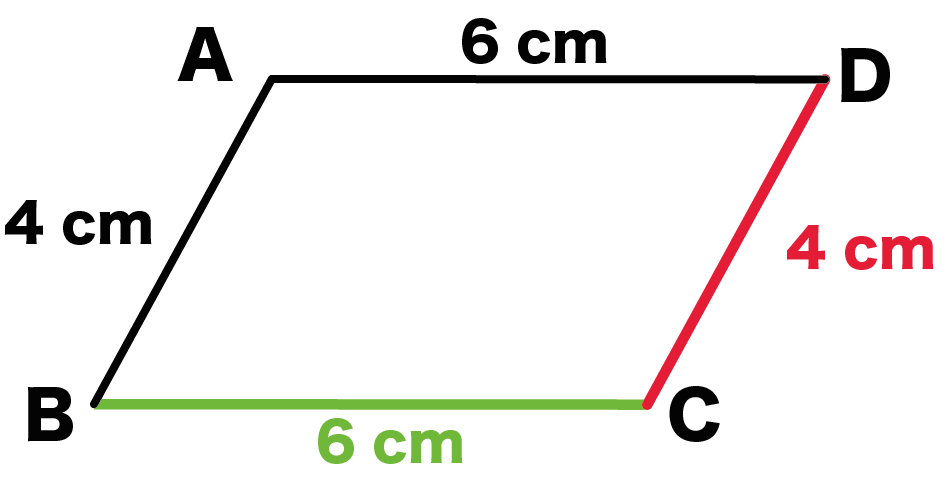
2組の向かいあう辺の長さは等しいので、
- BC = 6 cm
- CD = 4 cm
になるんだ。
どう?
クソ便利な性質でしょ??。
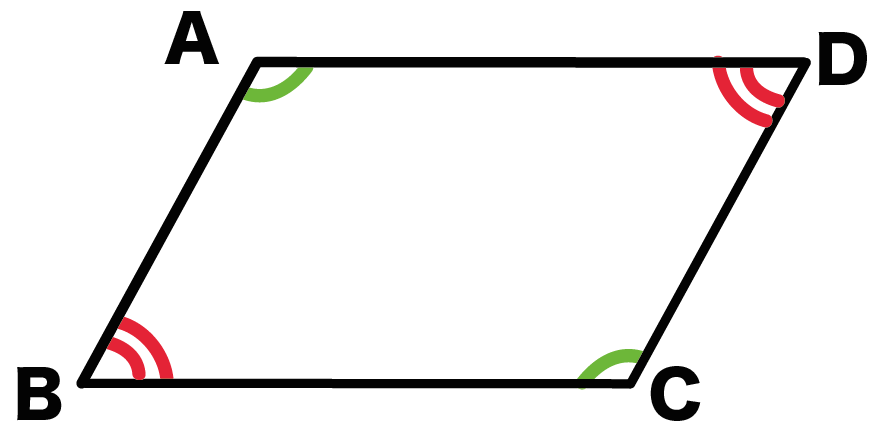
性質2. 「2組の向かいあう角はそれぞれ等しい」
つぎは角度についての性質。
2組の向かいあう角はそれぞれ等しい
というものがあるんだ。
平行四辺形ABCDがあったとしよう。
向かいあう角が等しいから、
- 角A = 角C
- 角B = 角D
になるんだ。
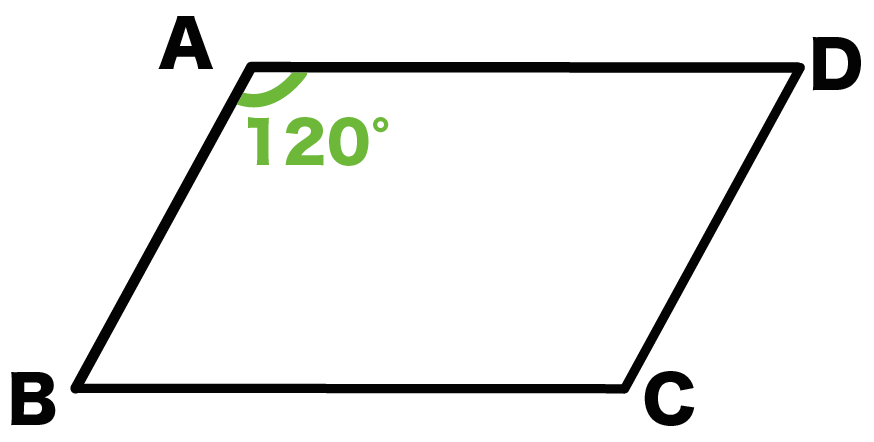
たとえば、角A = 120°だとしたら、
角C = 120°になるってこと。
しかも、
角B = 角Dってことを使えば、
残りの角の大きさもわかっちゃう。
角Bと角Dの大きさは、
(四角形の内角の和 360°)から
(角AとCをひいたもの)を(2でわったやつ)になる。
角B = 角C = (360-120-120)/2
= 60°
になるってことだ。
1つの角度がわかれば、ぜーんぶの角度がわかっちゃうんだよ。
すごいね!
性質3.「対角線はそれぞれの中点で交わる」
いよいよ最後の性質だ。
平行四辺形の対角線は中点で交わる
ってやつだよ。
平行四辺形ABCDがあったとしたら、
対角線ACとBDは中点でまじわっているんだ。
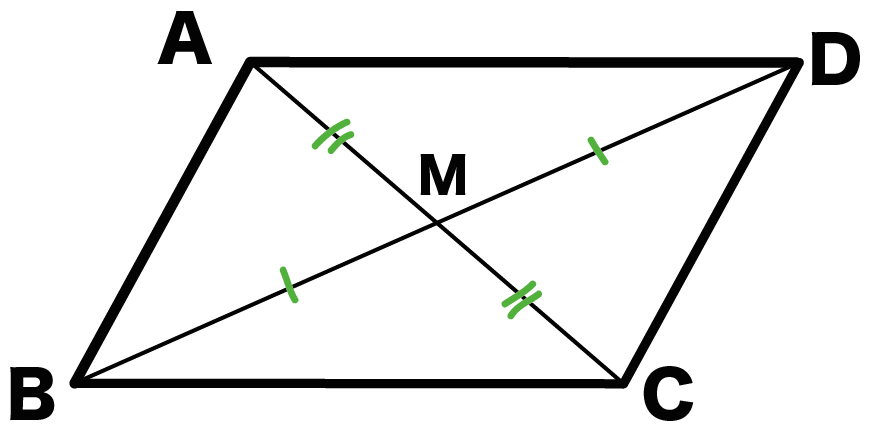
対角線の交点をMとすれば、
- AM = CM
- BM = DM
になってるってことさ。
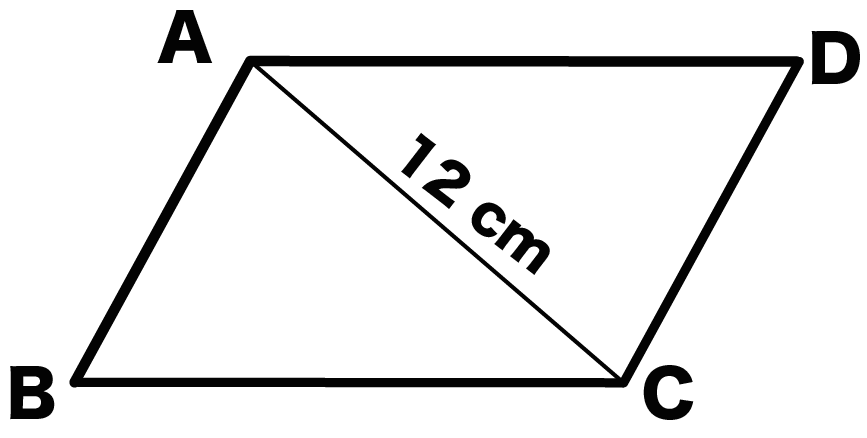
たとえば、対角線ACの長さを12cmとしよう。
気分で、
もう1つ対角線BDをひいたとしよう。
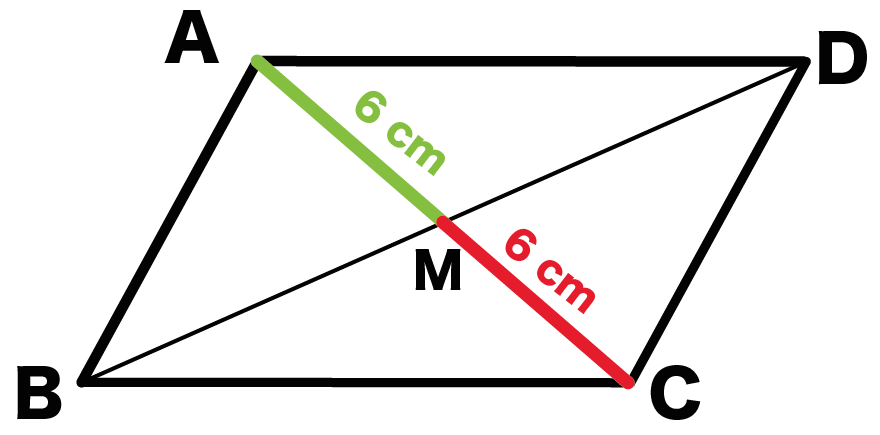
交点をMとすると、
AM = CM = 6 cm
になっちゃうんだ。
つまり、
対角線ACの中点で、
ACとBDがまじわっているわけだね。
これで平行四辺形の3つの性質はおわり!
ゆっくりでいいからおぼえていこう。
まとめ:平行四辺形の3つの性質は辺・角・対角線について!
平行四辺形の3つの性質はどうだった??
- 2組の向かいあう辺は、それぞれ等しい
- 2組の向かいあう角は、それぞれ等しい
- 対角線は、それぞれの中点で交わる
こいつらは意外と問題にでてくる。
テスト前にしっかりとおさえておこう!
そんじゃねー
Ken