中学生ならおぼえたい!平行四辺形になる5つの条件
四角形が「平行四辺形になる条件」ってなに??
こんにちは!この記事をかいているKenだよ。トースターに注意だね。
ある日、ある町で、
とある四角形に出会ったとしよう。
初めて会ったから、顔も名前も知らない。
どんな性質をもっているかわからない。
謎が多すぎるってわけ。
でも、数学を勉強している中学生ならふと、あることが気になりだす。
それは、
この四角形が平行四辺形かどうか???
だ。
こいつが平行四辺形ってことがわかれば、
親近感もわく。近づきやすくなるかもしれない。
いや、もしかしたら親友になれるかもしれない。
このように、
ある四角形が「平行四辺形かどうか」を判断するときにつかうのが、
平行四辺形になる条件
なんだ。
ぜんぶで5つあるんだけど、今日はぜんぶ紹介していくよ。
よかったら参考にしてみて。
おぼえておきたい!平行四辺形になる5つの条件
平行四辺形の条件はぜんぶで5つある。
- 「2組の向かいあう辺が、それぞれ平行であるとき」
- 「2組の向かいあう辺が、それぞれ等しいとき」
- 「2組の向かいあう角が、それぞれ等しいとき」
- 「対角線が、それぞれの中点で交わるとき」
- 「1組の向かいあう辺が、等しくて平行であるとき」
どれか1つをみたしていれば、
その四角形は「平行四辺形」なんだ。
えっ。
5つも多すぎておぼえられないって!??
そうだね。
でも安心して。
この5つの条件のうち、4つはみたことがあるやつでしょ??
そう。
1つめが「平行四辺形の定義」の逆で、
2~4つめが「平行四辺形の性質」の逆なんだ。
つまり、
定義と性質をおぼえていれば、条件を4つおぼえたことになる。
あとは最後の、
「1組の向かいあう辺が、等しくて平行であるとき」
だけ暗記すればいいんだ。
念のために今日は、
条件を1から振り返っていくよ。
条件1. 「2組の向かいあう辺が、それぞれ平行であるとき」
1つめの条件は、
2組の向かいあう辺がそれぞれ平行であるとき
だ。
たとえば、ここに、
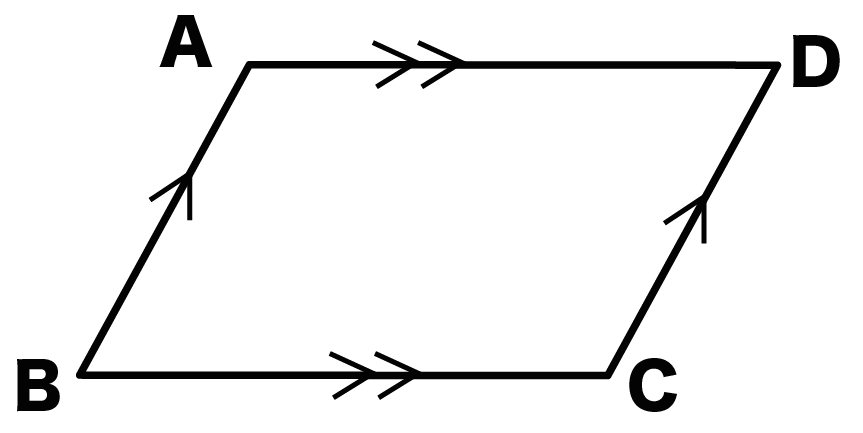
- AB // CD
- AD // BC
の平行四辺形ABCDがあったとしよう。
この四角形ABCDはなんと、
平行四辺形なんだ。
だって、
2組の向かいあう辺(ABとCD、ADとBC)が平行だからね。
平行四辺形の定義をみたす四角形は「平行四辺形」である
ってことをおぼえておこう。
条件2. 「2組の向かいあう辺が、それぞれ等しいとき」
つぎの条件は、
2組の向かいあう辺がそれぞれ等しいとき
だ。
これは平行四辺形の性質の逆をいっているね。
たとえば、四辺形ABCDの各辺が、
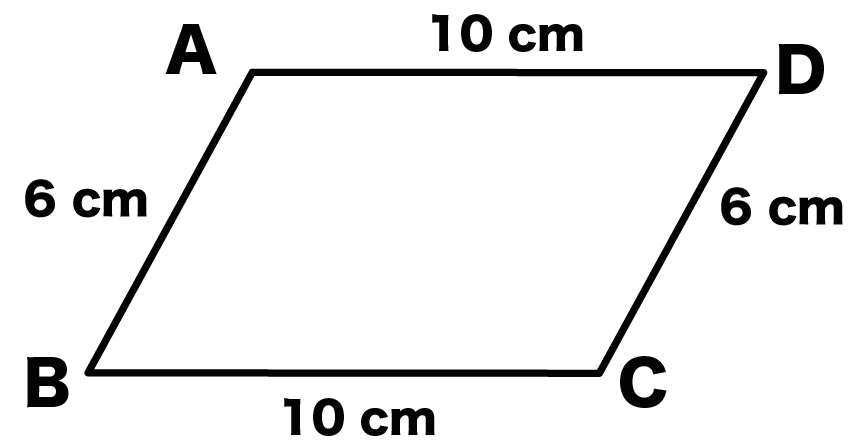
- AB = CD = 6cm
- AD = BC = 10 cm
だったとしよう。
こいつは、
2組の向かいあっている辺が等しい
という条件をみたしている。
よって、
四角形ABCDは平行四辺形なんだ。
条件3. 「2組の向かいあう角が、それぞれ等しいとき」
つぎは、
2組の向かいあう角が等しい
っていう条件だ。
これも平行四辺形の性質の逆をいっている。
たとえば、四角形ABCDのそれぞれの角が、
- 角A = 角C = 120°
- 角B = 角D = 60°
だったとしよう。
このとき、
向かいあう角同士が等しいから、
四角形ABCDは平行四辺形である
っていえるんだ。
条件4. 「対角線が、それぞれの中点で交わるとき」
4つめは、
四角形の対角線が中点でまじわっているとき
だ。
これも平行四辺形の性質の逆さ。
たとえば、
四角形ABCDの対角線を2本ひいたとき、
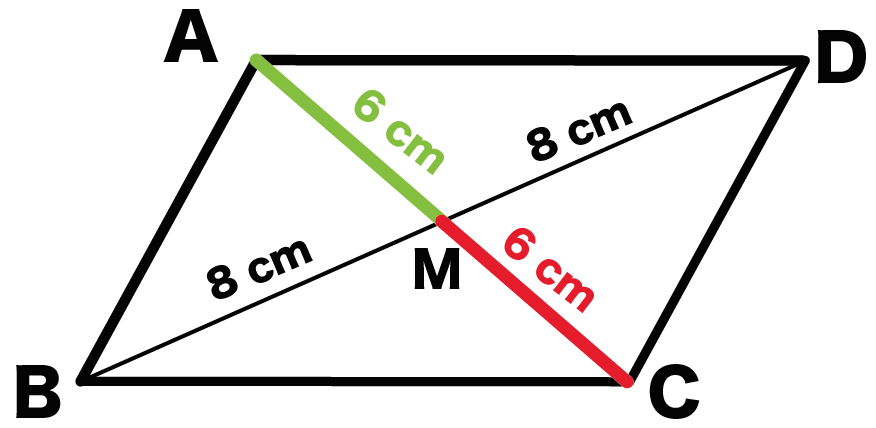
対角線ACとBDがMでまじわっているとしよう。
このとき、もし、
- AM = CM = 6 cm
- BM = DM = 8 cm
だったら、
四角形ABCDは「平行四辺形である」
っていえるんだ。
条件5. 「1組の向かいあう辺が、等しくて平行であるとき」
いよいよ最後の条件。
1組の向かいあう辺が等しく平行であるとき
だ。
これは平行四辺形の定義・性質の逆でもない。
オリジナルな条件なんだ。
ぶっちゃけ、
この条件さえおぼえておけば問題ない。
だって、あとは定義と性質の逆をいっているだけだからね。
たとえば、四角形ABCDで、
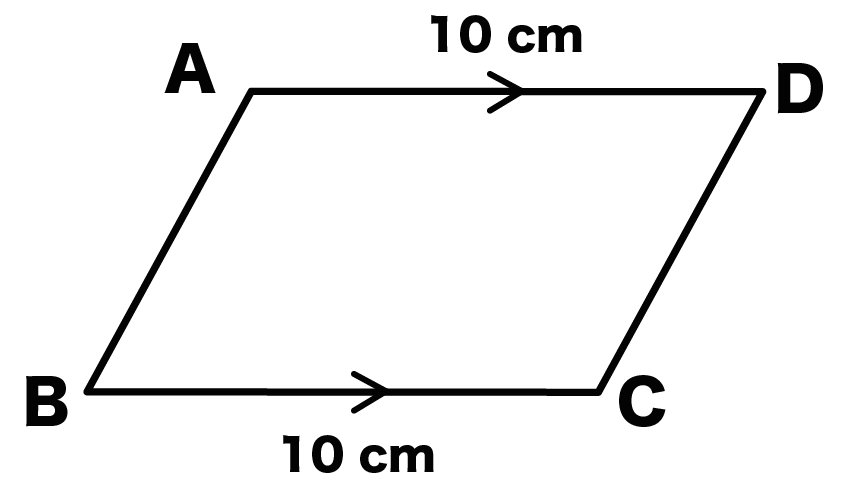
- AD = BC = 10 cm
- AD // BC
だったとしよう。
このとき、
1組の向かいあう辺が等しく平行である(ADとBC)
っていう条件をみたしている。
よって、
四角形ABCDは平行四辺形である
っていえるんだ!!
まとめ:平行四辺形になる条件は5つめが超重要!
以上が「平行四辺形になる条件」だよ。
とくに最後の、
1組の向かいあう辺が等しく平行である
ってやつがむちゃ重要。
なぜなら、
平行四辺形の定義・性質の逆じゃないからね。
メンドイときは最後の条件だけおぼえよう。
そんじゃねー
Ken