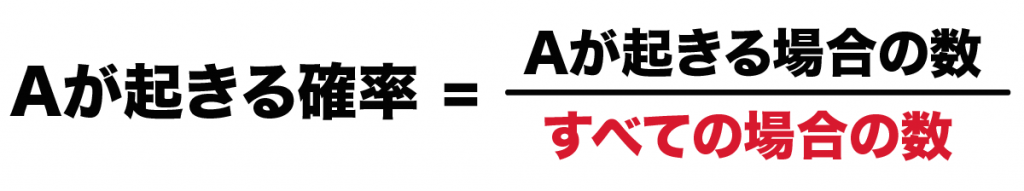【中学数学】場合の数がわかる2つの調べ方
場合の数の調べ方がわからない!
こんにちは!この記事をかいているKenだよ。散歩は大事だね。
中学数学の確率で重要なのは、
場合の数の調べ方
だ。
「場合の数」さえ数えられれば大丈夫。
あとは確率の公式にいれるだけだからね。
「場合の数の調べ方」さえおぼえれば、
確率マスターになれるわけさ。
今日はそんな確率で大切な、
場合の数の調べ方を2つ紹介するよ。
よかったら参考にしてみて。
確率で役立つ場合の数の調べ方2つ
中学数学ではおもに、
樹形図で場合の数を調べていくよ。
調べ方はつぎの2つさ。
- すべての場合の数の調べ方
- あるできごとの場合の数の調べ方
つぎの例題をときながら解説していくよ。
例題
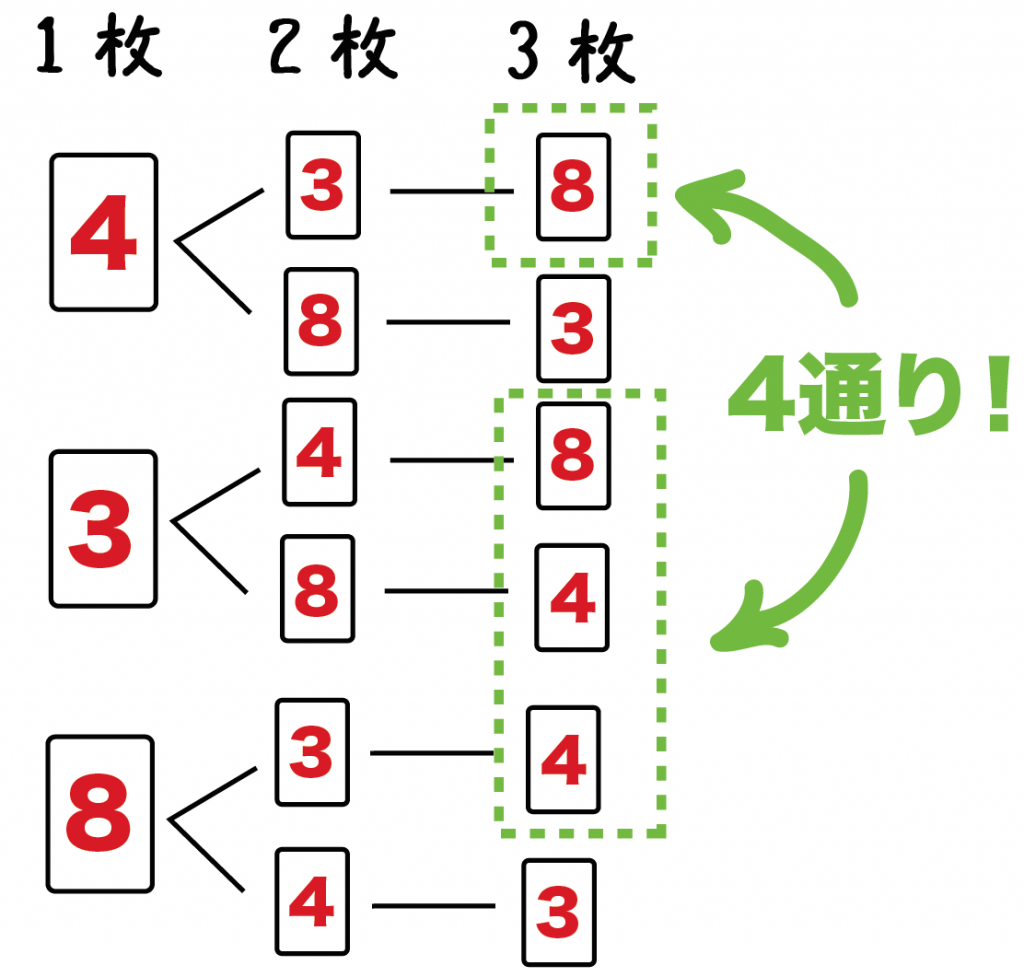
3・4・8がかかれたカードが3枚ある。こいつらを並べて3ケタの数字をつくるとき、偶数になる確率を求めよ。
このとき、樹形図はつぎのようになるね。
※詳しくは「樹形図の書き方」をよんでみてー!
調べ方1. すべての場合の数の調べ方
まずは「すべての場合の数」をしらべよう。
これは確率の計算で分母にくるやつだね。
調べ方はとっても簡単。
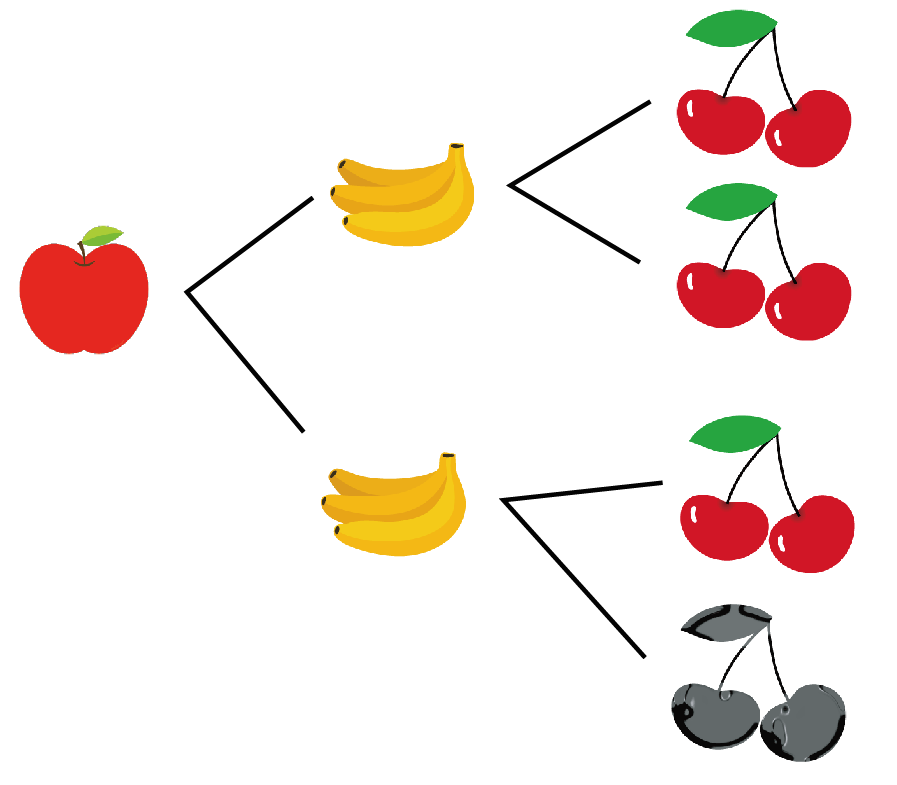
樹形図のいちばん右をぜんぶ数えればいいんだ。
例題でいうと、いちばん右には6つの実がなっているよね??
だから、
すべての場合の数は「6通り」になるんだ。
樹形図のいちばん右をかぞえると「すべての場合の数」になる
って覚えておこう。
調べ方2. 「あるできごと」の場合の数の調べ方
今度は「あるできごと」の「場合の数の調べ方」だね。
これは確率の公式の分子にくるやつだ。
この調べ方はちょっとむずかしい。
なぜなら、あてはまる場合の数を樹形図から選ばないといけないからね。
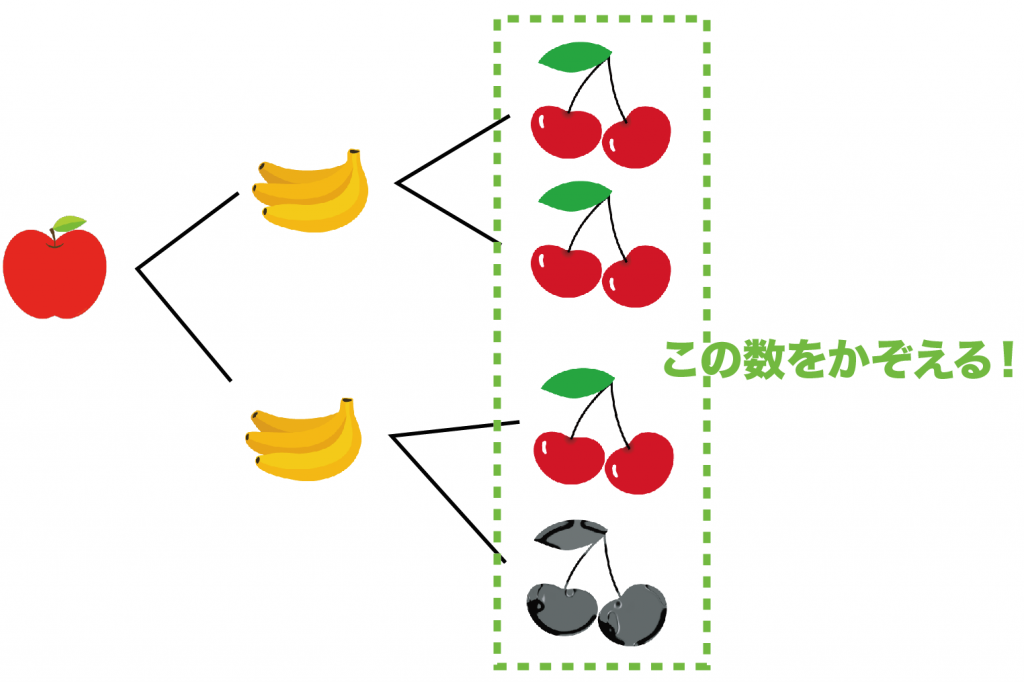
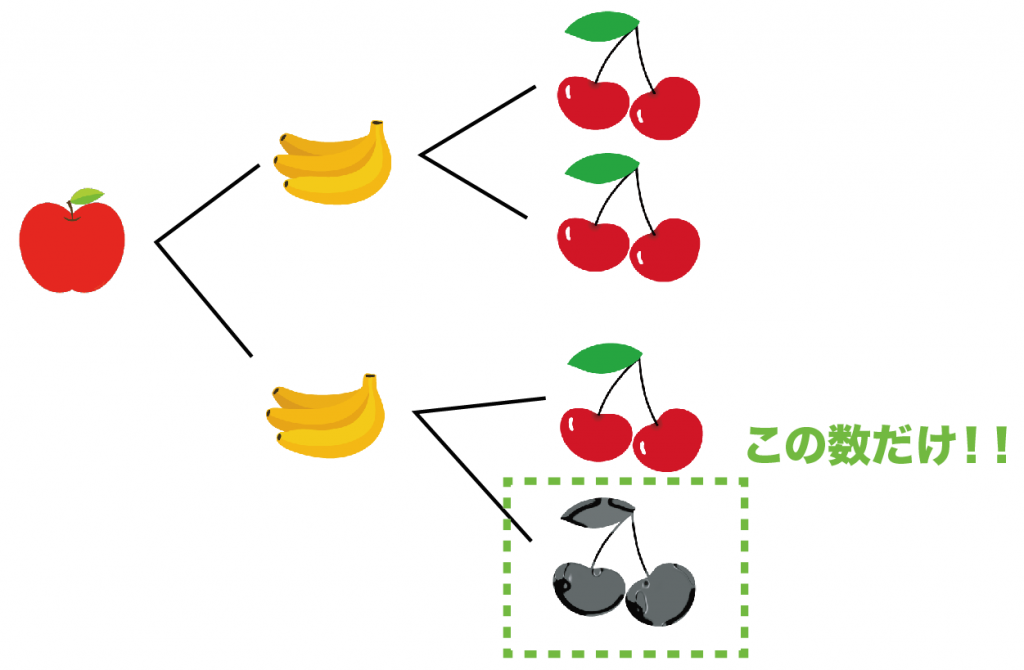
たとえば、さくらんぼが腐ってる場合の数をしらべたいとき。
このとき、樹形図をばーーってみてみよう。
さくらんぼが腐ってそうな場合の数をみつけるんだ。
ざっと見た結果、
緑でかこった1通りしかないね。
こんな感じで場合の数を数えればいいんだよ。
例題をみてみよう。
例題で求めたいのは、
3ケタの数字が偶数になる確率
だったよね??
樹形図でかぞえてみると、
4通りある!
よって、
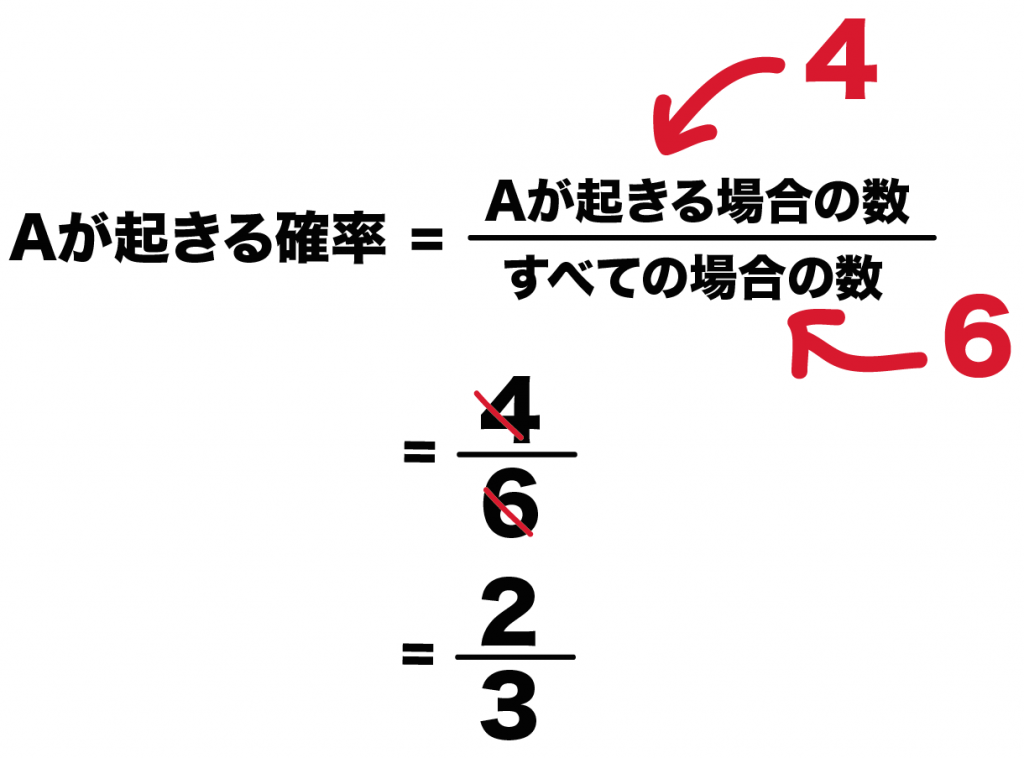
(3ケタの数字が偶数になる確率)
= (偶数になる場合の数)÷(すべての場合の数)
= 4÷6 = 2/3
になるね。
おめでとう!
これで場合の数の調べ方をマスターしたね。
まとめ:場合の数は樹形図と根性で調べよう!
中学数学では基本的に、
樹形図で場合の数をしらべていくよ。
- すべての場合の数
- あるできごとの場合の数
の2つさえ調べられればこっちのもの。
あとは、公式で確率を計算するだけだね。
じゃんじゃん調べていこう!
そんじゃねー
Ken