【一次関数の利用】2つの動点が台形上を移動する問題
「一次関数の利用」で必ず出てくるのが、
点が動く問題。
ちまたでは、
動点の問題
と呼ばれているやつだ。
一番テストに出てくるのは「1つの点が動くパターン」。
だけど、厄介なことに、たまーに、
「2つの点が動く」問題が出ることもある。
例えば次のような問題さ。
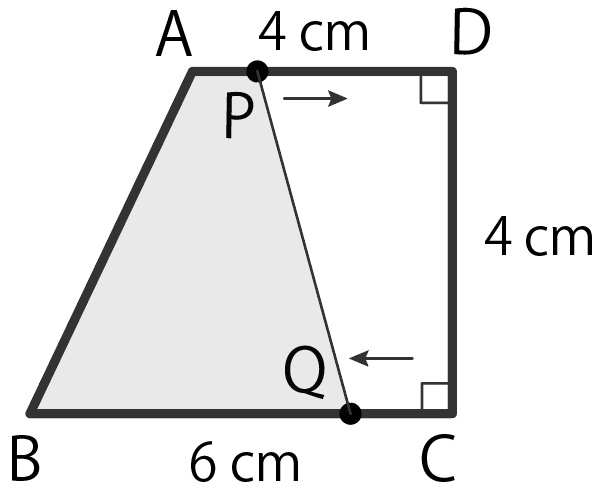
AD = 4 cm、BC = 6 cm、 CD = 4 cm、∠C = ∠D = 90°の台形ABCDがある。
2点P、QはそれぞれA、Cを同時に出発し、点Pは辺AD上を、点Qは辺BC上をどちらも毎秒 1 cmの速さで動く。
端まで行けば折り返し、12秒間動くものとする。点P、Qが動き始めてからx秒後の4点A、B、P、Qを結んでできる図形の面積をy cm² とする。
(1) 0 ≤ x ≤ 12のとき、xとyの関係を表すグラフをかきなさい。
(2)四角形ABQPの面積が、台形ABCDの面積の4分の1になるのは点P、Qが動き始めてから何秒後ですか。
今日はこの応用問題を気合いで乗り切っていこう。
変域を考える
一次関数の動点では、
変域がいくつできるのか?
と見通しをつけるといいよ。
この問題では
点PがAから、点QがCから毎秒1cmの速さで動く
という条件があるね?
しかも、辺の端まできたら折り返して、12秒間動く、らしい。
12秒で四角形ABQPの面積 (y)はどのように変化するんだろう??
分け方のポイントは、
動点が頂点に到着するタイミングで分ける
だよ。
ADはBCより短いから最初に、点PがDに着く。
そして、点Pに遅れてちょっとして点QがBに辿り着く。
PとQは、頂点にたどり着くタイミングが微妙に異なるから、4つの変域が考えられそう。
- PがDに着くまで($0 ≤ x ≤ 4$)
- QがBに着くまで($4 ≤ x ≤ 6$)
- PがAに戻るまで($6 ≤ x ≤ 8$)
- QがCに戻るまで($8 ≤ x ≤ 12$)
それぞれの変域で、四角形ABCDの面積の変化をみればいいんだ。
PがDに着くまで($0 ≤ x ≤ 4$)
まずはPがAを出発してからDに着くまで。
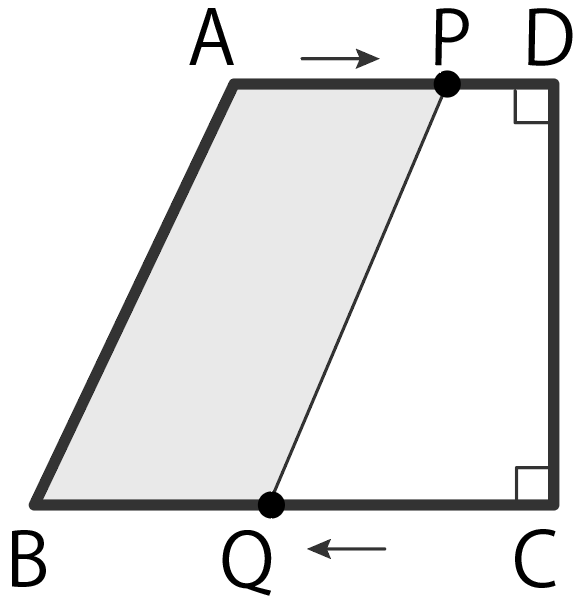
図をかくとわかるけど、四角形ABQPは台形になる。
で、面積を求めるために、
- 上辺 AP = x cm
- 下辺 BQ = ( 6 – x ) cm
- 高さ DC = 4 cm
という辺の長さが必要だね。
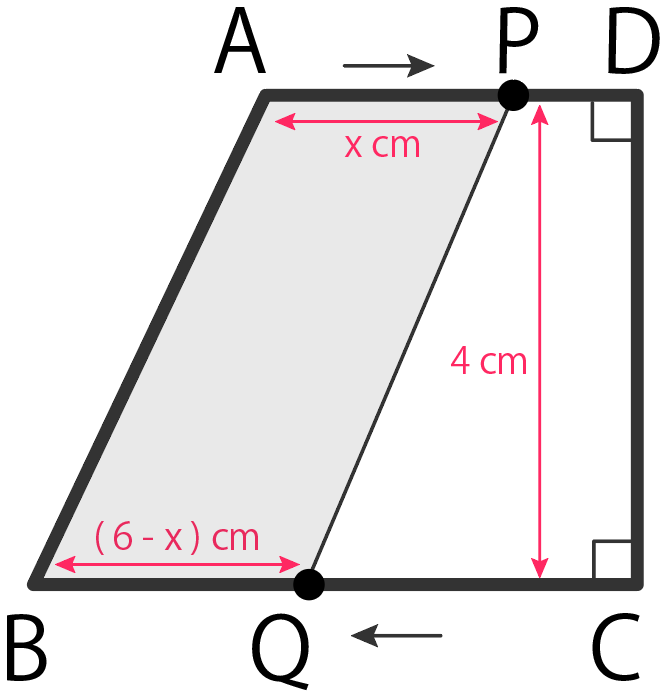
ポイントはBQの長さ。
QはCからスタートしてBに向かっているから
$$CQ= x cm$$
そして、そいつをBCの長さ 6 cm から引いたやつがCQの長さになるから、
$$BQ= BC – CQ$$
$$= 6 – x$$
になる。
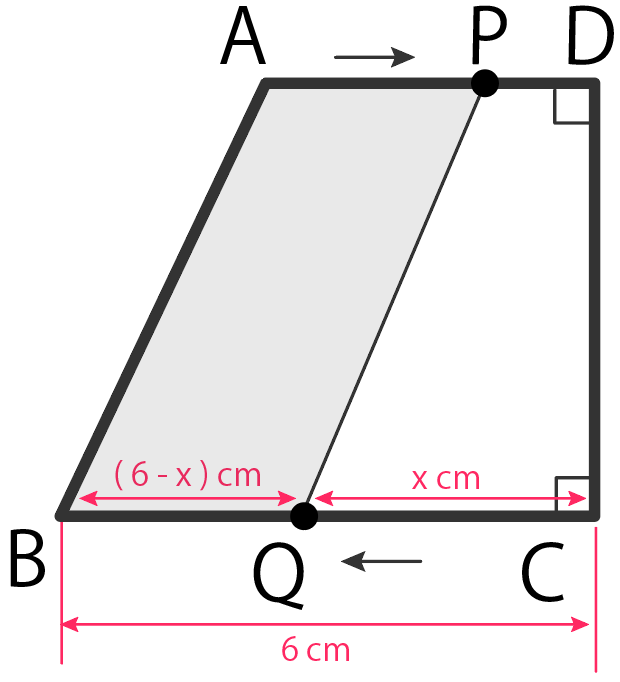
さて。ここで台形ABQPの面積yを計算しよう。
(上の辺+下の辺)×(高さ)÷2
だったから、
$$y = (AP+BQ)× DC ÷ 2$$
$$= (x +6 -x)× 4 ÷ 2$$
$$= 12$$
になる。
0〜4秒では、台形ABQPの面積はずーっと12ってこと。
QがBに着くまで($4 ≤ x ≤ 6$)
PがDに到着して、折り返しを始めたら、四角形ABQPの面積は変化するよ。
この場合、APの長さが変化してきていて、
$$8 – x$$
になってるはず。
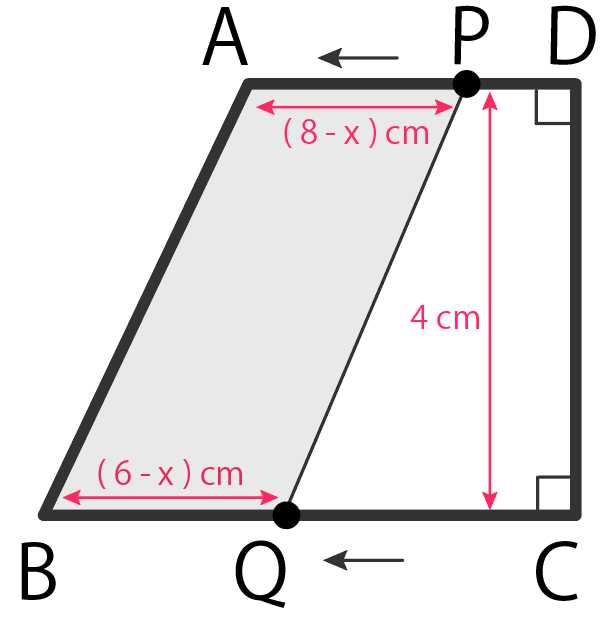
ADを2倍した長さから、Pが動いた距離「x」を引くとAPになるね。
ただ、相変わらず四角形ABQPは台形さ。
同じように台形の面積 y を計算すると、
$$y = (AP+BQ)× DC ÷ 2$$
$$= (8-x +6 -x)× 4 ÷ 2$$
$$= -4x + 28$$
になる。
この式から分かるのは、
このフェーズ($0 ≤ x ≤ 4$)では時が経つにつれて面積が小さくなるってこと。
PがAに戻るまで($6 ≤ x ≤ 8$)
お次はPがDに到着して、PがAに戻るまでの時間。
6〜8 秒までだね。
ここでのポイントは、BQの長さが変化していること。
QはBに到着して、折り返しているから、
BQ=
Qが進んだ距離 – BCの長さ
= x – 6
になる。
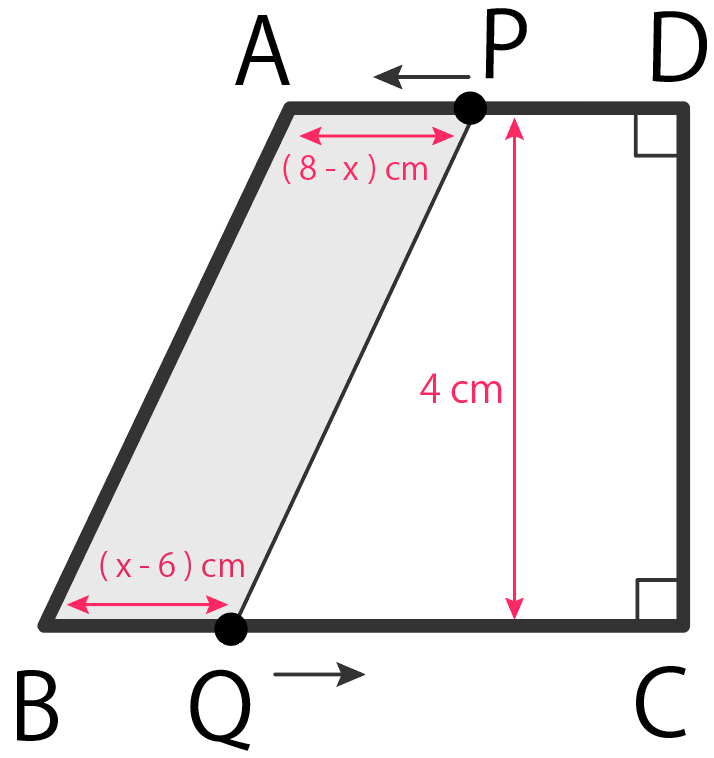
すると、四角形ABQP(というか台形)の面積yを計算すると、
$$y = (AP+BQ)× DC ÷ 2$$
$$= (8-x +x – 6)× 4 ÷ 2$$
$$= 4$$
になるね。
あら不思議。
またまた面積yが一定になっちゃった。
QがCに戻るまで($8 ≤ x ≤ 12$)
最後はQがCに戻るまで。
このタイミングは、Pが2回目にDに到着するタイミングでもあるとも言えるね。
変域で表すと
$$8 ≤ x ≤ 12$$
になる。
この時ポイントは、APの長さが変化していること。
PはAに到着して、折り返してDを目指しているはず。
だから、
APの長さ
=Pが進んだ距離 – ADの2倍の距離
= x – 8
になる。
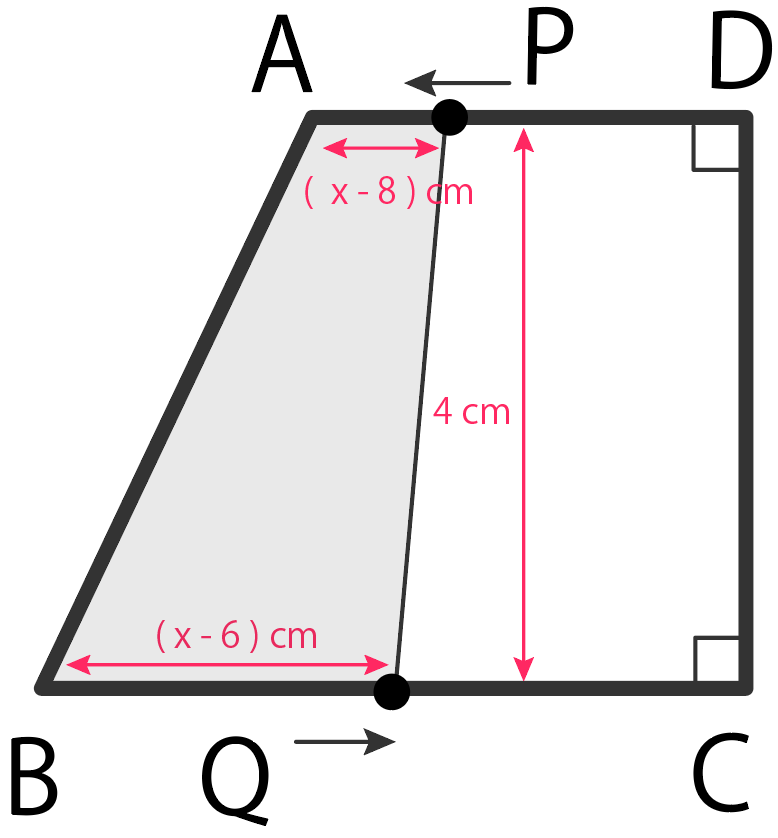
四角形ABQP(というか台形)の面積yを計算すると、
$$y= (AP+BQ)× DC ÷ 2$$
$$= (x – 8 +x – 6)× 4 ÷ 2$$
$$= 4x – 28$$
になる。
ふう、これで全部の変域における関数式が出せたぜ。
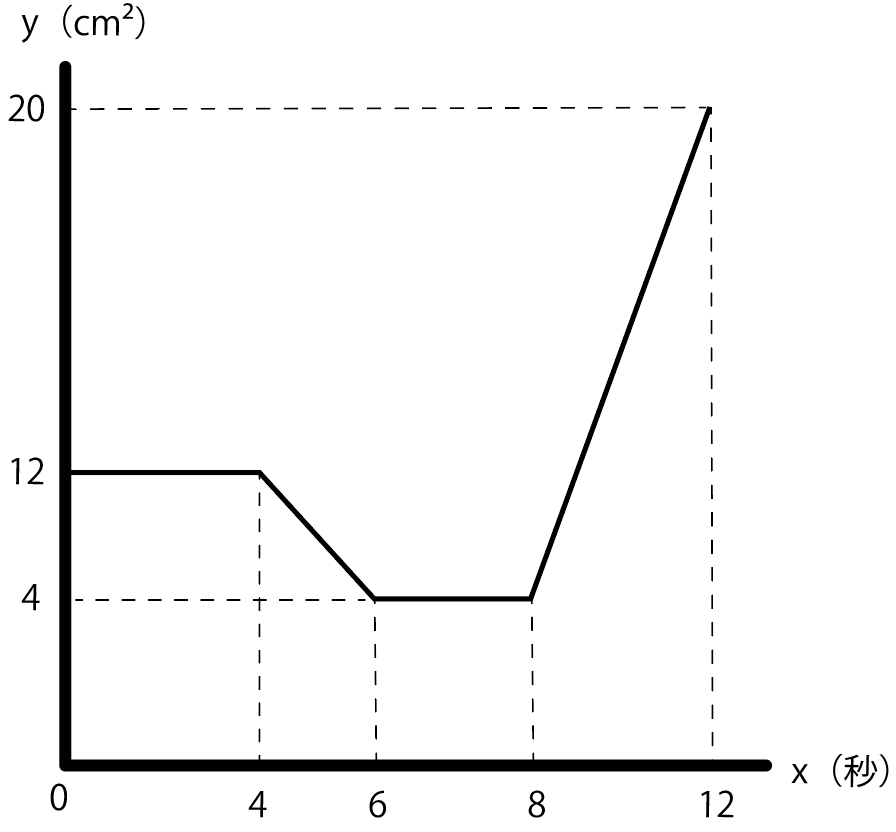
それぞれの式をグラフにするとこんな感じ。
四角形ABQPが台形ABCDの4分の1になるのはいつ?
あと1つやることがある。
それは、例題の(2)の
四角形ABQPの面積が、台形ABCDの面積の4分の1になるのはいつ?
に答えること。
つまり、これ、
yが特定の値になる時のxを求めよ
という問題だ。
まずは「台形ABCDの面積の4分の1」がいくつか探っていこう。
台形ABCDは上辺が4、下辺が6、高さが4の台形だから、
$$(4 + 6 )× 4 ÷ 2$$
$$= 20 cm²$$
という面積になる。この4分の1は「$5 cm²$」だ。
ここで、さっき適当にかいたグラフに注目。
yが「5 」になっている箇所を探してみると、2つヒットだ。
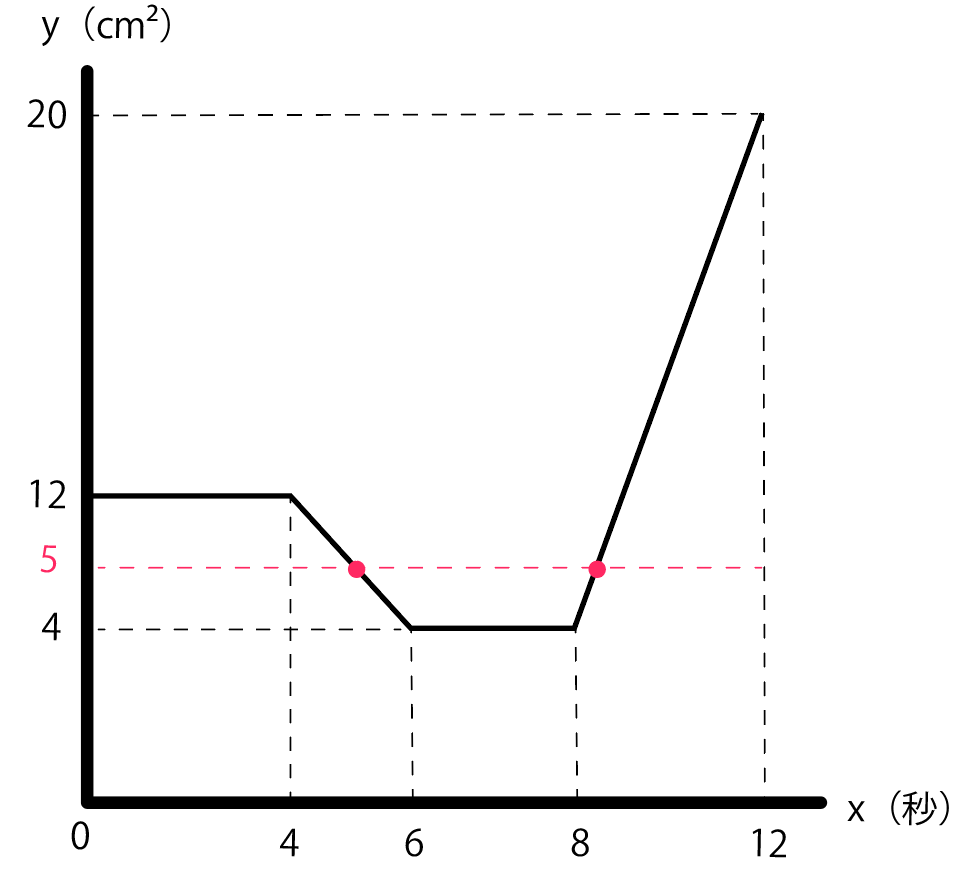
- QがBに着くまで($4 ≤ x ≤ 6$)
- QがCに戻るまで($8 ≤ x ≤ 12$)
という2つの変域でyが5になる瞬間があるじゃないか。
ということで、これら2つの変域の関数にそれぞれ$y=5$を代入して、その時のxを求めればいいことになる。
まず、QがBに着くまで($4 ≤ x ≤ 6$)の場合。
$$y = -4x + 28$$
に $y = 5$を代入すると、
$$5 = -4x + 28$$
$$x= \frac{23}{4}$$
になるね。
あと1つは、QがCに戻るまで($8 ≤ x ≤ 12$)の場合。
$$y = 4x -28$$
に$y = 5$を代入しよう。
すると、
$$5 = 4x -28$$
$$x = \frac{33}{4}$$
になる。
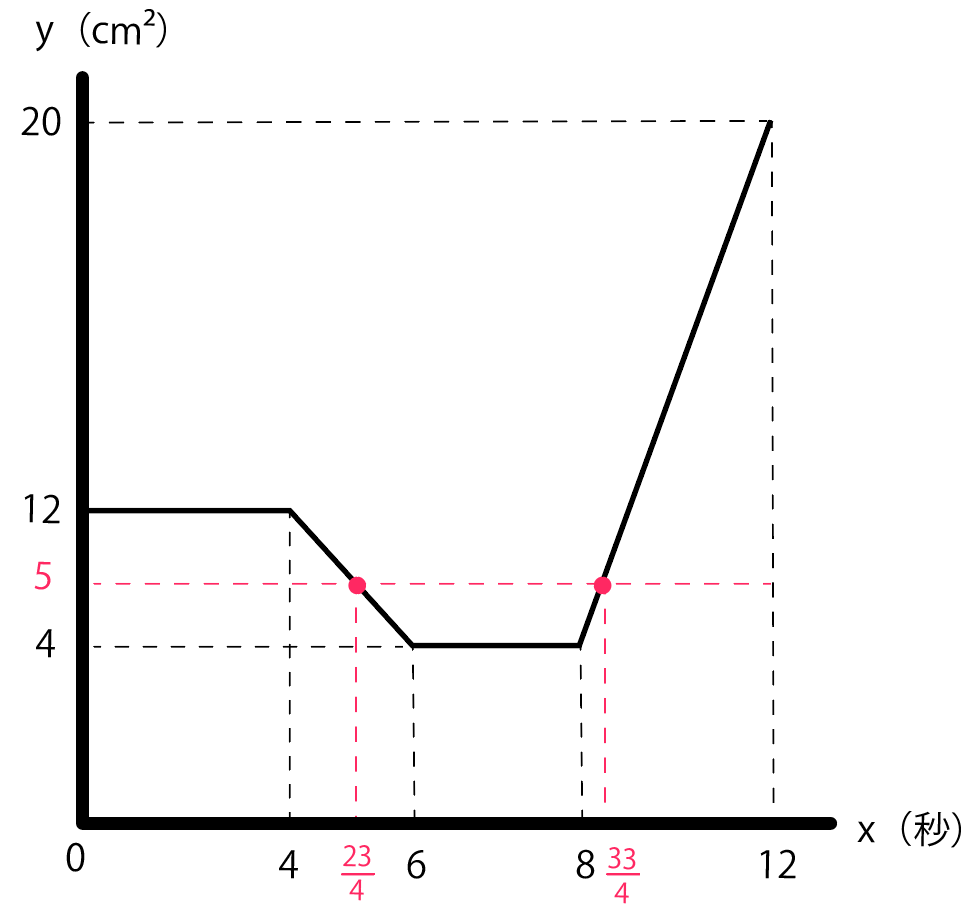
ってことで、四角形ABQPの面積yが$5 cm²$になる時間は、
- $\frac{23}{4}$秒
- $ \frac{33}{4}$秒
の2つだ。
いやーほんとおつかれさま。
動点が2つあるとこんなに厄介だとは思わんかったな。
応用問題では出現することがあるから対策しておこう。
そんじゃねー
Ken



