【中2数学】文字式の利用の問題の解き方がわかる3ステップ
文字式の利用の解き方がさっぱりわからん!?
こんにちは!この記事をかいているKenだよ。うたたねが得意だね。
中2数学の「文字式の利用」はけっこうむずい。
ここでは、
文字式を利用して「すごいこと」をしなきゃいけないんだ。
ただ計算するだけじゃ許してくれない。
まったく、中2数学もきついね。

今日は、中2数学の山場ともいえる、
文字式の利用の問題の解き方
を3ステップで解説していくよ。
つまずいたときに参考にしてみてね。
文字式の利用の問題の解き方がわかる3ステップ
文字式の利用の解き方はたったの3ステップさ。
例題をときながらみていこう!
2つの整数が、偶数と奇数のとき、その和は奇数になります。そのわけを説明しなさい。

Step1. 数字を文字式であらわすっ!
問題文の「数字」を「文字」であらわしてみよう!
イメージでいうと、
「数字」っていう野菜を、
「文字」っていう包丁で切って「文字式」っていうカレーをつくるって感じw

えっ。ちょっと想像できないだって??w
それじゃあ例題をみていこう。

例題では「偶数」と「奇数」っていう2種類の数字がでてきたね。
こいつらを文字で表現してやればいいのさ。
m、nを整数とすると、
- 偶数 = 2m
- 奇数 = 2n +1
と文字式ができるね。
だって、偶数は2で割り切れる数だからね。
ってことは、ある整数を2倍した数ってことになるでしょ??
また、奇数は「偶数に1を足した数」だから整数を2倍して1を足せばいいんだ。
これで偶数と奇数という「数字」を、
m・nという「文字」であらわせたね。
Step2. 言われたことを実際にやってみる。
文字式を使って指示されたことをやってみよう。
文字式の利用では、必ず、
数字の文字式をつかって何かしてみて??
っていうメッセージが込められているんだ。
よーく問題文を読み返してみよう!

問題文を読み直してみると、
「その和は奇数になります」
っていう文にメッセージが隠されていない??
そう。
そうなんだよ。
この文章では、
「偶数」と「奇数」を足してみて??
っていうダイイングメッセージが込められているんだ。
コナンでもきっと読み取ってくるだろう。
つまり、この問題では、
「偶数」と「奇数」をたして「奇数」になるよー
ってことをいってあげればいいんだ。
だから、まずはその2つをたしてやるのさ。
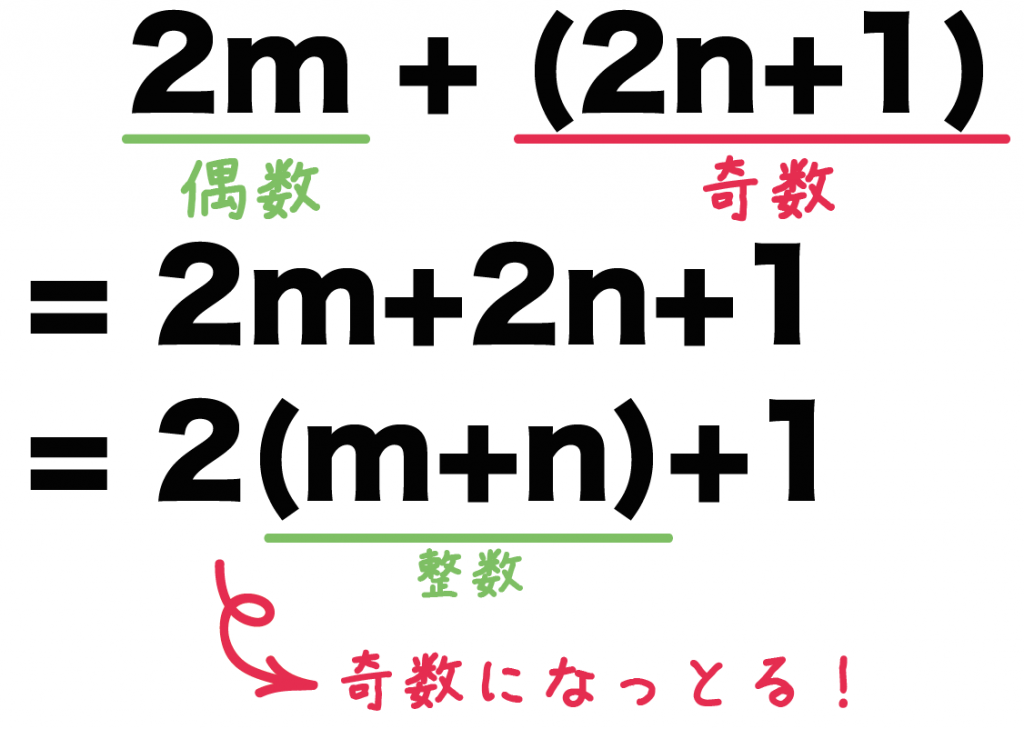
実際に「偶数(2m)」と「奇数(2n+1)」をたしてやると、
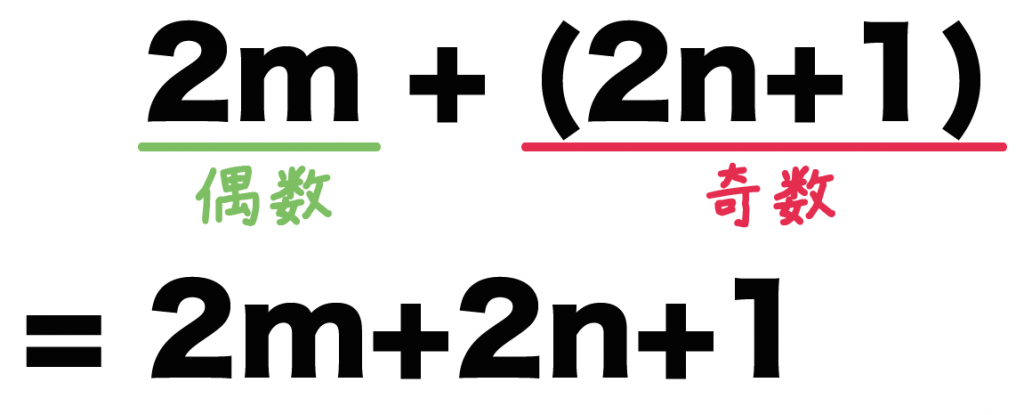
2m + (2n+1)
= 2m+2n+1
になるね!
Step3. ゴールに力技で着地する
あとは問題文の「ゴール」に力技で着地するだけさ。
問題文をよーく読んで、
何をすればゲームクリアなのか??
ということを見極めよう!
たいてい、メッセージ後に「ゴール」が潜んでいることが多いよ。
例題の文章をもう1度読んでみよう。
すると、
「その和は奇数になります」
という文から、
「偶数」と「奇数」の和が「奇数」になること
がゴールだと読み取れるはずだ。

つまり、
偶数と奇数をたしたら奇数になる!
って言ってやれば問題でマルがもらえるってわけさ。
奇数ってことは、
整数×2+1
になってればいいよね??
2m + 2n +1
という文字式のmとnを係数2でかこってあげると、
2(m+n) +1
になるね。(m+n)は「整数+整数」で「整数」になるから、
2(m+n) +1 は「奇数」
ってことがいえるんだ。
これで、問題のゴールの、
「偶数と奇数の和は奇数になる」
ってことがいえたわけ!
おめでとう。
これで文字式の利用の解き方もゲットだね!
まとめ:文字式の利用の解き方は「ゴールの見極め」がカギ
文字式の利用の解き方は、
- 数字を文字式であらわす
- 言われたことをする
- ゴールに着地するためにへりくつを言う
の3ステップだったね。
この中でもっとも重要なのは、
問題文からゴールをみつける
ということ。
これさえできれば、どんな文字式の利用の問題でも大丈夫!
問題に慣れてテストをむかえてみてね。
そんじゃねー
Ken