【相似の利用】縮図問題の解き方がわかる3ステップ
相似の利用で縮図がでてきた!!
こんにちは!この記事をかいてるKenだよ。甘さを極めたね。
相似な図形で最後にでてくるのは、
相似の利用
っていうモンスターだ。
これはおもに、
相似を現実世界でもつかってみよう
というもの。
むちゃくちゃ実践的だから、
相似の証明より100倍ぐらいおもろいよ。
その相似の利用でよくでてくるのが、
縮図の問題
なんだ。
今日はこの問題を解説していくよ。
よかったら参考にしてみてね。
相似の利用の縮図問題の解き方3ステップ
さっそく問題をといてみよう。
つぎの例題をみてみて。
映画「ザ・ウォーク」の主人公にまつわる問題なんだ。
練習問題
とある、むかし。
綱渡りで飯をくってる男が、いた。
野心が強すぎた彼は、ニューヨークの高層ビルに縄をかけて、
綱渡りしたいと思ってたのだ。
そこで、ビルとビルの間の距離を測らなきゃいけない。
縄をはらなきゃいけないからね。
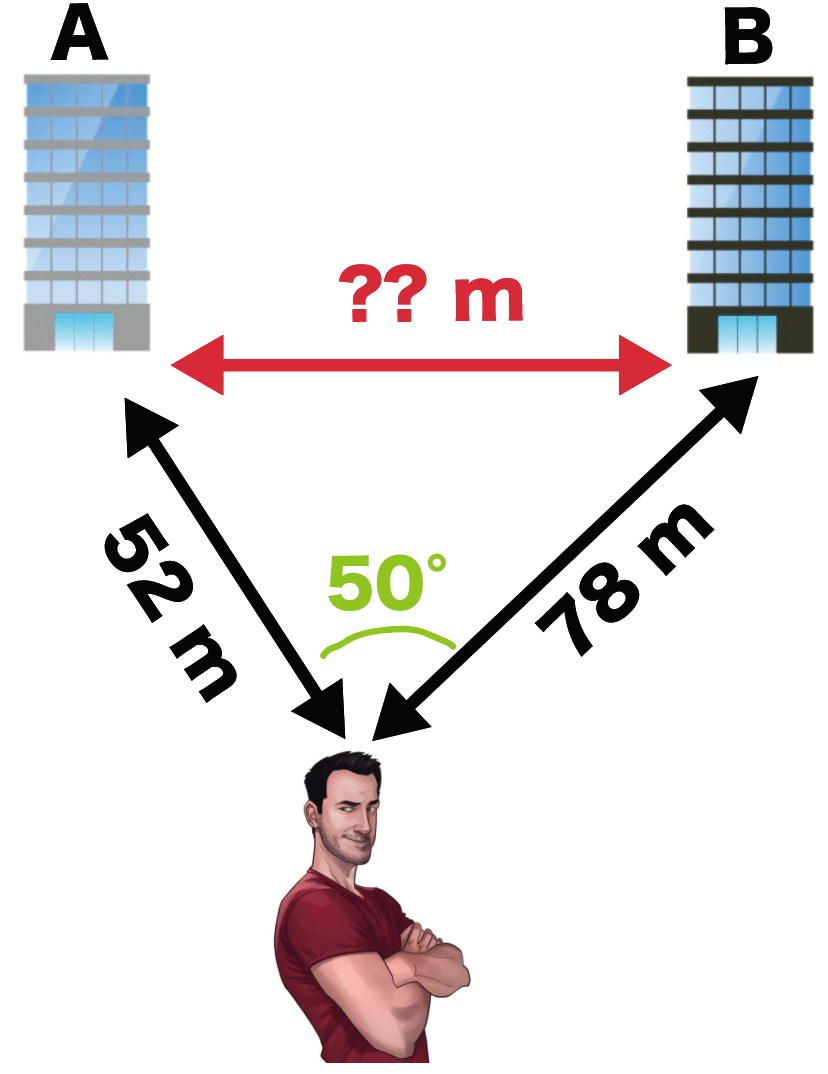
ただ、いま彼がわかっているのは、
自分の現在地から2つのビルまでの距離
と、
角度
だけ。
- ビルAまでの距離は52m
- ビルBまでの距離は78m
- 2つのビルの角度50°
だ。
彼は縮図をつかって、
ビルの距離をはかることを思いついたのだった。
彼よりもさきに縮図でビル間の距離を計測しなさい。
ただし、400分の1の縮図をつかうこと。
この手の問題は3ステップでとけちゃうよ。
- 縮図をかく
- 縮図の距離をはかる
- 何倍かする
Step1. 縮図をかく
まずは縮図をかこう。
現実世界よりも小さい図をかけってことだね。
練習問題では、400分の1の縮図をつかえっていわれているから、
400分の1にした図をかいてみようか。
まずは、ビルまでの距離の、
- 52 m
- 78 m
をcmの単位になおしてみよう。
1m = 100cmだから、
- 52 m = 5200 cm
- 78 m = 7800 cm
だよね??
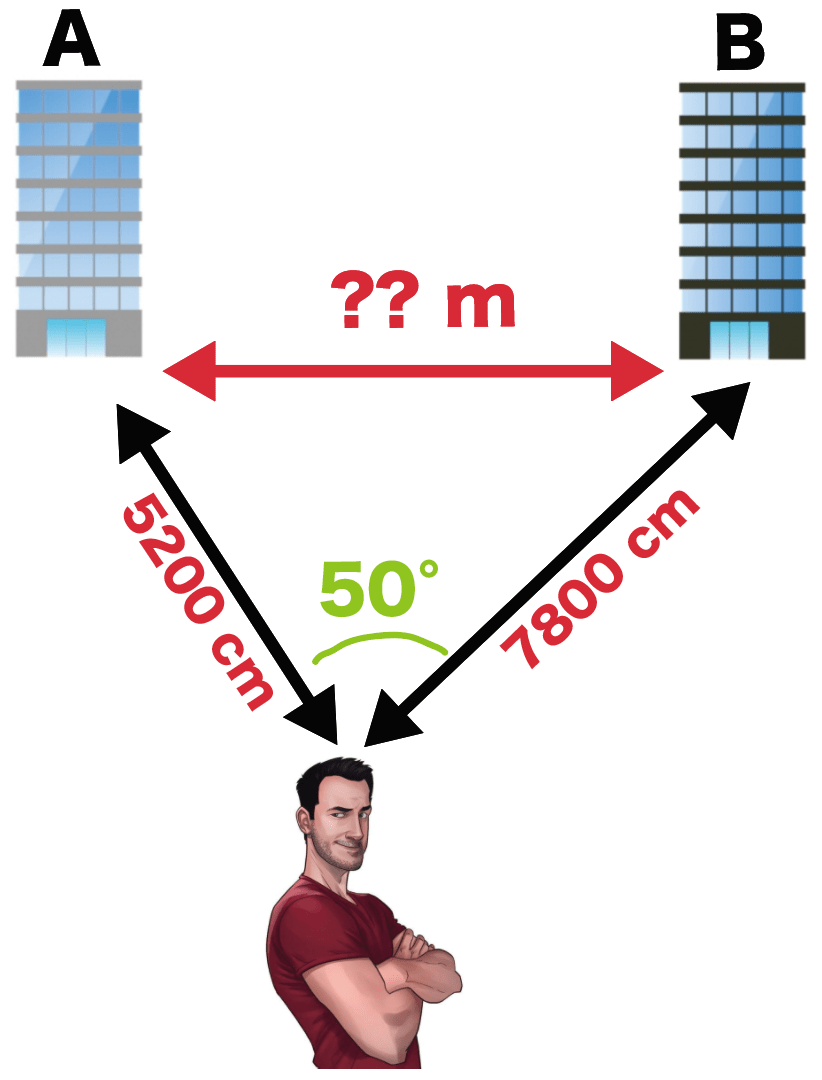
こいつを400分の1に小さくすると、
- 5200 cm ⇒ 13 cm
- 7800 cm ⇒ 19.5 cm
になる。
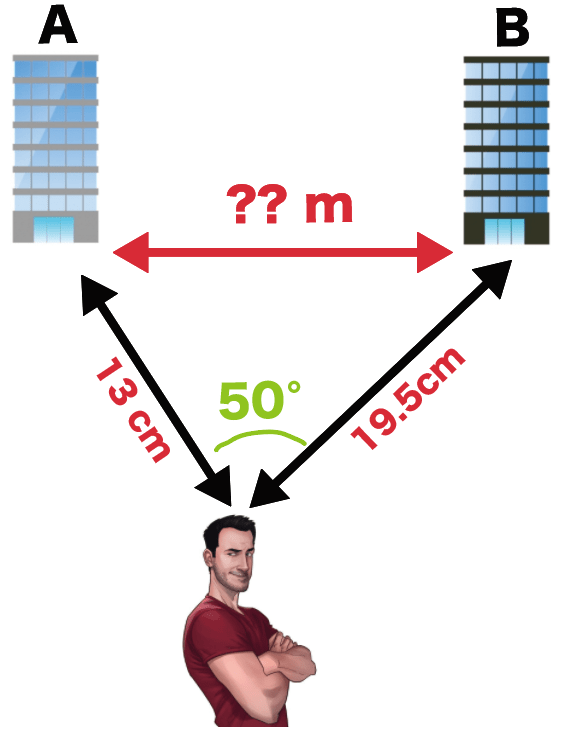
実際に縮図を作図してみよう。
まず男がいる地点を縮図上に点をうつ。

つぎに、適当な方向に13cmの線を、ひく。
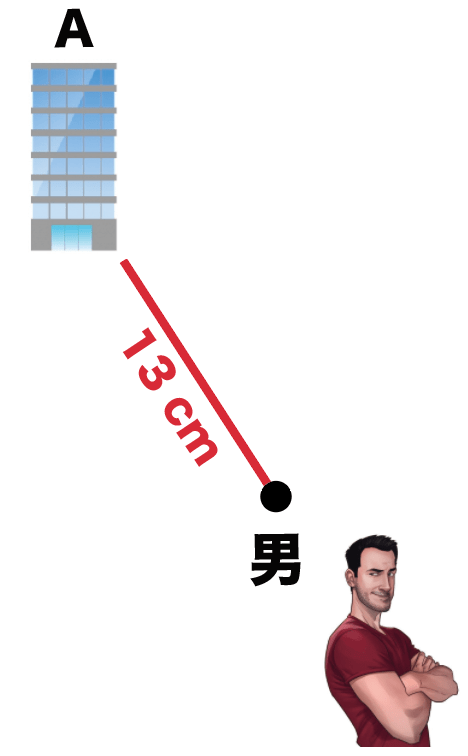
これは男からビルAまでの縮図上の距離だね。
つぎは分度器の出番。
分度器で男の点から50°をはかって、
適当に直線をひいてみよう。

そしたら、今度は男からビルBまでの縮図上の距離の、
19.5cm
をはかってあげる。
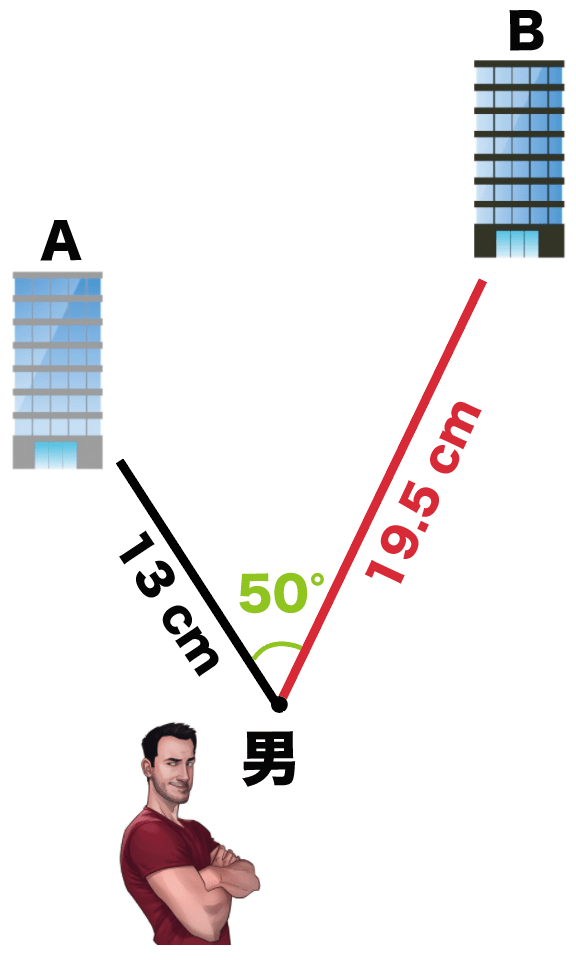
あとは、ビルとビルの間を線でむすぶだけ。
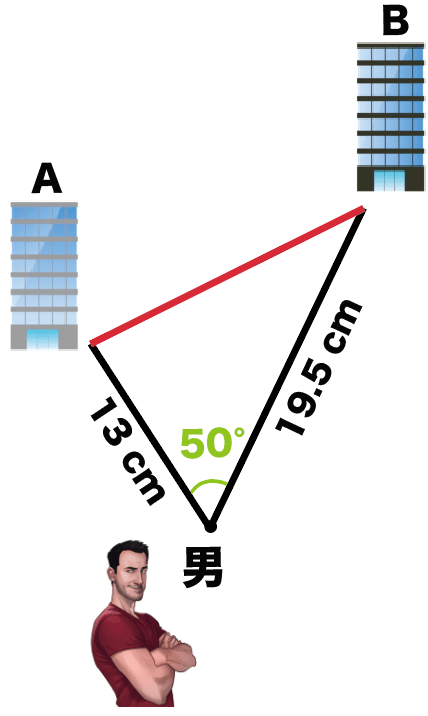
これで縮図の完成だ!
Step2. 距離をはかる
つぎは、縮図の長さをはかろう。
問題で求めたい長さ
をはかればいいんだ。
練習問題では、
ビルAとビルBの距離
だったよね??
縮図上で、2つのビルの距離をはかってみると、
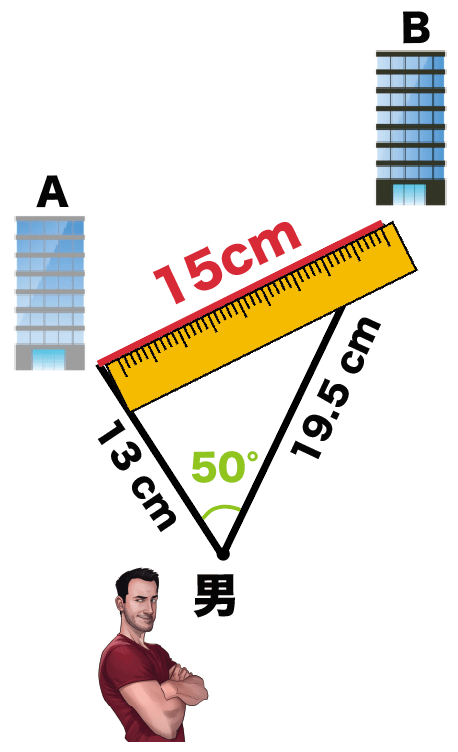
うわっ!
15 cm
になってるじゃん!!
Step3. 縮図をもとにもどす
最後はリアルな長さにもどしてあげよう。
つまり、
縮図の倍率をかければいいのさ。
今回の練習問題では、
400分の1の縮図だったね??
だから、縮図を400倍してやると、リアルな大きさになるわけよ。
ビルとビルの間は縮図上は15 cm。
こいつを400倍すると、
リアルな世界のビルとビルの距離になるんだ。
ってことで、リアルな世界のビル間の距離は、
15 × 400
= 6000 cm
= 60m
ってわけだね。
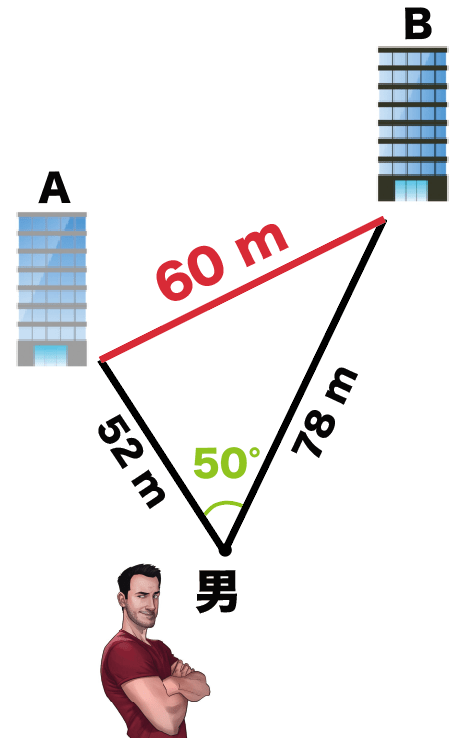
縮図からビルとビルの距離を求められたね。
あとは、60m以上の縄を買って渡るだけだ。

ふぁいつ!
まとめ:相似の利用の縮図は作図にかかってる
相似の利用の縮図はどうだったかな??
ぶっちゃけ、相似の利用の縮図問題は、
作図の正確さ
が重要になるんだ。
分度器と定規で精密な作図をしてみてね。
それじゃあ!
Ken


