【中学数学】3年間つかえる証明問題の書き方
数学の証明問題の書き方がわからん!?
こんにちは!この記事をかいているKenだよ。図書館、最高。
数学の証明はむずいよね??
雰囲気がめんどいのはもちろんだけど、
それ以上に、
証明の書き方がわからない!
からだと思うんだ。
だって、
先生ごとに書き方ちがうからね。
誰を信じたらいいのかわからなくなっちゃう。

そこで今日は、
【中学数学】3年間つかえる証明問題の書き方
って記事をかいてみたよ。
困ったときに参考にしてみて。
中学数学でつかえる証明問題の書き方
証明の書き方でおぼえてほしいのは、
型だよ。
ちまたではテンプレートともよばれてる。
そうだなあ、
クッキーを思い浮かべてほしい。
だいたい同じような形のクッキーが焼けるのって、
型があるからなんだ。
だから、
数学の証明でも「型」を使いこなせれば、
それっぽい証明が何個でもつくれることになるね。
数学の証明の型(書き方)って??
書き方の「型」はつぎのものだよ。
先生ごとによって書き方ちがうけど、
ぶっちゃけどれもこんな感じだ↓↓
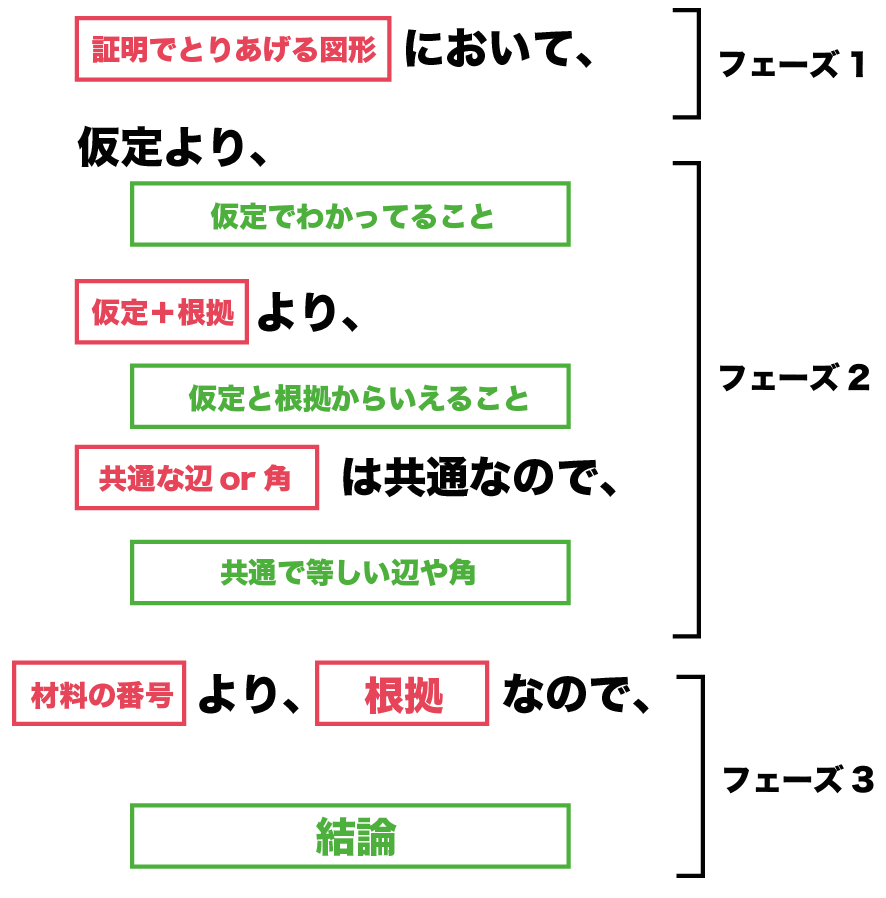
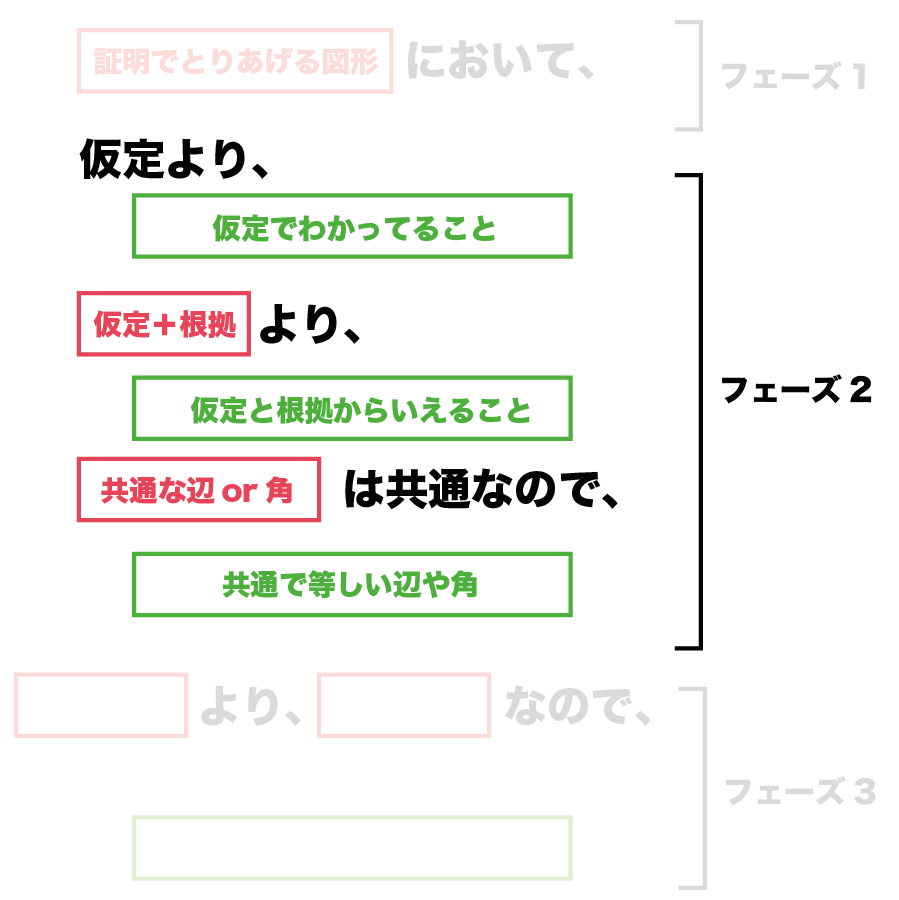
(証明でとりあげる図形)において
仮定より、
(仮定よりわかっていること)
仮定+根拠より、
(仮定と根拠からいえること)
(共通な辺or 角)は共通なので、
(共通で等しい辺や角)
(材料の番号)より、(根拠)なので、
結論
じつはこの型、
- 戦うフィールドを選択する
- 結論をみちびくための材料をとりあげる
- 結論をいう
っていう、3つのフェーズにわかれている。
この「型」で例題をといてみよう!
例題
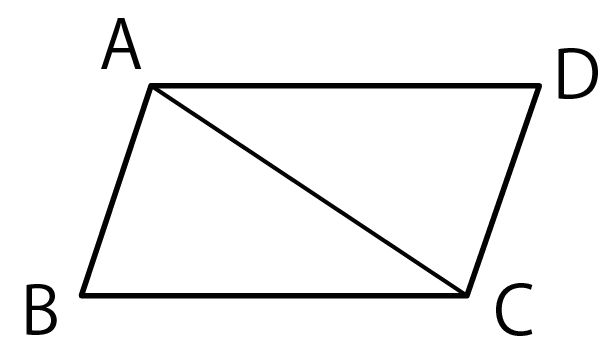
AB = DC、AB // DCの△ABCと△CDAがあったとします。
このとき、△ABC≡△CDA
を証明しなさい。
フェーズ1. 証明でとりあげる図形を宣言する!
書き方のいちばん最初は、
どの図形を証明でとりあげるのか??
を宣言することなんだ。
〜において
ってかいて、
「〜」には「証明でとりあげる図形」をかいてあげよう。
例題では、
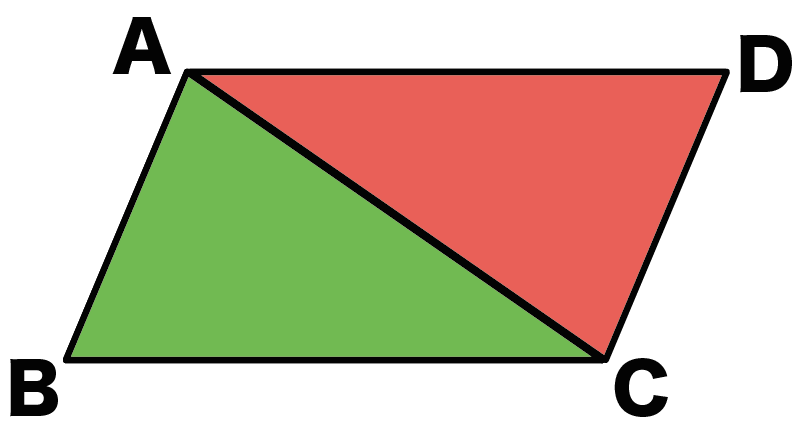
△ABCと△CDAの合同を証明していくよ。
ってことは、この証明ではおもに、
△ABCと△CDA
の話をしていくことになるんだ。
だから、証明のいちばん最初で、
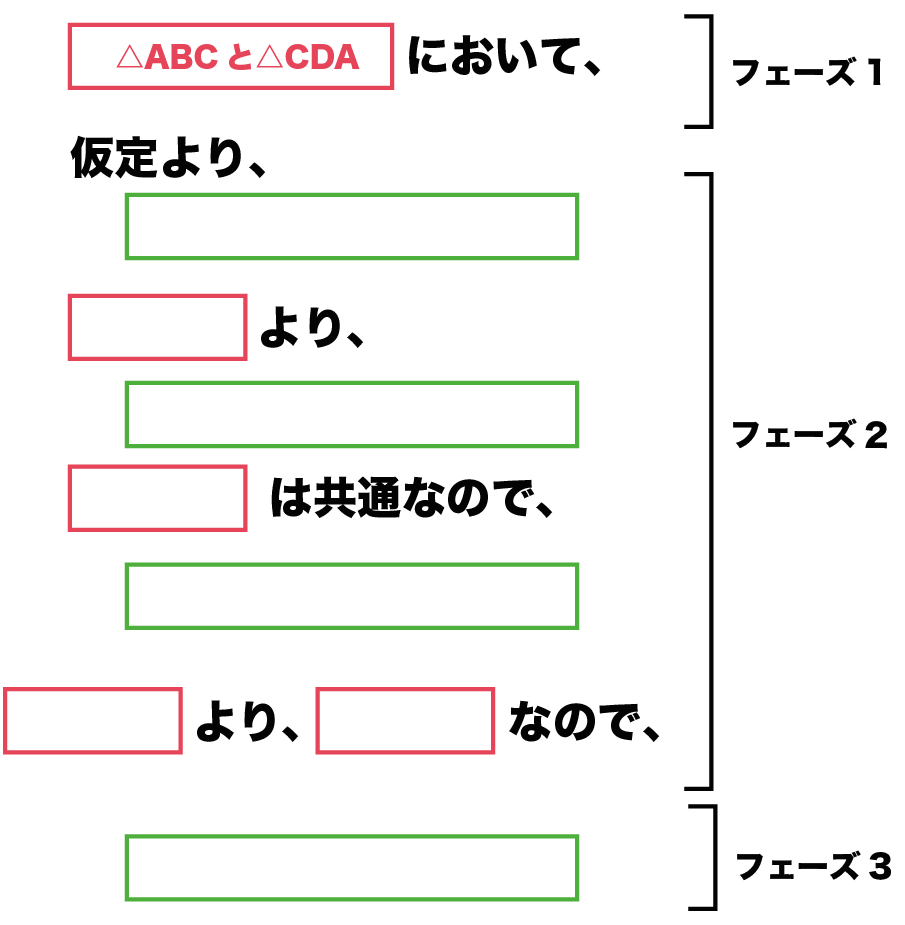
△ABCと△CDAにおいて、
って証明でとりあげる図形を宣言してみて!
このフェーズはぶっちゃけ、
あってもなくても構わない。
だけどこいつをかいてやることで、
- 頂点の対応順のミスをなくせる
っていうメリットがあるんだ。
ぜひ、証明のいっちゃん最初に
「証明でとりあつかう図形」を宣言してみてくれ!
フェーズ2. 結論をみちびくための材料を羅列する
結論に必要な材料をならべるフェーズだ。
- 問題文でわかっていること
- それらからわかること
をどんどんかいていこう!
結論の材料の並べ方はつぎの3パターンがあるよ。
- 「仮定」より、+「仮定をそのまま」
- 「仮定+根拠」となることがらより、「仮定とその根拠からわかること」
- 「〜は共通」より、「共通となっている等しい辺や角」
このパターンをぜんぶ使わなくてもOK。
1つでも2つでも、ぜーんぶつかってもいいよ。
その証明に必要なものをチョイスしてみてね。
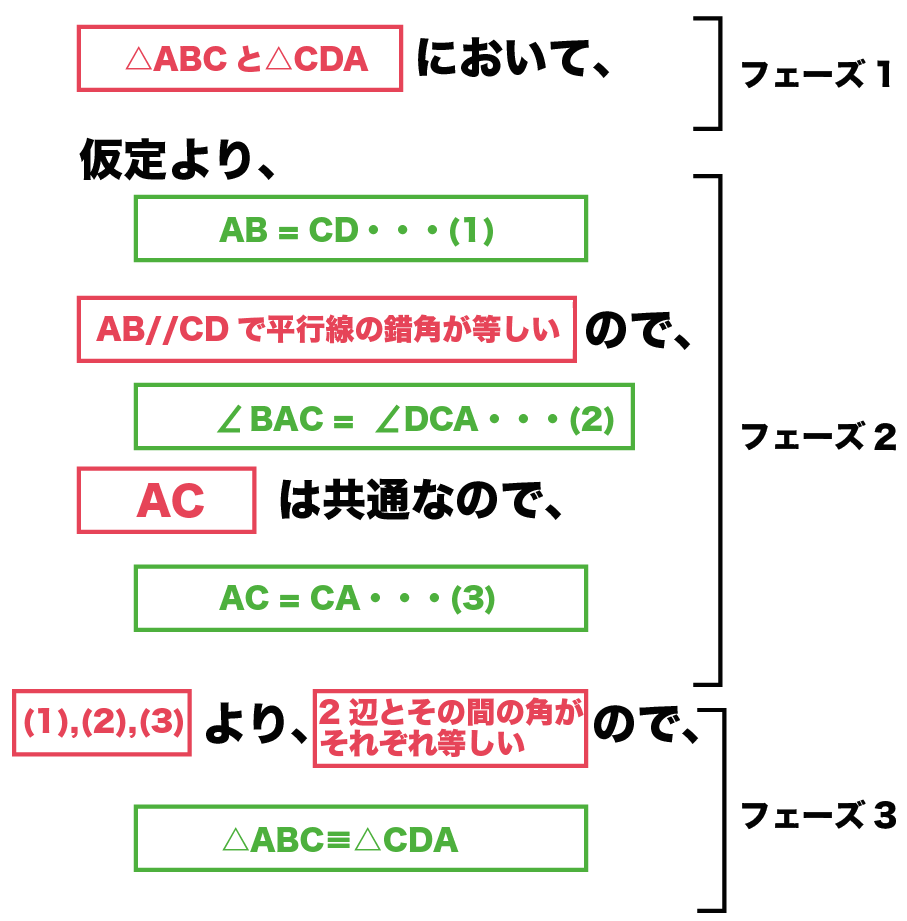
例題ではこんな感じになる↓↓
それぞれに番号ふるのを忘れずに!
フェーズ3. 結論をいったる!
最後はいよいよ結論。
フェーズ2で生み出した材料から、
結論(証明のゴール)
をみちびいてやろう。
書き方としては、
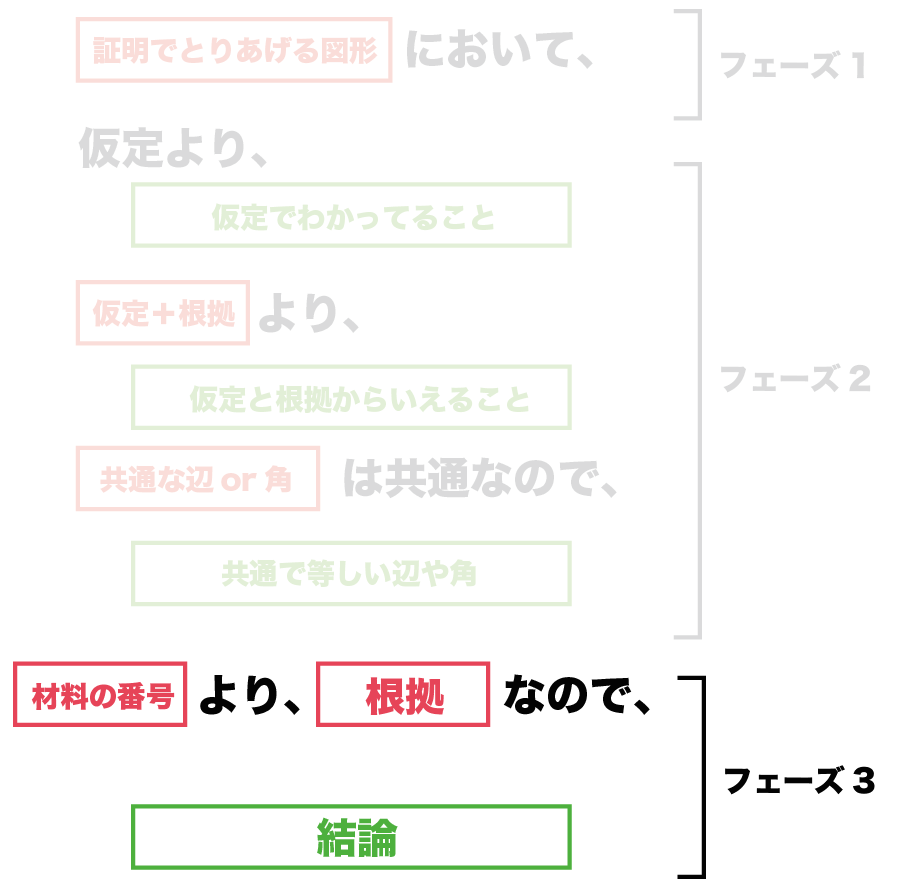
(材料の番号)より、(根拠のあることがら)なので、
(結論)である。
がのぞましいね。
例題でいうと、こうなる↓↓
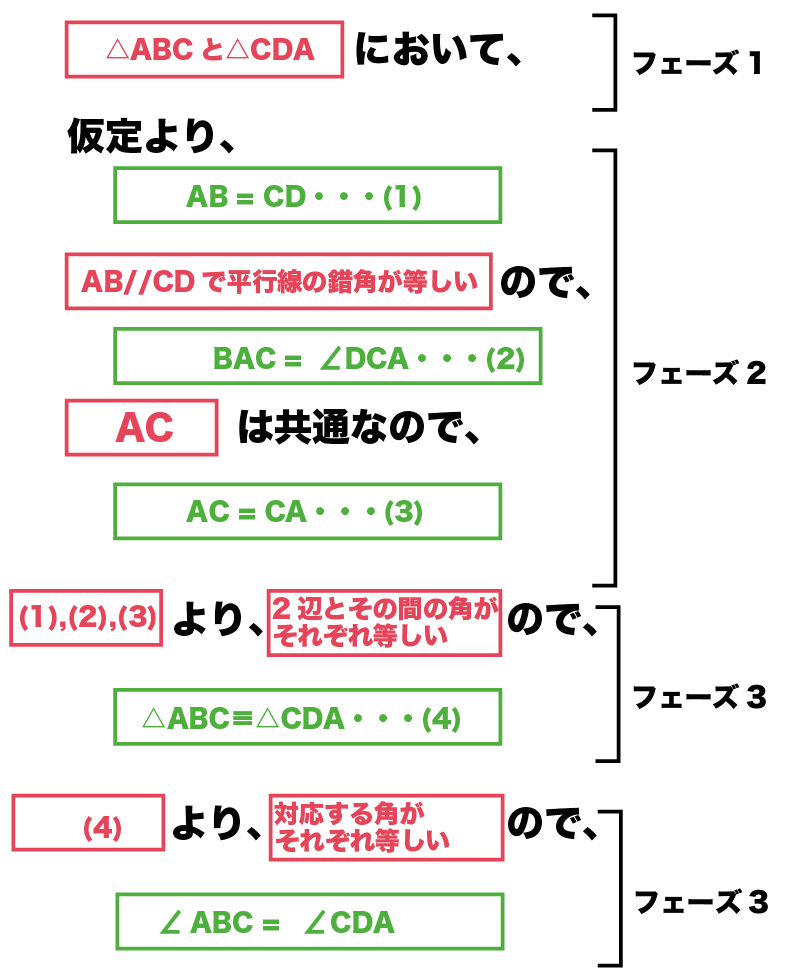
もし、結論が「角ABC = 角CDA」だった場合は、
もう一回フェーズ3をくり返してみてね。
こんな感じで、問題によって、
フェーズ2や3が数回くり返すこと
もあるよ!
必ずしもこの型がピタリとはまるわけじゃないから、
気をつけてね。
まとめ:数学の証明は書き方おぼえればどうにかなる!
数学の証明はぶっちゃけむずい。
解き方もようわからん。
だけど、
書き方の「型」をおぼえてしまえば大丈夫。
それ通りにかいていくだけでいいからね!
問題をときまくって書き方になれていこう!
そんじゃねー
Ken