【中2数学】証明とはいったいなにもの??
数学の証明とはいったいなにものなん?
こんにちは!この記事をかいているKenだよ。トイレットペーパーに助けられたね。
中学2年生になると、
数学の証明
がはじまる。
いままでの数学では、
図形の面積をだしたり、
xにyを代入したりすればよかったね。
だがしかし、証明はそーはいかない。
ぜんぜんタイプが違うんだ。
むずいというか、うざい。
そんなタイプの単元だ。
今日はやっかいな証明を攻略していくために、
証明とはなにか??
ということを解説していくよ。
証明とは「あること」が事実だと明らかにすること?
Wikipediaによると「証明」とは、
ある事柄が真理もしくは事実であることを明らかにすること
ってかいてあるね。
んでもこれじゃあ、よくわからない。
「数学の証明」って何を明らかにするんだろう??
って疑問に思うはずだ。
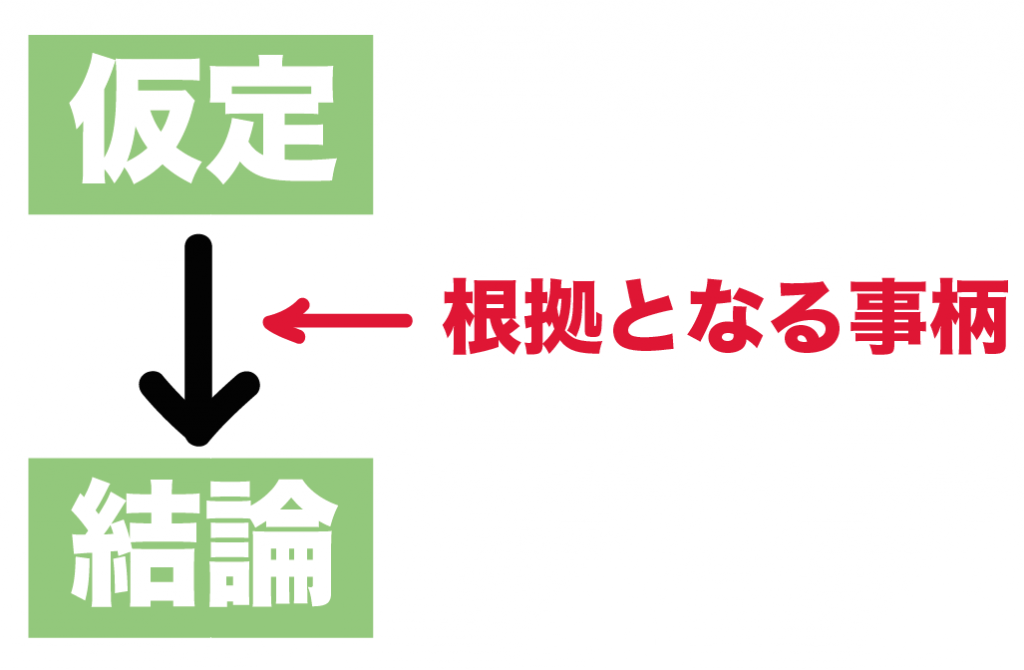
数学の証明とは簡単にいうと、
ある仮定(問題文であたえられている条件)が成り立つとしたときに
結論(証明のゴール)が正しいと明らかにすること
なんだ。
「仮定」から「結論」を明らかにするために、
いままでならってきた
「根拠となることがら」をつかっていくよ。
「根拠となることがら」ってたとえば、
三角形の合同条件とか、
対頂角は等しい
とかだね。
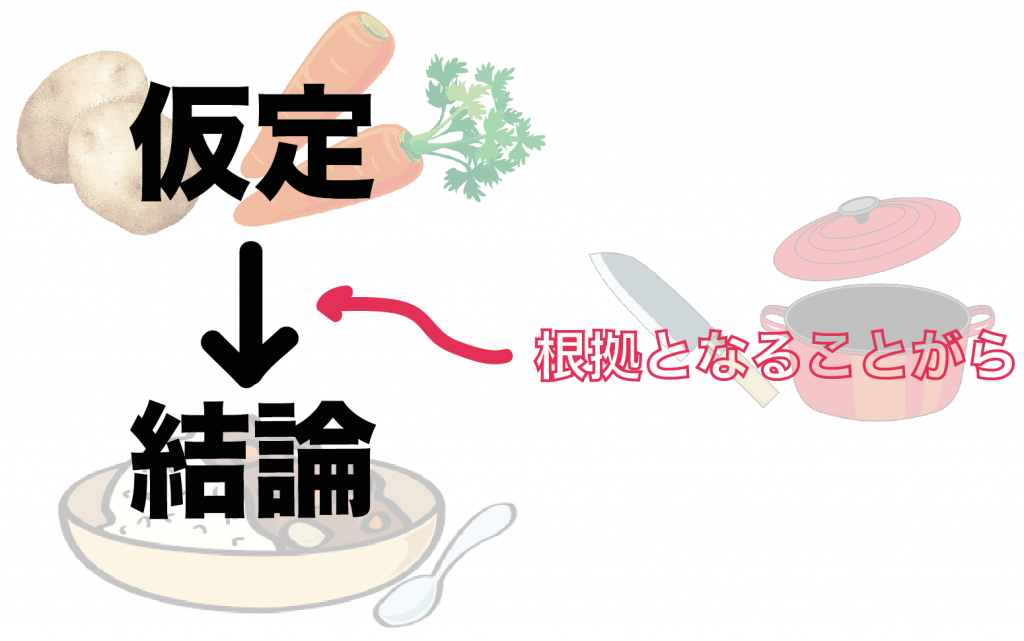
イメージでいうと証明は「カレー作り」に似ている。
仮定っていう「具材」を、
根拠のあることがらっていう「包丁」とか「鍋」で調理して、
結論っていう「おいしいカレー」をつくる
って感じ。
だから証明の問題では、
いかに多くのの「根拠となる事柄」(包丁や鍋)をつかって、
仮定(具材、ルー)から結論(カレー)をみちびくか??
がポイントなのさ。
つまり、
「根拠となることがら」をたくさん暗記すると有利ってことになるね。
中学数学の証明の例をみてみよう!
証明の例を紹介するよ。
つぎの例題をみてみて。
例題
つぎの三角形ABCと三角形DEFが合同であることを証明してください。

仮定と結論の整理
まず仮定(問題文であたえられている条件)
と、
結論(証明のゴール)
を整理してみよう。
この問題の仮定は、
- BC = EF = 6 cm
- 角B = 角 E = 60°
- 角C = 角F = 70°
だね。だって、問題文がそう言ってるからさ。
んで、
結論は、
- △ABC ≡ △DEF
だ。
この2つの三角形が合同だってことをいえばゴールってわけ。
証明をかいてみよう!
証明は基本的に、
- 仮定(問題文であたえられている条件)
- 根拠となることがら
- 結論(証明のゴール)
の順番でかいていけばいいよ。
実際に例題の証明をかいてみるとこうなる ↓↓
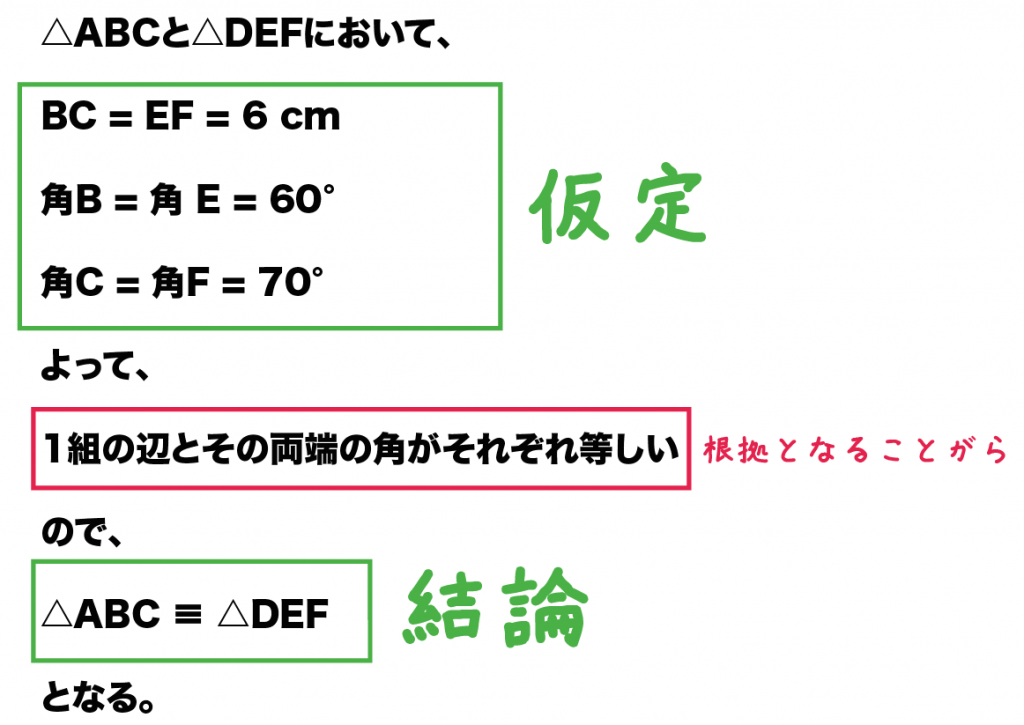
△ABCと△DEFにおいて、
BC = EF = 6 cm
角B = 角 E = 60°
角C = 角F = 70°
よって、
1組の辺とその両端の角がそれぞれ等しい
ので、
△ABC ≡ △DEF
となる。
っていう感じ。
- 仮定
- 根拠となることがら
- 結論
っていう順番になっていることを確認してね^-^
まとめ:証明とはカレー作りである。
証明ってはじめてきくと、むちゃくちゃむずそう。
でも大丈夫。
証明なんてただの「カレー作り」さ。
「仮定」っていう具材を、
「根拠となる事柄」をつかって調理して
「結論」っていうカレーをつくってあげよう!
そんじゃねー
Ken