一次関数の傾きの求め方がわからない？？
こんにちは！この記事をかいているKenだよ。メイド喫茶、たまにはいいね。
家が傾いてる
とか
うちの旦那の会社が傾いている
とか、
いろんなシチュエーションででてくる「傾き」。
一次関数ではどういう意味なんだろう？？
1次関数の「傾き」とは端的にいうと、
一次関数の「変化の割合」
のことだ。
もっとわかりやすくいうと、
xが1増えたときにyが変化する量
のことなんだ。
たとえば、y= 2x + 1っていう一次関数だったら、
xが1増えたらyが2増えるでしょ？？
だから、傾き（変化の割合）は「2」なのさ。
1次関数の傾きがわかる2つの求め方
今日は「傾き」を求める方法をつぎの2つ紹介するよ。
よかったら参考にしてみてね。
求め方1. 数式から「xの項の係数」をさがす
一次関数の数式中で、
xがついた項の係数が「傾き」
なんだ。
つまり、
1次関数 y= ax + b のaが「傾き」ってわけさ。
たとえば、つぎのような問題があったとしよう。
つぎの直線の傾きをいいなさい。
y = -5x + 9
この手の問題もぜんぜんあわてることはない。
ただ、数式をみて、
xの項についている係数
を答えればいいんだ。
そいつが「傾き」さ。
例題でいうと、
xの項は「-5x」。
こいつの係数は「-5」。
ってことは、傾きは「-5」ってわけ。
ね？一次関数をみるだけで傾きがわかったでしょ！？
求め方2. グラフから「傾き」をよみとる方法
グラフのから傾き（変化の割合）を読み取っちゃう方法だ。
1次関数上の2点をえらんで、
- xの増加量
- yの増加量
を読み取る。
そのあとに、変化の割合の公式で「傾き」をだしてやればいいんだ。
たとえば、つぎのような例題があったとしよう。
つぎの一次関数の傾きを求めなさい。
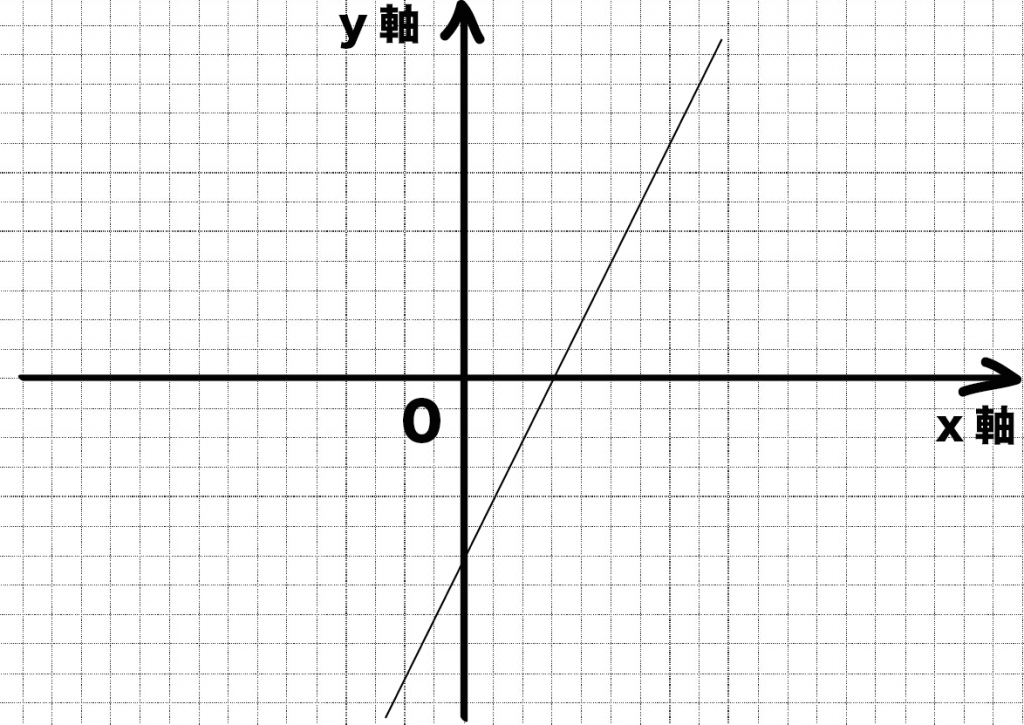
この手の問題は、
一次関数上で「2つの整数のポイント」をさがすから始めるよ。
例題の一次関数は、
- （3, 0）
- （4, 2）
っていう2つの整数の点を通っているね。
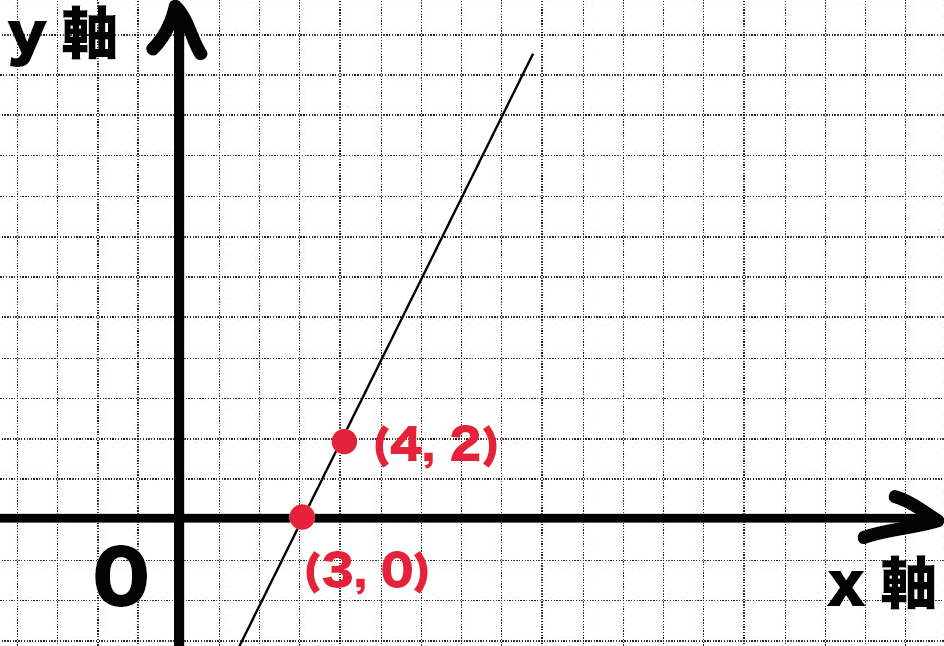
この2点間で、どのようにx・yの値が変化しているのかというと、
xが1増えたら、yが2増える
って変化しているでしょ？？
ってことは、
この一次関数の変化の割合（傾き）は、
＝ 2 ÷ 1
＝ 2
になるね。
グラフから傾きを読み取る問題は、
xがいくつ増えたら、yがどれくらい変化するのか？？
ということを確認しよう！
まとめ：一次関数の傾きは2つの求め方で十分！
傾き、すなわち変化の割合は、
- 1次関数の式から「a」をみつける
- グラフから変化の割合を計算する
の2通りでゲットできるよ。
あとは、テスト前に問題になれてみてね。
そんじゃねー
Ken
