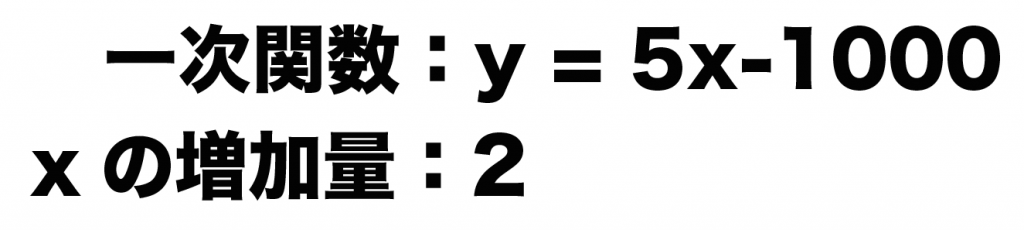一次関数のx・yの増加量の求め方がわからん！
こんにちは！この記事をかいているKenだよ。パスタ、うまいね。
一次関数を勉強していると、
xの増加量を計算して？
とか、
yの増加量を求めねえと・・・
みたいなこと多いよね。
うん、これ、つらいよ。
今日はそんな事態にそなえて、
1次関数における「xの増加量」と「yの増加量」の求め方
を2つ紹介するよ。
1次関数で増加量がわかる2つの求め方
増加量の求め方には2つのパターンがあるんだ。
「xとyの変化前後の値がわかっている場合」
1つ目のパターンは、
xとyの「変化前」と「変化後」の値がわかっているヤツだ。
たとえば、つぎのような問題だね。
xが3から6に変化したとき、yの値が8から-1になる一次関数があったとしよう。
このとき、xの増加量とyの増加量を求めなさい。
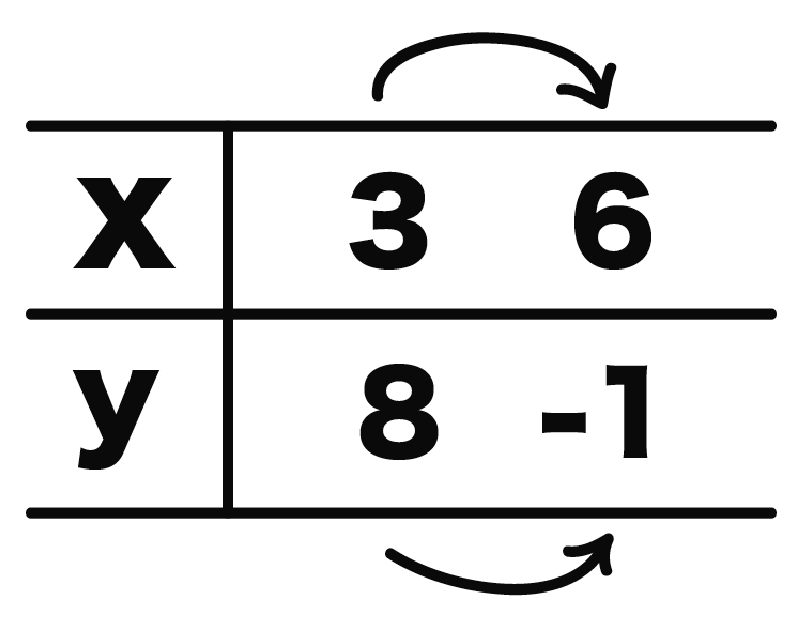
この問題では、
（変化後の値）- (変化前の値)
で計算してやればいいんだよ。
まずはxの増加量を求めてみよう。
xは「3」から「6」まで変化しているよね？？
つまり、
- 変化前のx → 3
- 変化後のx → 6
ってわけだ。
これを、
（変化後の値）- (変化前の値)
で計算してやると、
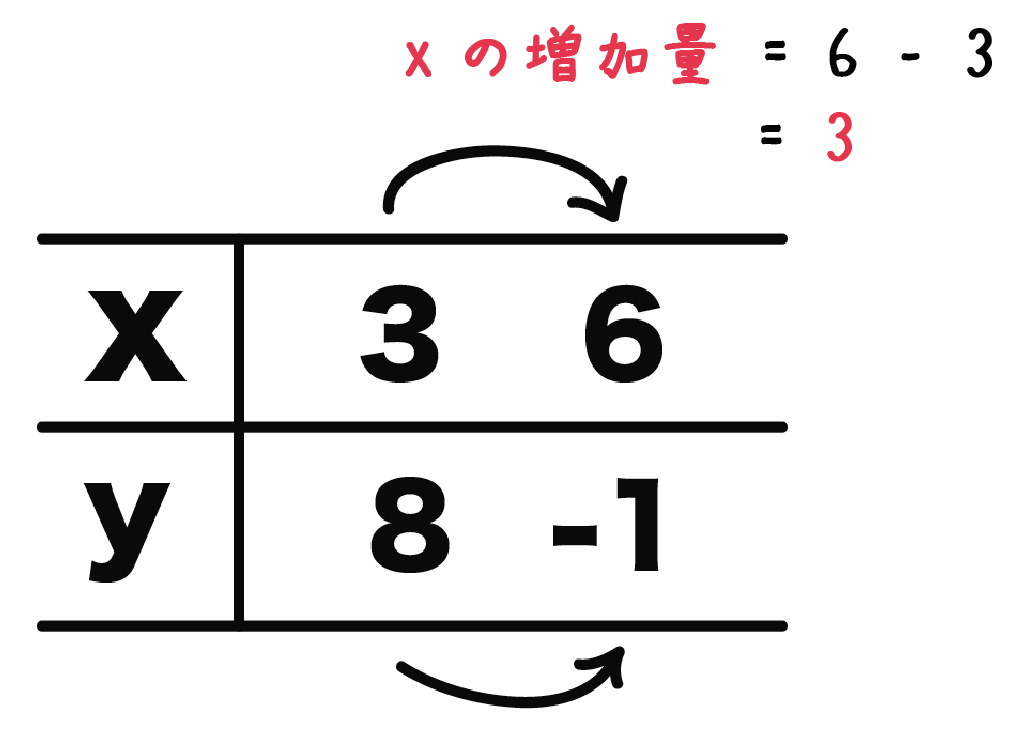
6 – 3
= 3
になるね！
yの増加量も同じ方法で求められるよ。
（変化後の値）- (変化前の値)
だから、
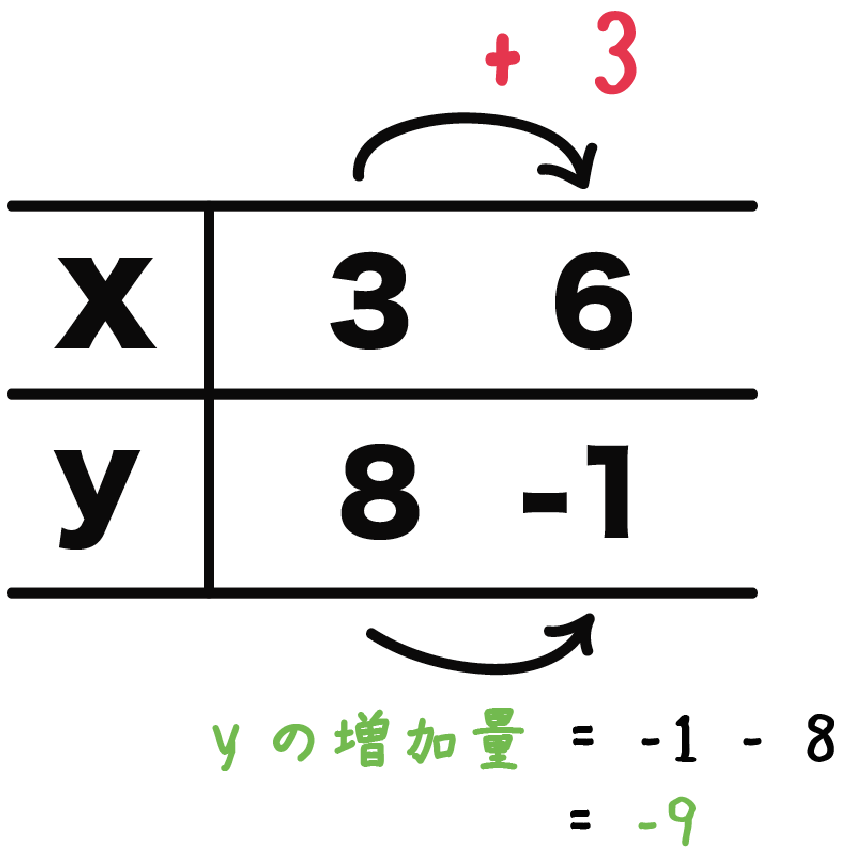
（yの増加量）= -1 – 8
= -9
になるね。
これが一番シンプルな増加量の求め方。
基本だからしっかりおさえておこう。
「変化の割合」と1つの「増加量」がわかってる場合
2つめのパターンは、
1次関数の「変化の割合」と「増加量」がわかってるヤツだ。
わかってる「増加量」は「x」でも「y」のヤツでも構わないよ。
たとえば、つぎのような問題だ。
一次関数 y = 5x – 10000 で、xの増加量が2のとき、yの増加量を求めよ。
この手の問題は、
変化の割合 = (yの増加量) ÷ (xの増加量)
の公式をつかうよ。
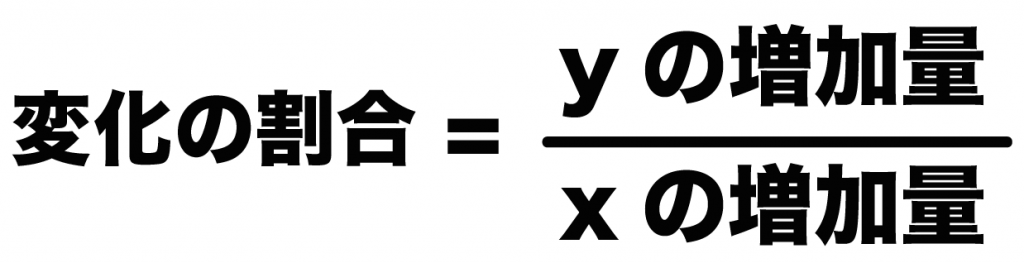
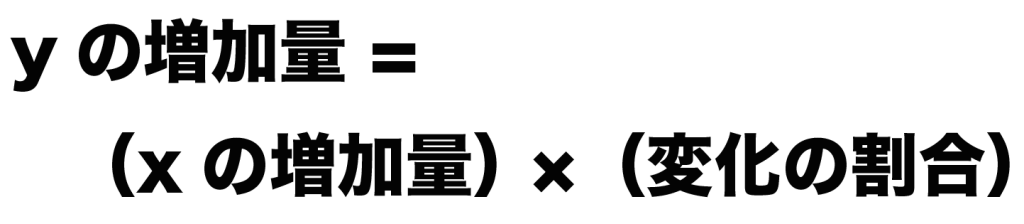
等式の変形で「yの増加量=」のカタチに変えてやると、
（yの増加量）＝ （変化の割合）×（xの増加量）
になるよね？？
y = 5x -1000の「変化の割合」は「5」。
xの増加量は「2」。
ってことは、yの増加量は、
（yの増加量）＝（変化の割合）×（xの増加量）
＝ 5 × 2
＝ 10
になるね。
公式を変形して計算するだけさ！
xの増加量も同じようにやってみてね。
まとめ：1次関数の増加量の求め方は2パターン!!
一次関数でx・yの増加量を求める問題は、
- 変化前後の値を引き算する
- 公式を変形させて計算する
の2パターン。
これでだいたいイケルね。
あとは問題をときまくって、一次関数の問題になれてみよう。
そんじゃねー
Ken
