中学数学で役立つ!円周角の3つの性質
円周角の性質は3つもあるの!?
こんにちは!ぺーたーだよ。
この前は、円周角の定理とはなにか??
ってことを勉強してきたよね。
今日はもう一歩ふみこんで、
円周角の性質
をまなんでいこう。
中学数学で勉強する円周角の性質は、
ぜんぶで3つ。
3つ覚えておけばいろんなとこで活躍するよ。
「できれば覚えておいてほしい」というよりは、
「絶対言えるようになってね!」っていう内容だね。
どんな性質なのか見ていこう!
中学数学で役立つ!円周角の3つの性質
中学数学で役に立つ「円周角の性質」はつぎの3つだよ。
- 同じ弧に対する円周角は等しい
- 等しい弧に対する円周角は等しい
- 半円の弧に対する円周角は90°
それぞれ順番にみていこうか。
性質1. 「同じ弧に対する円周角は等しい」
これは円周角の定理の復習。
円周角の定理に、
同じ弧を共有してる円周角はどれも等しい
っていうやつがあったよね。
これはね、円周角の問題を解く時によくでてくるから、
絶対におさえておきたい性質だね。
たとえば、つぎの円Oがいたとしよう
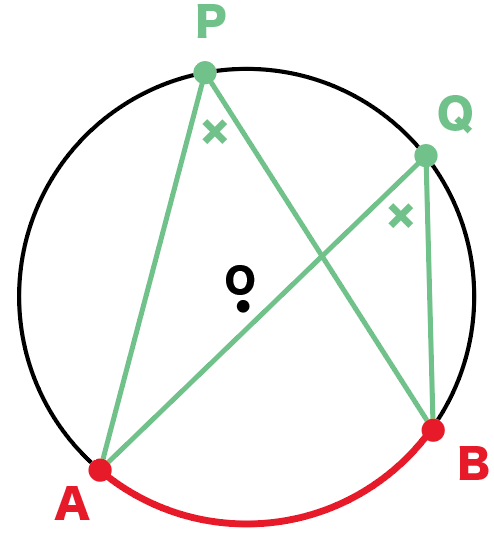
このとき、
角APBと角AQBは、
弧ABの円周角だよね??
さっきでてきた円周角の定理をつかうと、
角APB = 角AQB
ってことがいえるんだ。
たとえば、角APBが50°だとすると、
角AQBもおなじ50°になるわけ。
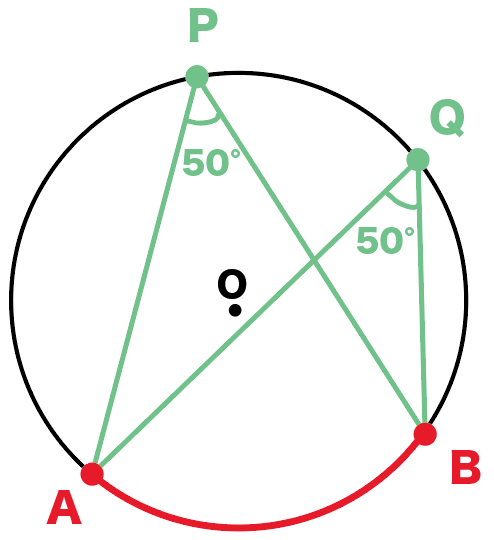
これは円周角の問題では絶対に知っておきたい性質だね。
性質2. 「等しい弧に対する円周角は等しい」
2つ目の円周角の性質は、
等しい弧の円周角は等しいよ
ってやつね。
円周角の問題でむちゃくちゃよく使うよ。
たとえば、つぎの下の円をイメージしてみて。
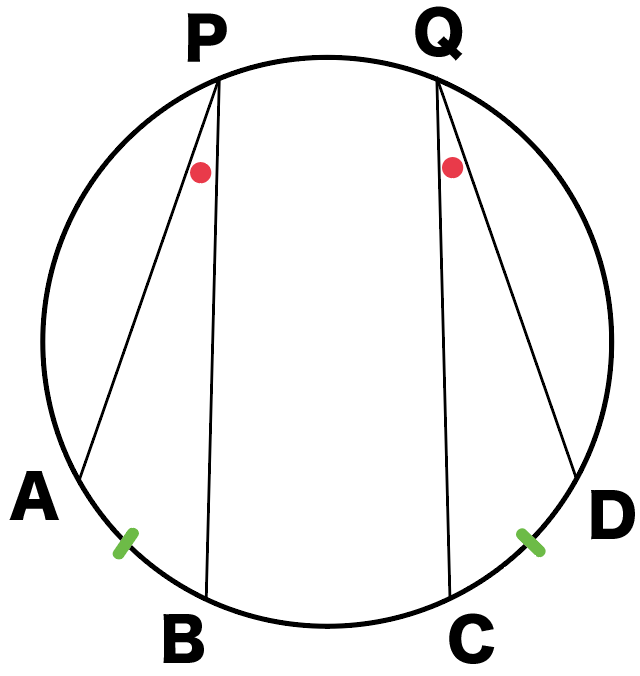
円周上に弧ABと弧CDがあるよね。
それぞれ円周角∠APB、∠CQDがあるけど、
2つの弧の長さが等しいとき(弧AB=CD弧)、
円周角も同じ大きさになるっていう性質だよ。
つまり、
∠APB=∠CQD
がいえるんだ。
だから、
∠APB=30°だとしたら、
∠CQDも30°になるってわけ。
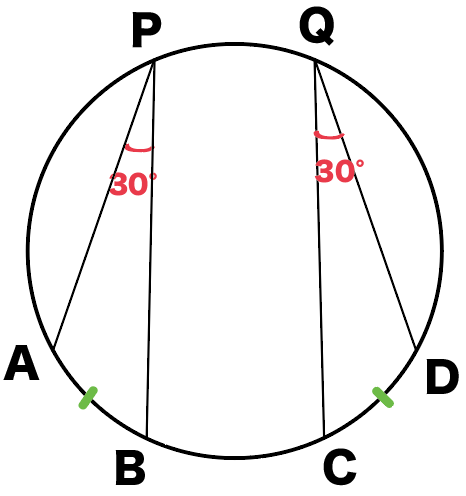
この円周角の円周角の性質はちらっとでてくることがあるよ。
よく復習しておこう。
性質3. 「半円の弧に対する円周角は90°」
いよいよ最後の円周角の性質。
もし、弧が半円のやつだったら、そいつの円周角は、
90°になる
っていう性質だね。
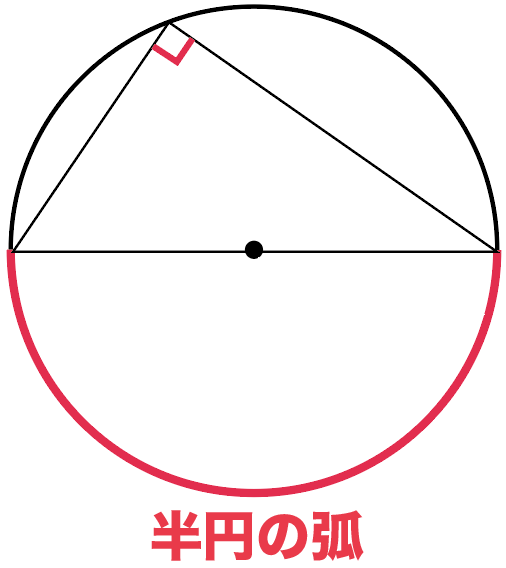
「えっ、そうなの!?」
ってびっくりする人もいるかもしれない。
これも、知っているのと知らないのとでは
問題を考えるときに大きな違いが出てくるから
ぜひ覚えておきたいところだね!
図で表すとこんな感じだ。
たとえば、下の円Oを想像してみて。
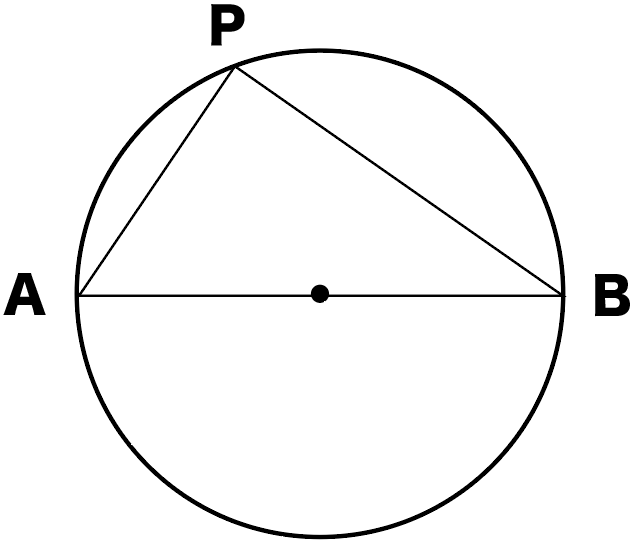
直線ABは中心Oを通ってるから、
円の直径になってるよね。
直径ABで円を切ると半円になるから、
弧ABは半円の弧になってることがわかる。
よって、
半円の弧に対する円周角の角APBは90°になってるわけ。
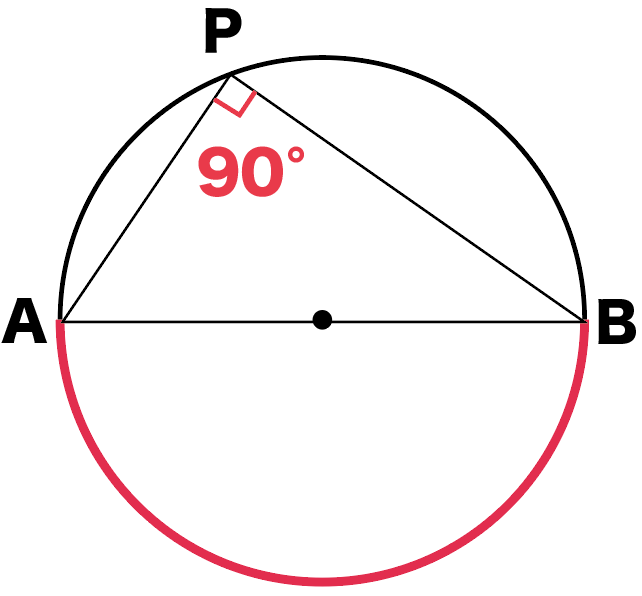
えっ。なんで半円の弧に対する円周角が90°になるのかって??
って人のために、
なぜ、半円の孤に対する円周角は90°になるのか
を説明しておこう。
って言っても、これ自体はめちゃ簡単。
円周角の定理をつかえば説明できちゃうんだ。
半円の弧に対する中心角
に注目してみて。
さっきの弧ABに対する中心角をみてみると、
直線ABがつくる180°
であることがわかるね。
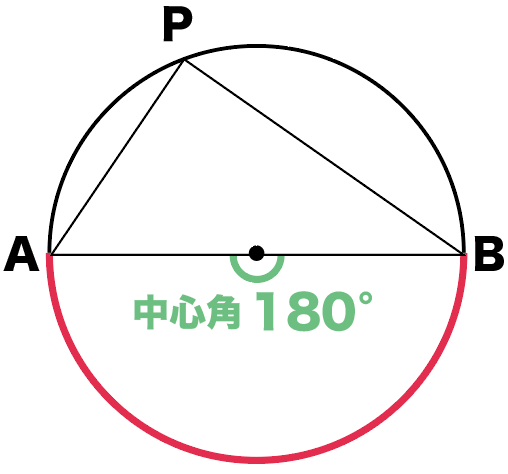
で、あとは円周角と中心角の関係を思い出そう。
1つの弧に対する円周角の大きさは、その弧に対する中心角の半分である
だったから、
中心角の半分の大きさが円周角になるんだ!
で、中心角の∠AOBって180°だよね?
その半分が円周角なんだから、
円周角の∠APB=90°になるんだ!
これで説明終わりだよ。
意外と簡単だったでしょ?(。)
まとめ:円周角の性質は問題をとくために必須!!
円周角の性質はどうだったかな??
ここで出てきた性質は問題を解く上では必須。
絶対忘れないようにしてね!
この円周角の性質と同じぐらい大事なのは、
だね。こっちも忘れかけてたら復習してみてね。
じゃあ、今日はこのへんで。
またね!
ぺーたー


