円周角の定理をつかった証明問題がわかる3ステップ
円周角の定理をつかった証明問題ってどう解くの??
こんにちは!ぺーたーだよ。
円周角の定理とか円周角の定理の逆とか
もう慣れてきたかな?
円周角の定理って角度を求めるときにも使うんだけど、
相似を証明するときにも使えるんだ。
たとえば、つぎみたいな証明問題ね。
練習問題
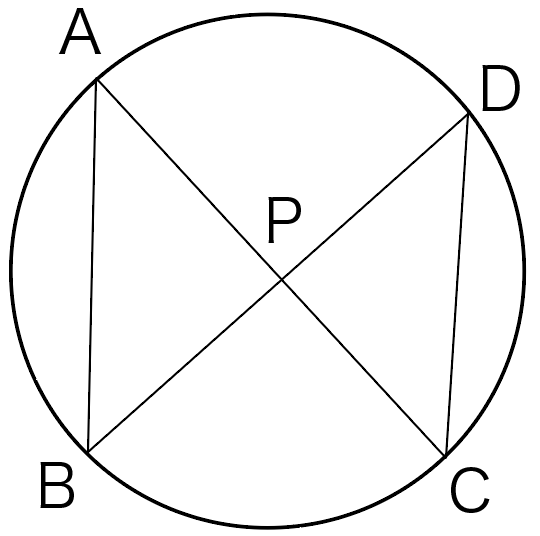
下の図のように、円周上に4点A,B,C,Dがあり、
ACとBDの交点をPとする。
このとき△ABP∽△DCPになることを証明せよ。
今日は、この問題を解説するよ。
証明に必要なことを復習しながら説明するから、
頑張ってついてきてね!
円周角の定理の証明の解き方がわかる3ステップ
円周角の定理の証明問題はつぎの3ステップでとけちゃうよ。
- 円周角の定理をつかう
- 相似条件をつかう
- 証明を書く
さっきの練習問題をといていこう。
練習問題
下の図のように、円周上に4点A,B,C,Dがあり、
ACとBDの交点をPとする。
このとき△ABP∽△DCPになることを証明せよ。

Step1. 円周角の定理をつかう
証明問題に入る前に、
円周角の定理ってなんだったか、しっかり思い出しとこう!
円周角の定理は2つの性質があったね!
1つの弧に対する円周角の大きさは、
その弧に対する中心角の半分ってやつと、
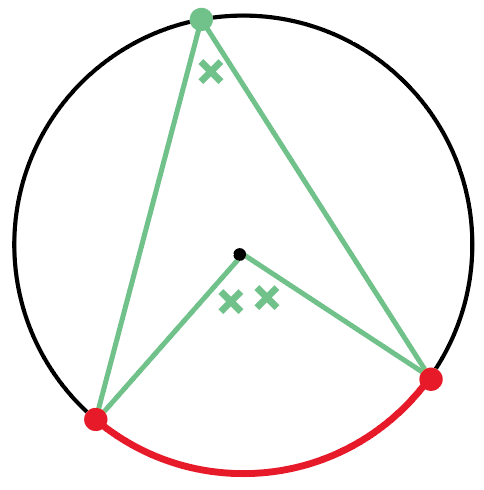
同じ弧に対する円周角の大きさは等しいってやつだね。
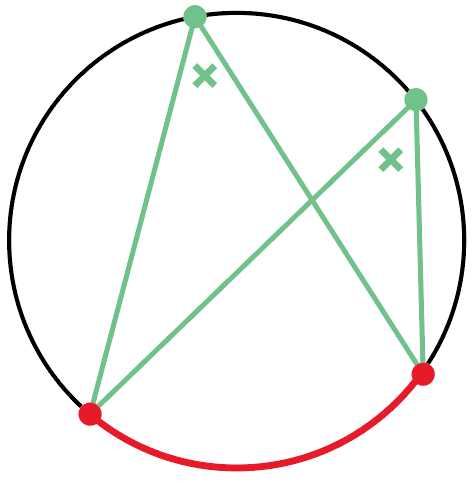
くわしくは「円周角の定理」の記事を復習してみてね。
まず、さっき思い出した円周角の定理を使って、
等しい角がないか確かめてみよう。
弧BCの円周角がどこになるかわかるかな?
そう。
∠BACと∠BDCだね!
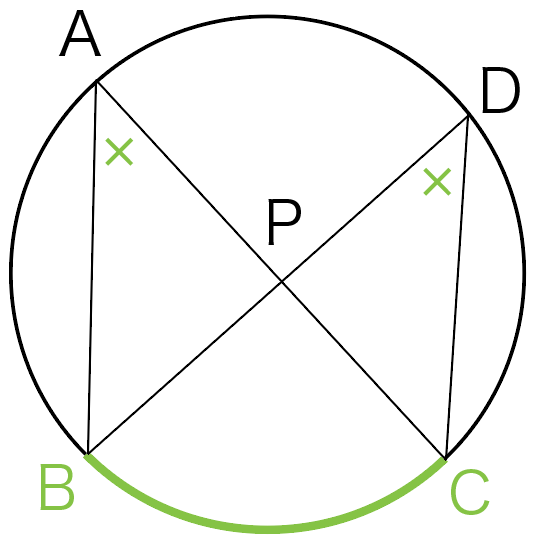
1つの弧に対する円周角は等しいんだから、
この2つの角は等しいってことになるね!
∠BAC=∠BDC…①
もう1つの角も円周角が使えるよ。
今度は弧ADで見てみようか。
さっきと同じように円周角を見つけてよう。
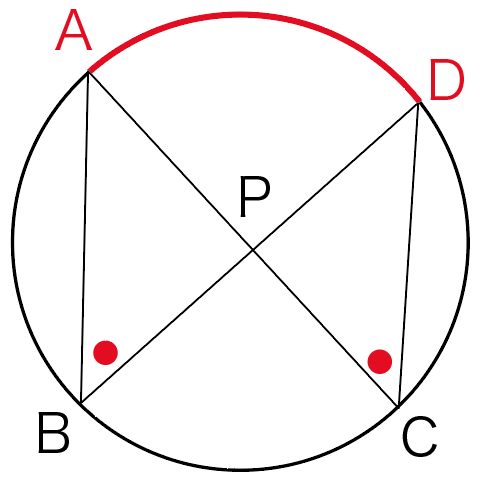
そうすると2つの円周角が見つかるね!
ってことは角の大きさは一緒だね!
∠ABD=∠ACD…②
Step2. 相似条件をつかう
つぎは相似条件で三角形の相似を証明しよう。
相似条件は、
- 2つの角がそれぞれ等しい
- 3辺の比がそれぞれ等しい
- 2辺の比とその間の角がそれぞれ等しい
だったね??
円周角の定理の証明では、十中八九、
2組の角がそれぞれ等しい
をつかうかな。
なぜなら、円周角の定理では辺の比が等しいことは証明しにくいからね。
角度が等しいことなら得意分野なんだ。
だから、まずは、
2組の角が等しいことがいえるかどうかを疑ってみよう。
練習問題をみてみて。
Step1で円周角の定理をつかったら、
- ∠BAC=∠BDC…①
- ∠ABD=∠ACD…②
がわかったよね??
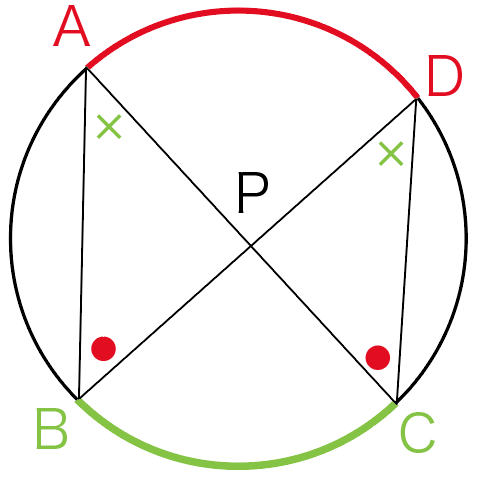
ってことは、
△ABPと△DCPにおいて、
2組の角が等しいことがいえるね。
よって、これは相似条件をみたしてるから、
△ABP∽△DCP
がいえるってわけね。
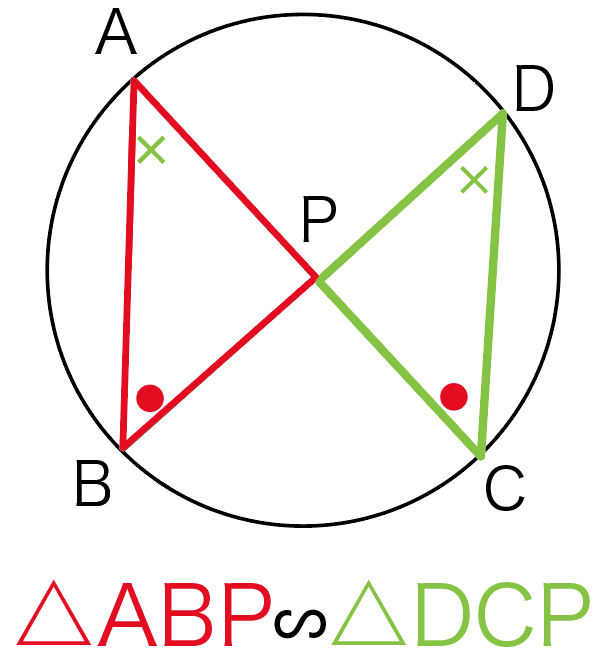
これで証明のゴールにたどり着けたね!
Step3. 証明をかく
証明のゴールまでの見通しができたら、
あとは証明をかくだけ。
相似の証明の書き方を参考にしてね。
Step2までのながれをかいてみるとこうなるね↓↓
△ABPと△DCPについて、
円周角の定理より、同じ弧に対する円周角は等しいので、
∠BAC=∠BDC…①
∠ABD=∠ACD…②
①、②より、
2組の角がそれぞれ等しいので、
△ABP∽△DCP
ってかんじかな!
まとめ:円周角の定理を使って等しい角を見つけ出そう
円周角の定理をつかった証明問題はどうだった??
基本的な解き方としては、
円周角の定理をつかって、
相似条件の「2組の角がそれぞれ等しい」の方向に持ち込む・・・
というのが基本かな。
今回紹介した証明問題は、基本的なものあったけど、
応用問題でも構造はいっしょ。
円周角については問題をたくさん解いて、
「こことここは円周角の定理で等しいな」
って見つけられるのが一番かな!
今日はこれでおしまい!
またね!
ぺーたー


