円周角の定理で角度を求める問題が苦手！
こんにちは！ぺーたーだよ。
中3数学の「円の性質」では、
を勉強してきたね。
今日はこいつらを使って、
円周角で角度を求める問題
にチャンレジしていこう。
円周角の定理をむちゃくちゃ使うから、
「まだよくわかんない…」っていう人は、
円周角の定理を復習してみてね。
円周角の定理をつかって角度を求める3つの問題
さっそく、円周角で角度を求める問題をといていこう。
テストで役立つ3つの問題をいっしょにといてみよう。
円周角を求める問題1.
つぎの円Oにおいて角度xを求めなさい。
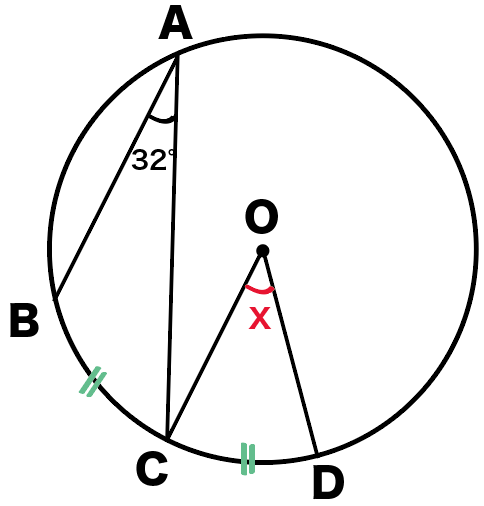
ただし、
孤BC = 孤CDとします。
この問題では、円周角の性質の、
1つの円で等しい弧に対する円周角の大きさは等しい
をつかっていくよ。
孤BC = 孤CDだから、
孤BCと孤CDがつくる円周角は等しいはずだね。
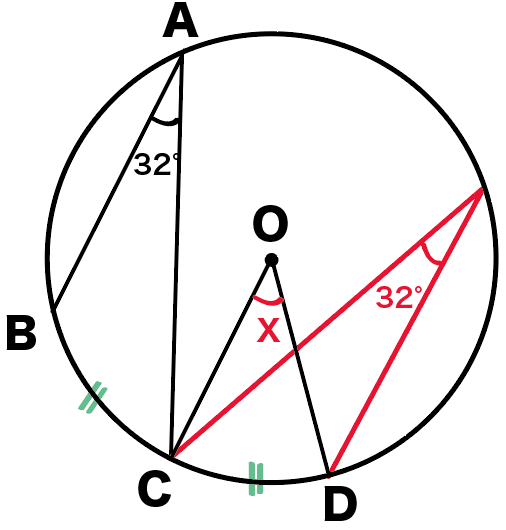
ってことは答えはもう簡単！
弧BCの円周角BACが32°だから、
弧CDの円周角も32°ってことだね！
でも、問題で求めたい角xは、
孤CDの円周角じゃなくて中心角だ。
円周角の定理より、
同じ孤の円周角を2倍すると中心角になるんだったね？？
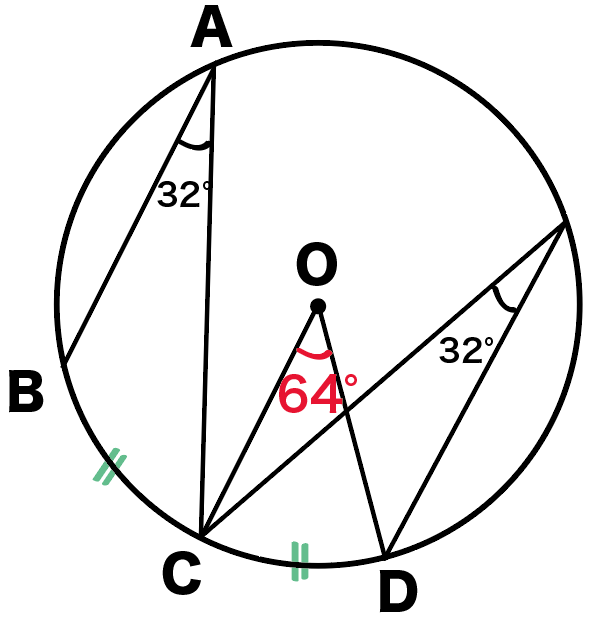
ってことは、角xは円周角32°を2倍した、
∠x = 64°
になるはず。
円周角を求める問題2.
つぎの円Oにおいて角xを求めなさい。
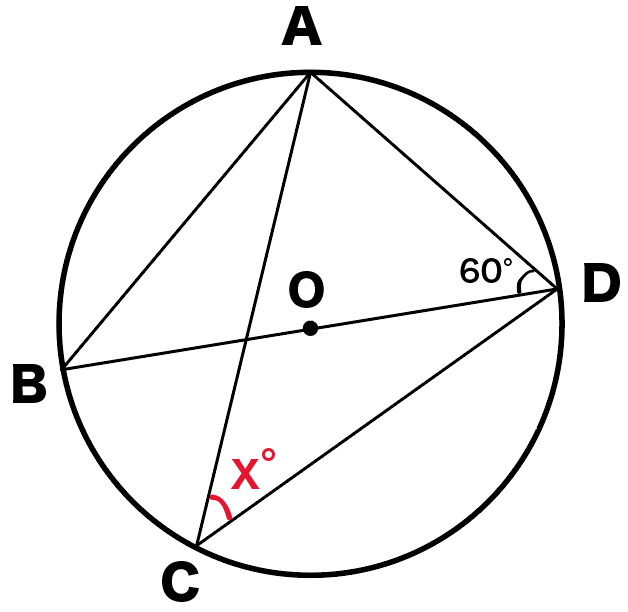
この問題では、
- 円周角の定理
- 円周角の性質
をフルフルにつかっていくよ。
まず、円周角の性質の、
半円の孤に対する円周角は90°
ってやつをつかってみよう。
円周角BADは半円に対する円周角だから、
∠BAD = 90°
になるね。
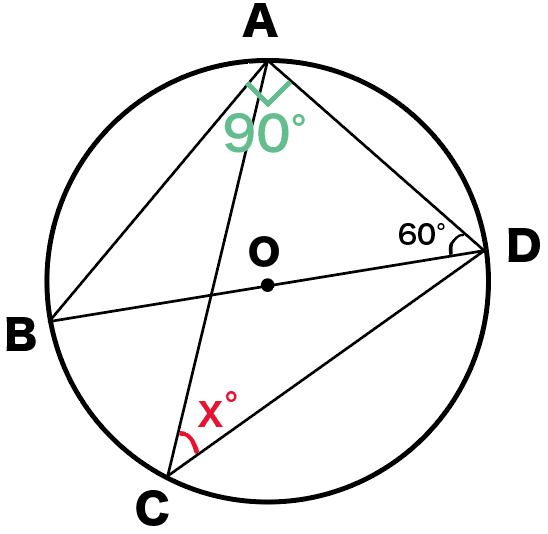
んで、ここで△ABDに注目してみよう。
三角形の内角の和は180°だったよね？？
△ABDの内角のうちの2つの、
- ∠BAD = 90°
- ∠ADB = 60°
がわかってるよね？？
ってことは、残りの内角の∠ABDは、
∠ABD
= （三角形の内角の和）- （∠BAD + ∠ADB )
= 180 – (90+60)
= 30°
になるね！
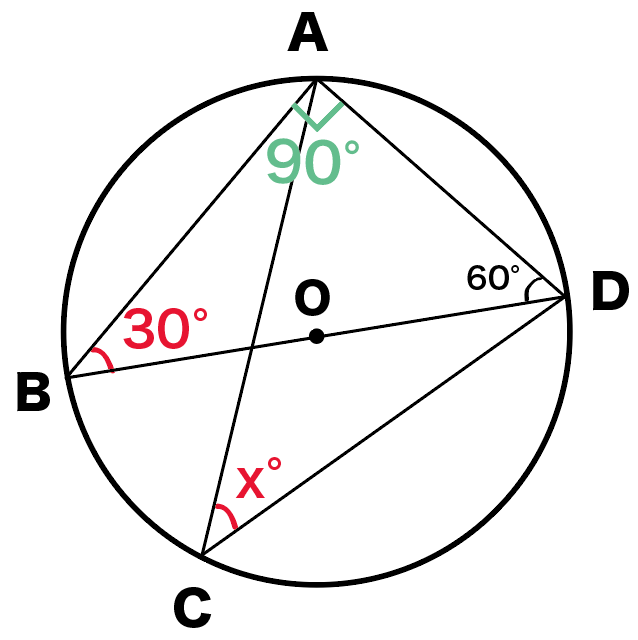
つぎは、円周角の定理をつかうね。
同じ弧に対する円周角は等しい
っていう定理をつかうと、
∠ABD = ∠ACD = 30°
になるね。
なぜなら、
両方とも孤ADに対する円周角だからね。
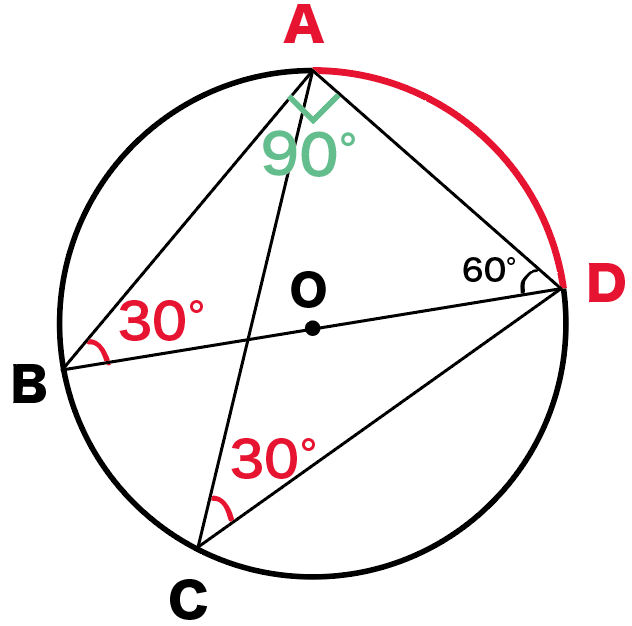
ってことで、
xは30°ね！
円周角を求める問題3.
つぎの円Oにおいて∠xを求めなさい。
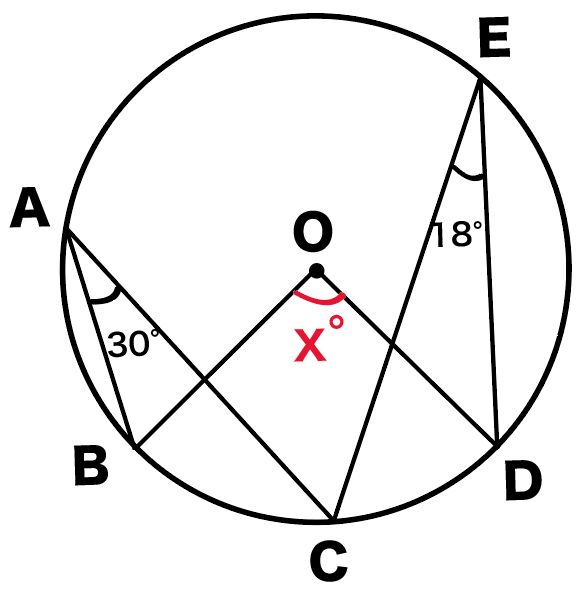
次はちょっと手ごわそうだねー。
こいつはこのままだと答えまで出すのは
難しいかもしれないね。
だから、自分で線を1本足してあげよう。
どこに付け足すかわかるかな?
そう。そうだよ。
AとDをむすんでみて！
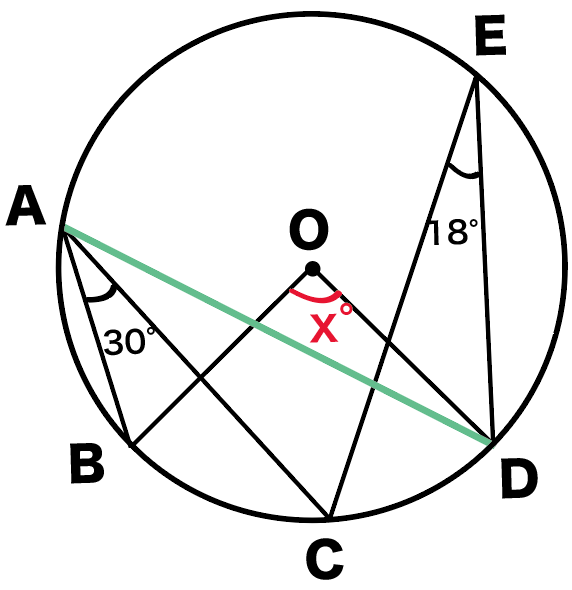
この1本の補助線が答えまで案内してくれるよ！
同じ弧の円周角は等しいんだったよね？
ってことは、
∠CED = ∠CAD = 18°
になるね。
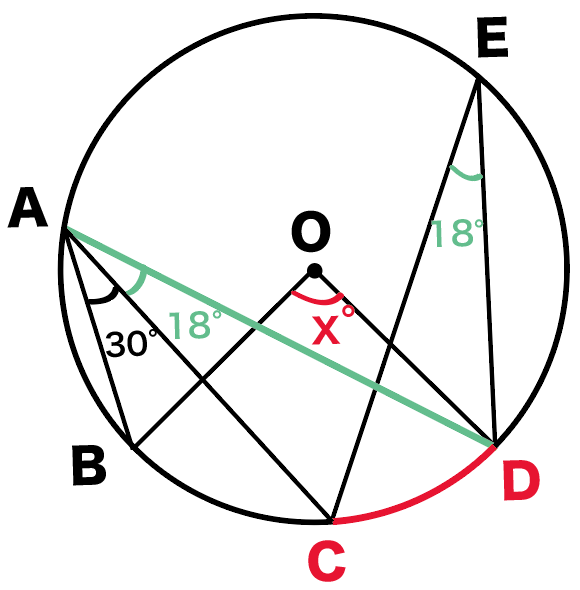
そうすると今度は、
∠BAD = 48°
になるね。
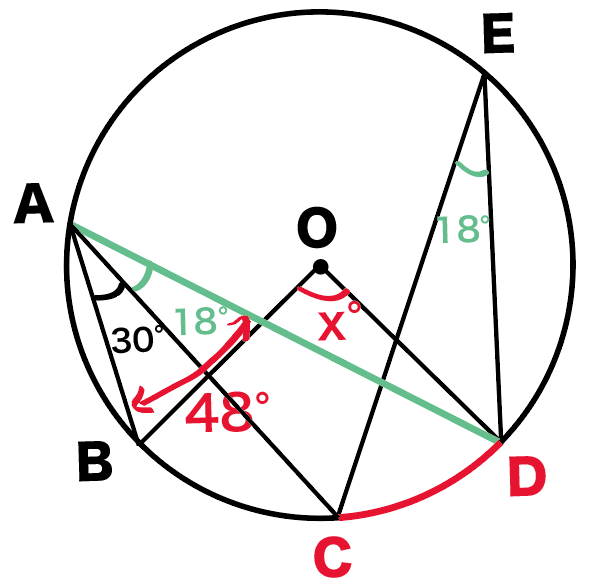
∠BADは求めたい∠BODの円周角。
ってことは、
円周角の定理の、
1つの弧に対する円周角の大きさは、
その弧に対する中心角の半分
ってやつをつかえばいいね。
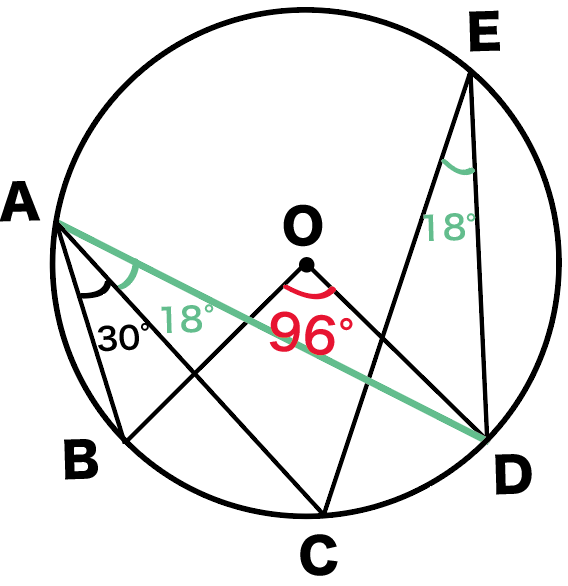
すると、
x= ∠BAD×2
= 48°×2 = 96°
になるね！
まとめ：円周角の定理でがしがし問題をといてこう！
円周角の角度の問題はどうだった？？
最初は慣れないかもしれないけど、
とけると面白いはず。
円周角を求める問題が出てきたら、
解いてみるといいね！
じゃあ、今日はここまで！
ぺーたー
