【中2数学】分数がふくまれる等式の変形の2つの解き方
分数がふくまれる等式の変形はむずい??
こんにちは!この記事をかいているKenだよ。10円玉募金をはじめたね。
分数がふくまれる「等式の変形」ってむずかしいよね。
整数だけでもヤッカイなのに、分数がはいったらもっとヤバい。
そこで今日は、
「分数がふくまれている等式の解き方」をわかりやすく解説していくよ。
分数がふくまれる「等式の変形」には2つのパターンがあるんだ。
- 分母を払うパターン
- 通分するパターン
等式の変形の解き方1 : 「分母を払うパターン」
まず1つ目は分母を払うパターンだ。
これは「求める文字」が分子にあるタイプだね。
たとえば、
つぎの等式をaについて解きなさい。
a/2 + b/5 = 2
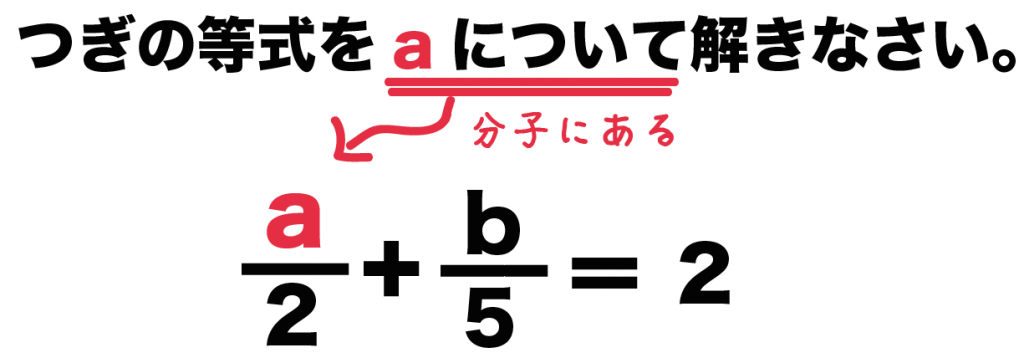
っていう問題だ。
これは、
○○について解きなさい
っていう○○の文字が分子にはいっているよね。
このタイプの問題はつぎの3ステップでとけちゃうんだ。
Step1. 分母をはらう!!
まず分母をはらっちゃおう。
等式から分数を消せちゃうってわけ。
つまり、
分母の最小公倍数を等式全体にかけてやればいいのさ。
例題でいうと、
分母の「2」と「5」の最小公倍数は「10」だよね。
こいつを等式の両辺にかけてみると、
10×(a/2 + b/5) = 2 × 10
5a + 2b = 20

になるね!
Step2. 「求める文字」を左に移項させるっ!
分母をはらった??
そのつぎは移項だね。
「求めたい文字」を左辺に移動させよう!
それ以外は反対の右辺におしこんでね。
例題でいうと、
等式で求める文字は「a」だったよね??
ってことは「a」をふくむ項を左に、ソレ以外の項を右によせてやろう!
すると、
5a + 2b = 20
5a = 20 -2b
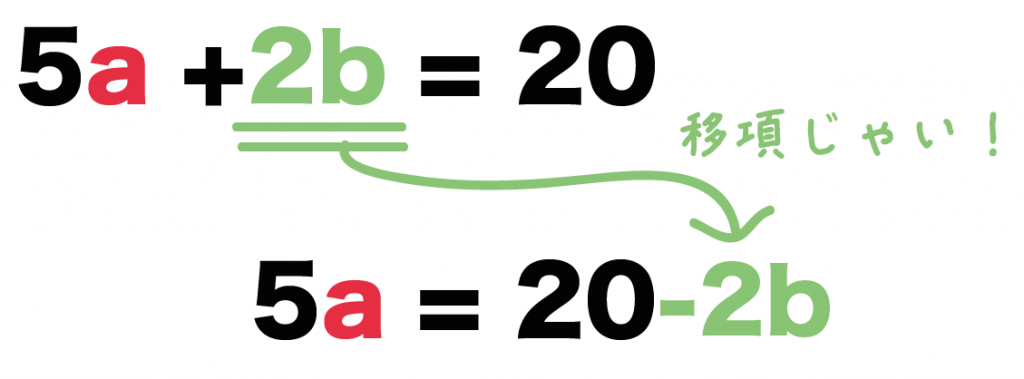
になるね!
移項するときに、項の符号が変わることに注意してね。
Step3. 求める文字の「係数」でわる!
最後は「求める文字」の係数をとってあげよう!
求める文字の前についている「数字」が係数だよ。
こいつで両辺をわってあげよう!
すると例題の式は、
5a ÷ 5 = (20-2b) ÷5
a = (20-2b)/5
になるね!
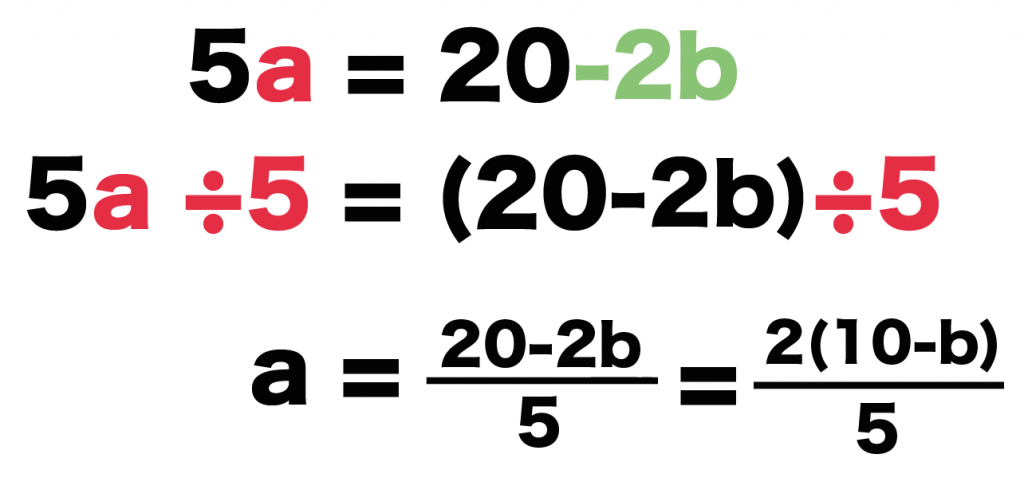
これで分母をはらうやり方はオッケーだね!!
等式の変形の解き方2:「通分するパターン」
等式の変形の2つ目のパターンは、
「求める文字」が分母にある場合だ。
たとえば次の問題のように、
つぎの等式をaについて解きなさい。
1/a + 1/b = 1/c
「〜について解きなさい」の「〜」が分母にはいっちゃっているパターンだ。
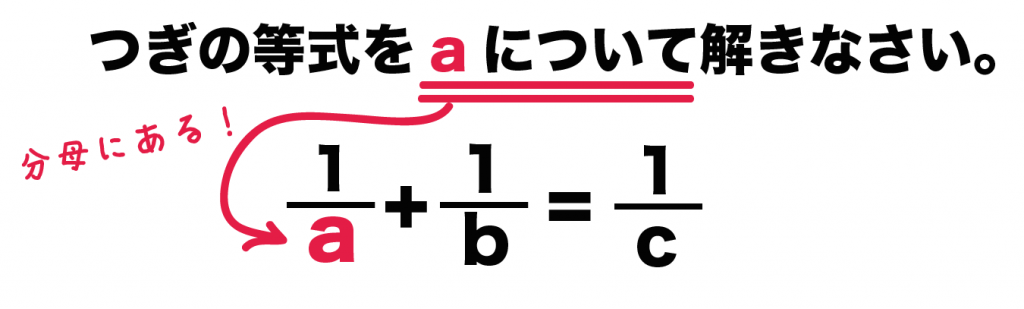
このタイプはつぎの3ステップでとけちゃうよ。
Step1. 求める文字を左に移項するっ!
「求める文字」を左辺に、ソレ以外の項を右辺によせちゃおう!
符号に注意して移項しちゃってくれ!
例題の等式では「a」が求める文字だったよね?
だから「a」を左辺に、ソレ以外の項たちを右辺によせてみよう。
すると、
1/a = 1/c -1/b
になるね!

Step2. 右辺を通分するっ!
右辺を通分して1つの分数にしてみよう!!
例題でいうと、
1/c -1/b
っていう右辺を通分してやればいいんだね。
えっ。通分のやり方がわからない!?
そんなときは「分数をふくむ文字式の通分方法」を復習してみてね。

通分してやると、
(b-c)/bc
になるね!
Step3. 両辺を逆数にするっ!
いよいよ最後のステップ。
両辺の分数を逆数にしてあげよう!!
左辺と右辺はそれぞれ1つの分数になっているから、
分子と分母を入れ替えてやればいいのさ。
例題でいうと、
1/a = (b-c)/bc
a = bc/(b-c)

になるね!
これで「通分するパターン」の解き方もマスターしたね。
おめでとう!
まとめ:分数がふくまれている等式の変形は2つ解き方だけ!
分数がふくまれている等式の変形のやり方はどうだった??
- 分母をはらうパターン
- 通分するパターン
をマスターしておけば大丈夫。
きっとテストでいい点とれるはず!本番前によーく復習しておいてね。
そんじゃねー
Ken


