円周角の定理の逆を使った問題？？
ある日、数学が苦手なかなちゃんは、
円周角の定理の逆をつかった問題が解けなくて困っていました。
練習問題
四角形ABCDで、∠x、∠yの大きさを求めなさい。
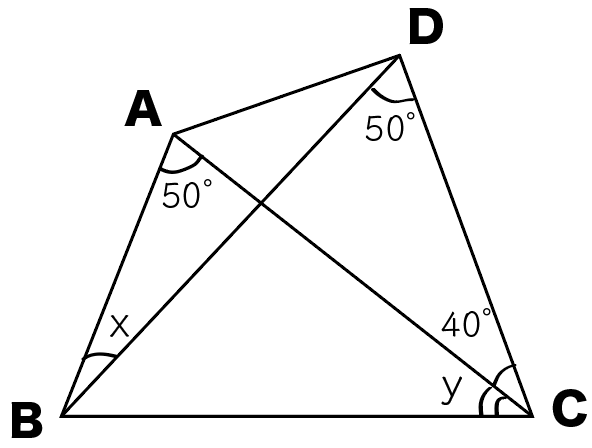
どうしよう……
どうしたの？
困ってそうだね。
やらないと友だちと遊びに行けない……
なるほど。
それは困ったね
でしょ？
この問題、角度いっぱいわかるのにムズイ！
えーっと、ふむふむ。。
おっ、これはっ……！？
これは……？
円周角の定理の逆を使えば一発さ！
え？
円周角の定理の逆の問題の解き方2つのステップ
練習問題
四角形ABCDで、∠x、∠yの大きさを求めなさい。
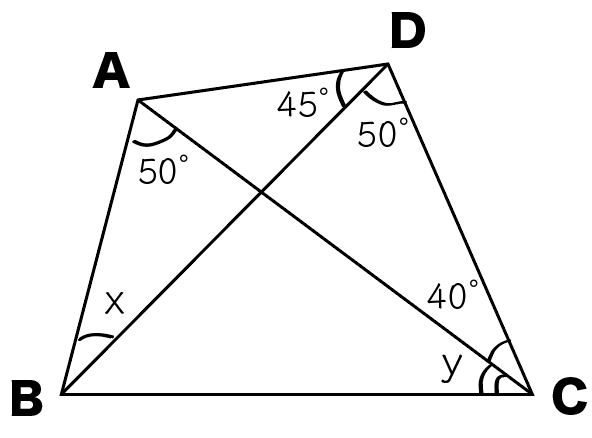
この問題では、
円周角の定理の逆をつかえばいいんだ。
えっと。。。
円周角の定理の逆ってなんだっけ？
そんなときのために用意しておいたよ
☆円周角の定理の逆☆
２点C・Pが直線ABについて同じ側にあるとき、
∠APB=∠ACBならば４点A、B、C、Pは同じ円周上にある。
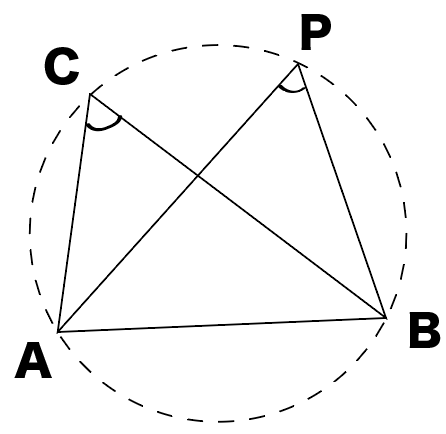
この前習ったやつだ！
だよね。
「円周角の定理の逆」を使えば2ステップで解けちゃうんだ。
- 同じ円周上にあるか確認
- 同じ弧の円周角を見つけよう
Step1. 同じ円周上にあるか確認
図形の点が同じ円周上にあるか確認しよう！
円周角の定理の逆を使ってね。
すぐに見つける方法ないの？
同じ大きさの角を見つけることかな！
同じ50度の角が2つある！！
そう！
記号で書いてみると？
∠BAC＝∠BDCでしょ？
おっ、いい感じ！
円周角の定理の逆を使ってやると、
4点A・B・ C・Dは同じ円上にあることがわかるね〜
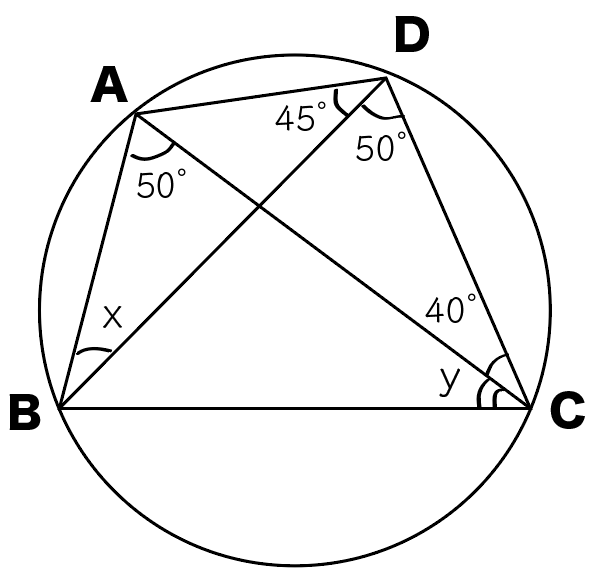
Step2. 同じ弧から作られる角度を見つけよう
同じ弧の円周角をみつけよう！
同じ弧ADの円周角みっけ！
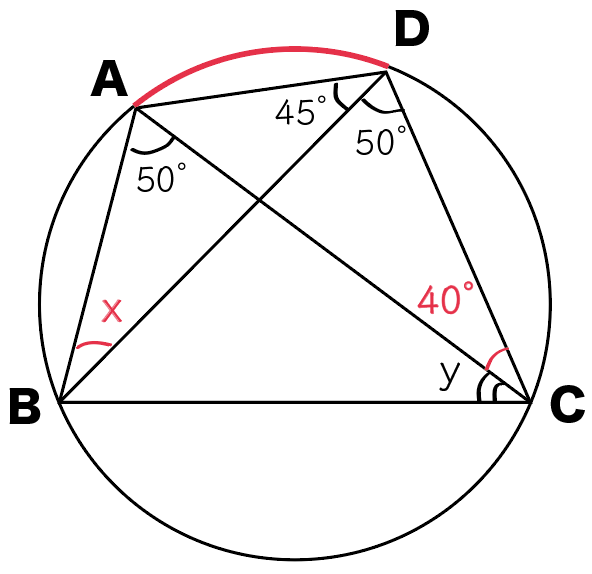
だから、
∠ABD = ∠ACD
x = 40度
になるね。
あとは、
∠ADCと∠ACB！
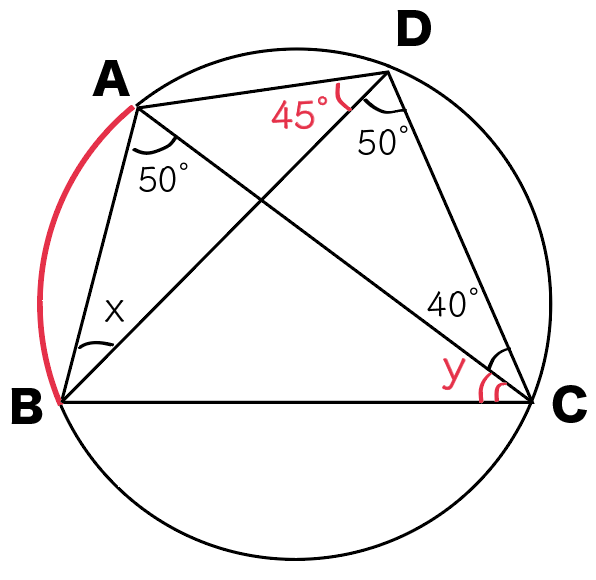
いい感じだね。
∠ADC=∠ACB
y = 45度
だ！
やったー！
まとめ：円周角の逆の定理の問題は2ステップで瞬殺
円周角の定理の逆なら2ステップで解けちゃうね。
- 同じ円周上にあるか確認
- 同じ弧から作られる角度を見つける
すぐ解けちゃうかも！！
でしょ？
1回使いこなせれば簡単！
たしかに！！
よしっ、解こう……！
あっ、友だちとの約束！！
時間をうまく使って問題を解いてみよう！！
うす！
