連立方程式の代入法の解き方をマスターしたい！
こんにちは！この記事をかいているKenだよ。肉じゃがはウマいね。
連立方程式には解き方が2つある。
- 加減法
- 代入法
だったよね？？
連立方程式の解き方でも紹介したけど、
迷ったら「加減法」をつかったほうがいいよ！
だって、簡単だからね。
だけど、
ごくたまーに、
代入法が活躍するときもあるんだ。
今日は、そんなときにそなえて、
連立方程式の代入法の解き方を解説していくよ。
よかったら参考にしてみてね。
連立方程式の代入法の解き方がわかる4つのステップ
例題といっしょに解説していくよ。
例題
つぎの連立方程式を代入法で解きなさい。
2x +3y = 14
3x + y = 0
代入法はつぎの4ステップでいいんだ。
Step1. 「係数1」の文字を左辺によせる！
どっちの式でもいい。
「係数1」の文字を左辺によせて、ソレ以外を右辺におしやろう。
係数1ってつまり、文字に何も数字がついていないってこと。
たとえば、
yとかxとかaとかね！
そうすることで、
係数1の文字 = ソレ以外
という等式に変形できちゃうんだ。
例題では、
「3x + y = 0」で「文字= ソレ以外」をつくってみよう。
「-3x」を右辺に移項してやると、
y = -3x
に変形できるね。
これで準備完了。
Step2. もう一方の方程式に代入
寄せた式をもう一方の式に代入してあげよう。
そうすることで、
方程式から文字を1つ消せるんだ。
例題でいうと、
「y = -3x」を「2x + 3y =14」に代入すればいいよ。
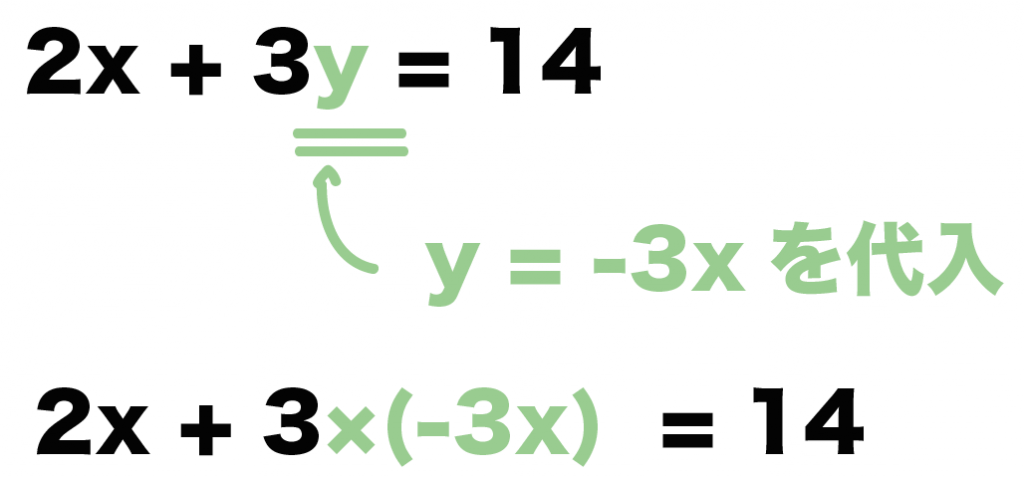
すると、
2x + 3 × ( -3x) = 14
になるね。
Step3. 一次方程式をとくっ！
代入後の方程式を実際にといてみよう！
解き方がわからんときは「一次方程式の解き方」を参考にしてね。
例題で代入した方程式を簡単にしてやると、
2x + 3 × (-3x) =14
-7x = 14
になるよね？
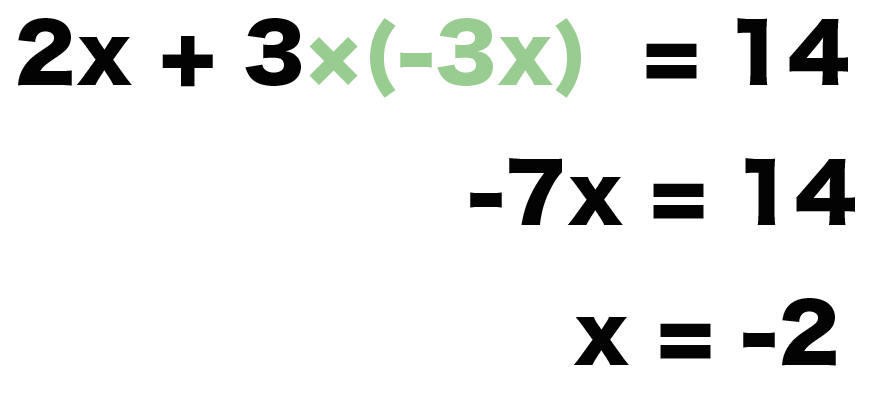
両辺をxの係数7でわってやると、
x = -2
になるよ！
Step4. ゲットした解を代入
この解を方程式に代入してあげよう。
代入する方程式はどっちでもいいよ。好きな方を選んじゃってくだせえ！
例題でいうと、xの解は「-2」だったよね？？
これを「y = -3x」にいれてみよう。
すると、
y = -3 × (-2)
= 6
という解がでてくるでしょ？？
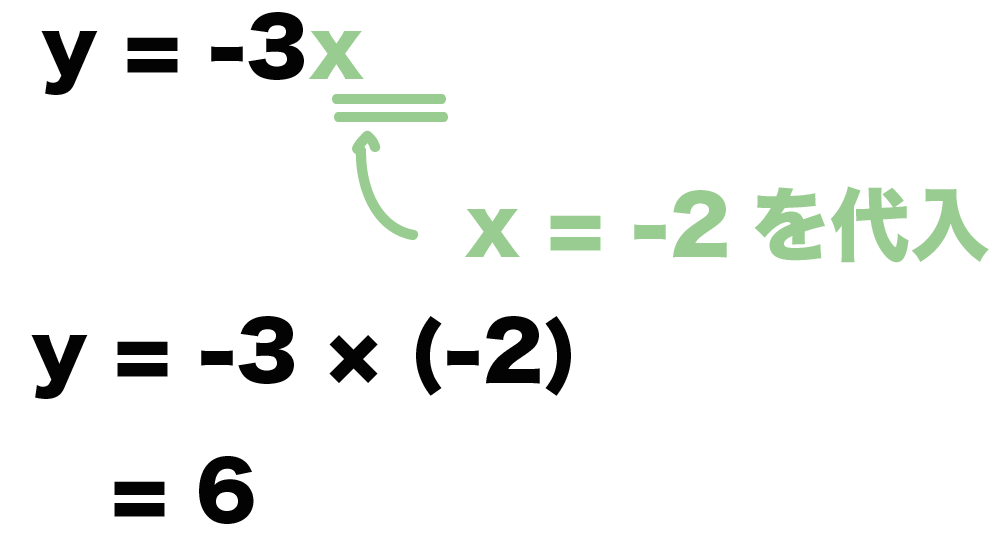
これで連立方程式の解がそろったね！
(x, y) = (-2, 6)
おめでとう！。
まとめ：連立方程式の代入法はちょっとメンドイ。
連立方程式の代入法は、
- 文字をよせる
- 代入
- 一次方程式をとく
- 代入
って感じで代入が2回もあってダルい。
だから、できれば代入法は使わないほうがいいね。
いつ、代入法をつかうべきなのか？？？
を見極めながら解き方を修得していってほしいね。
そんじゃねー
Ken
