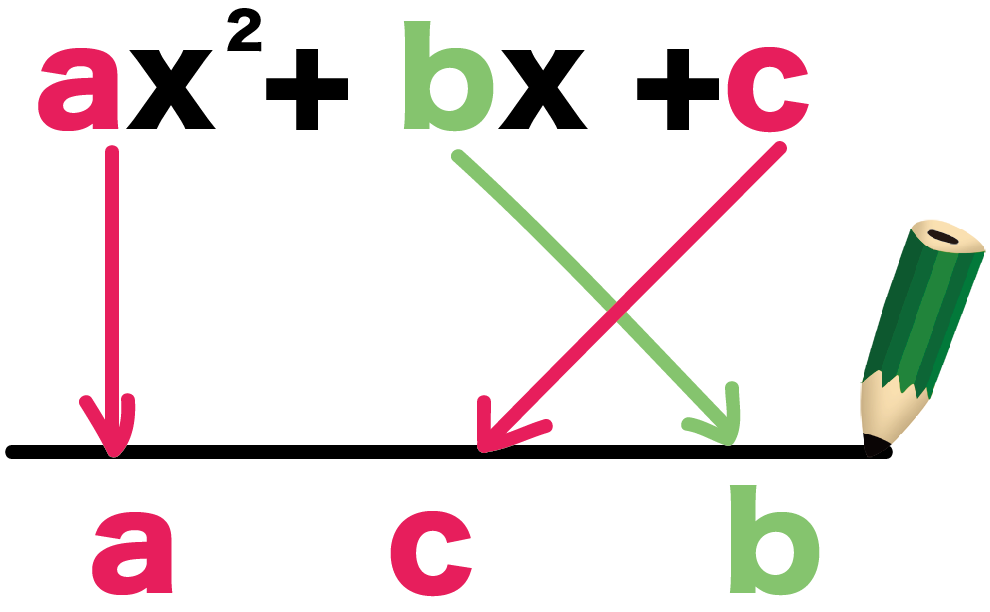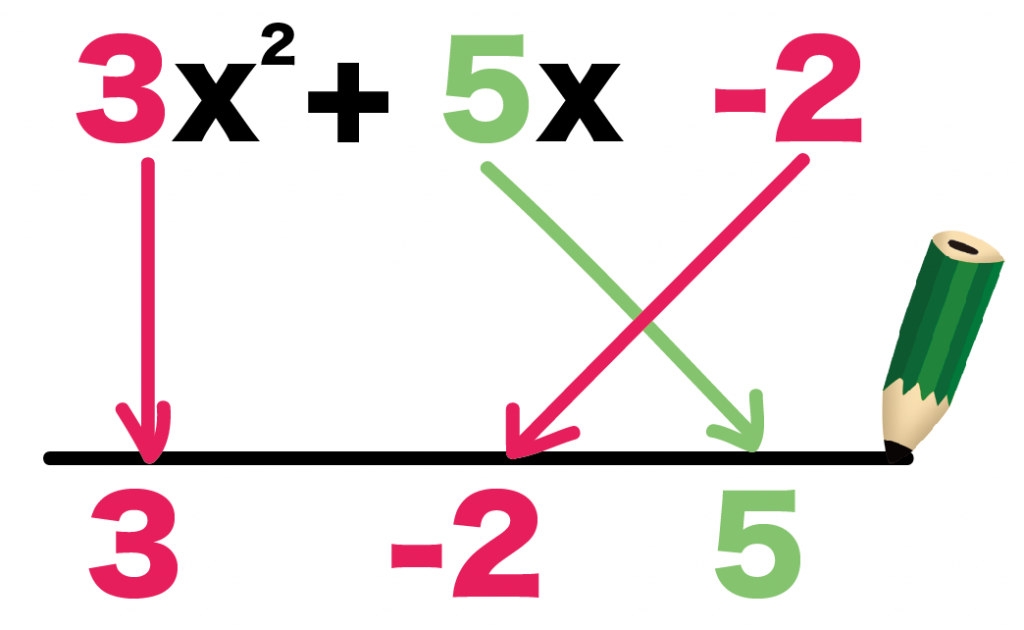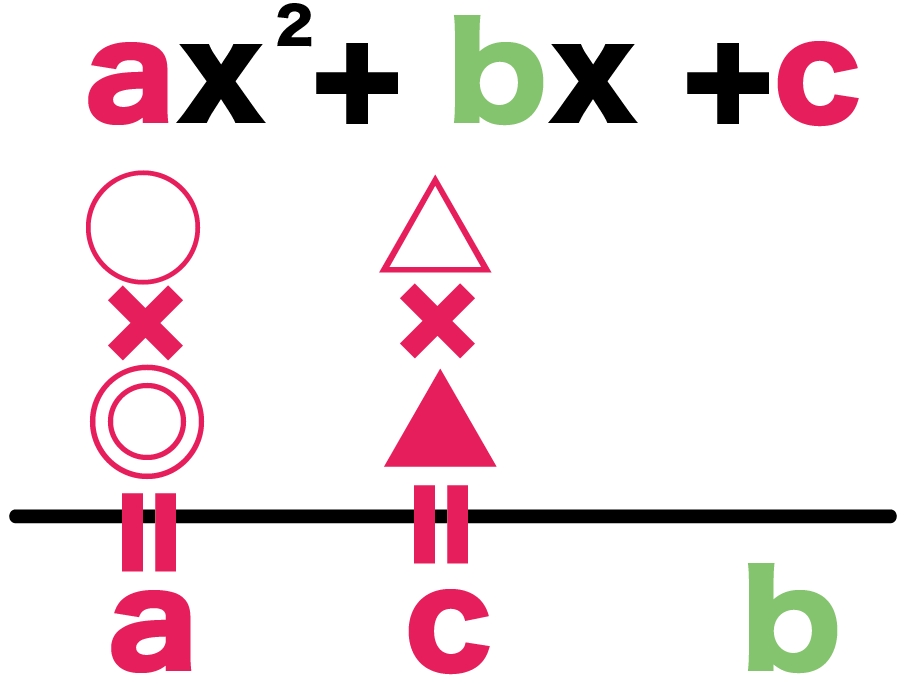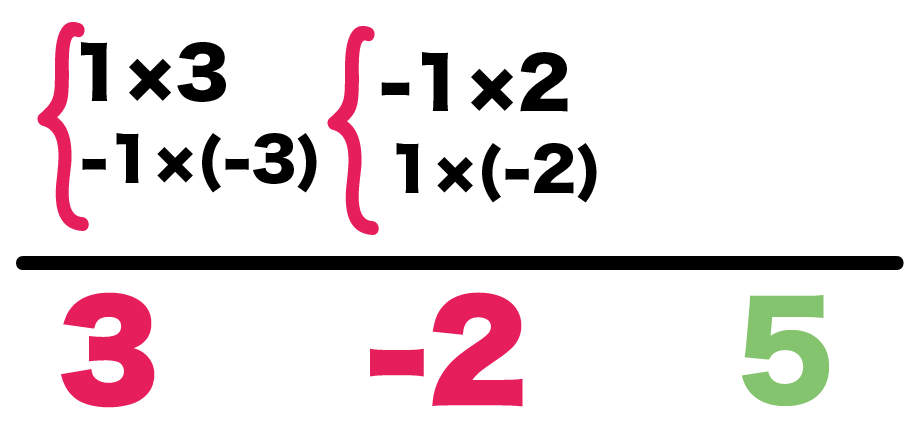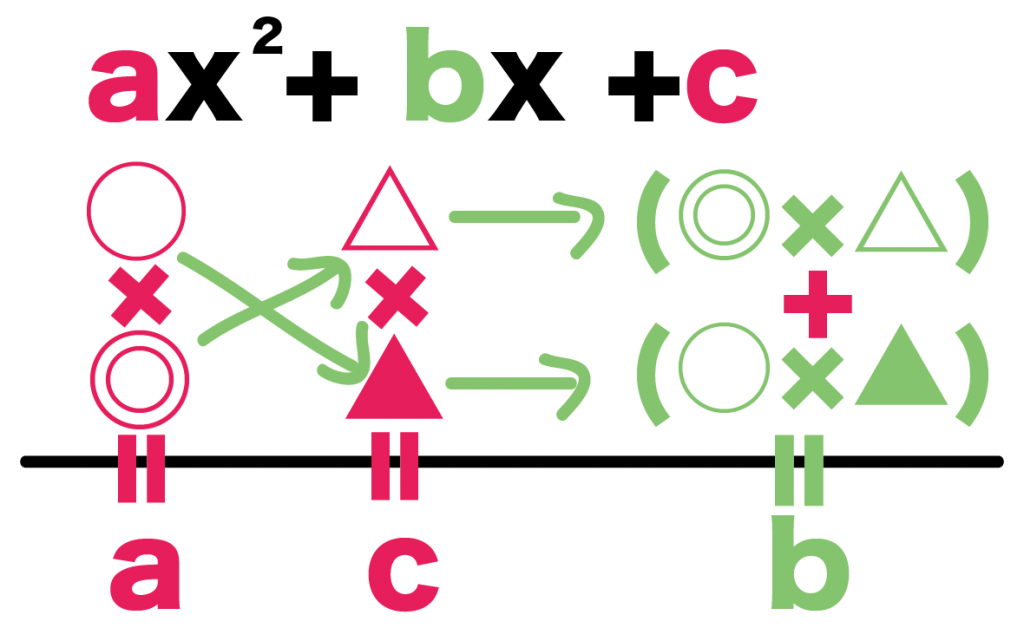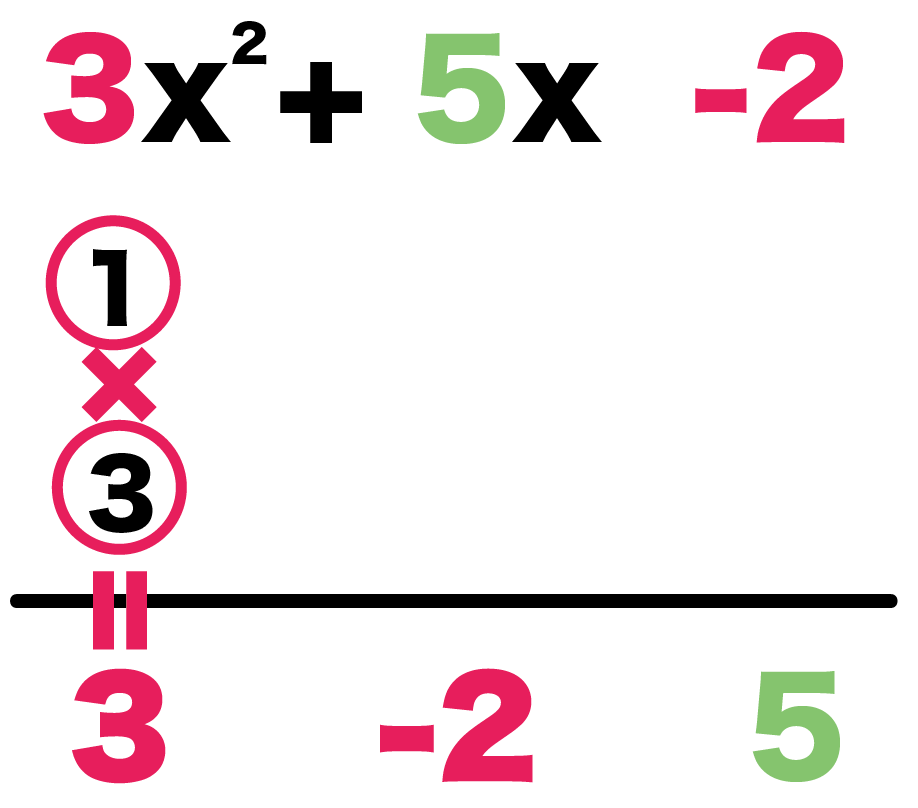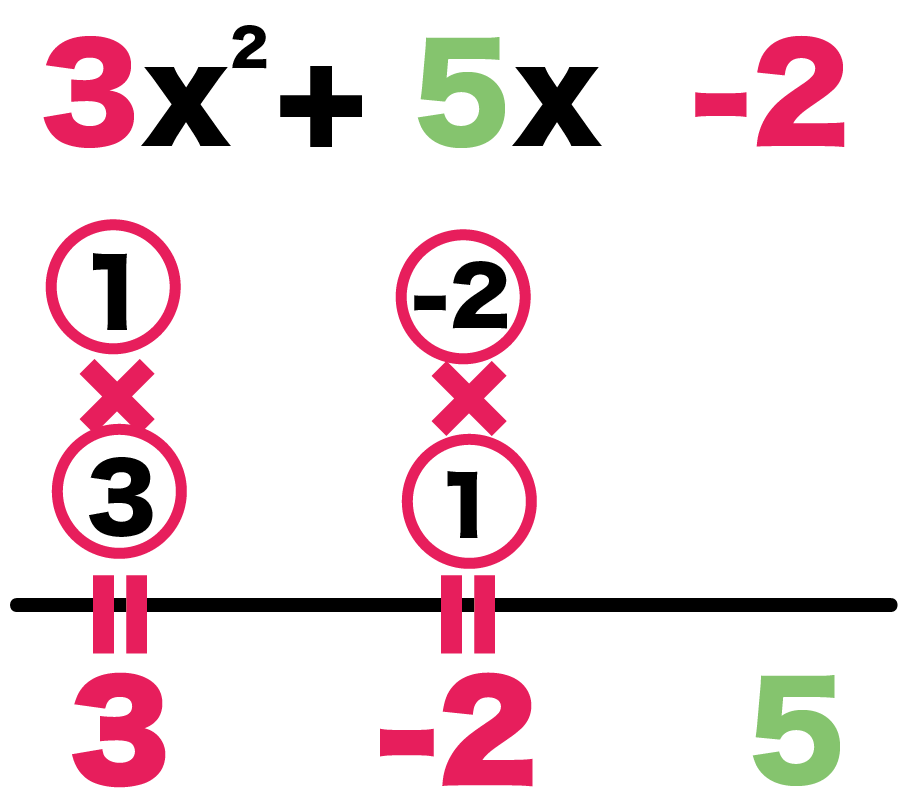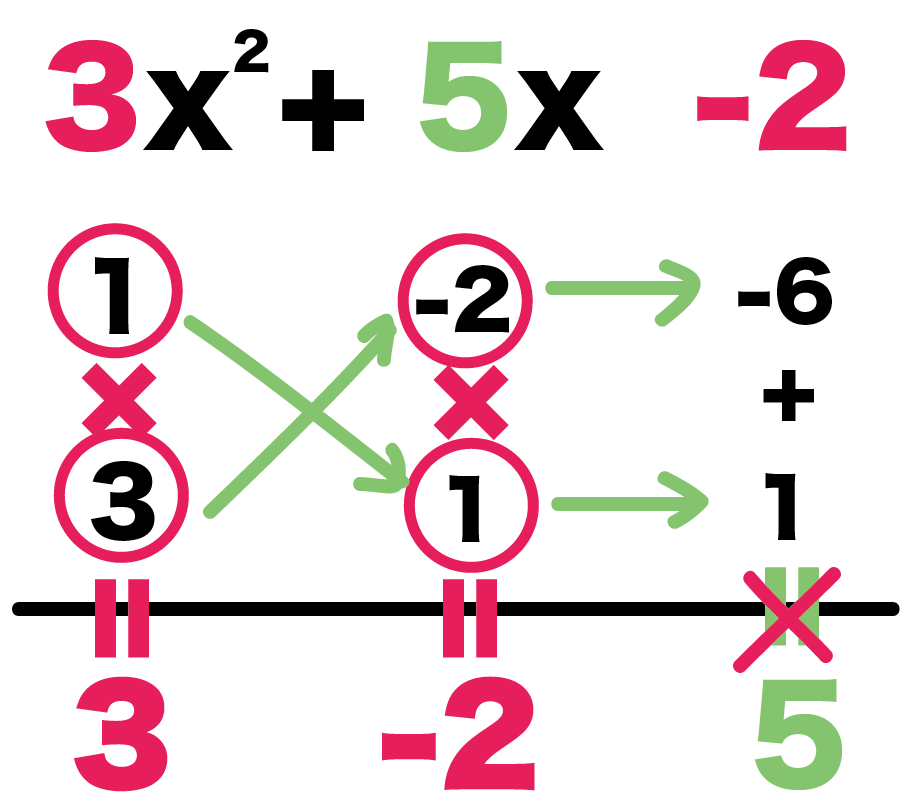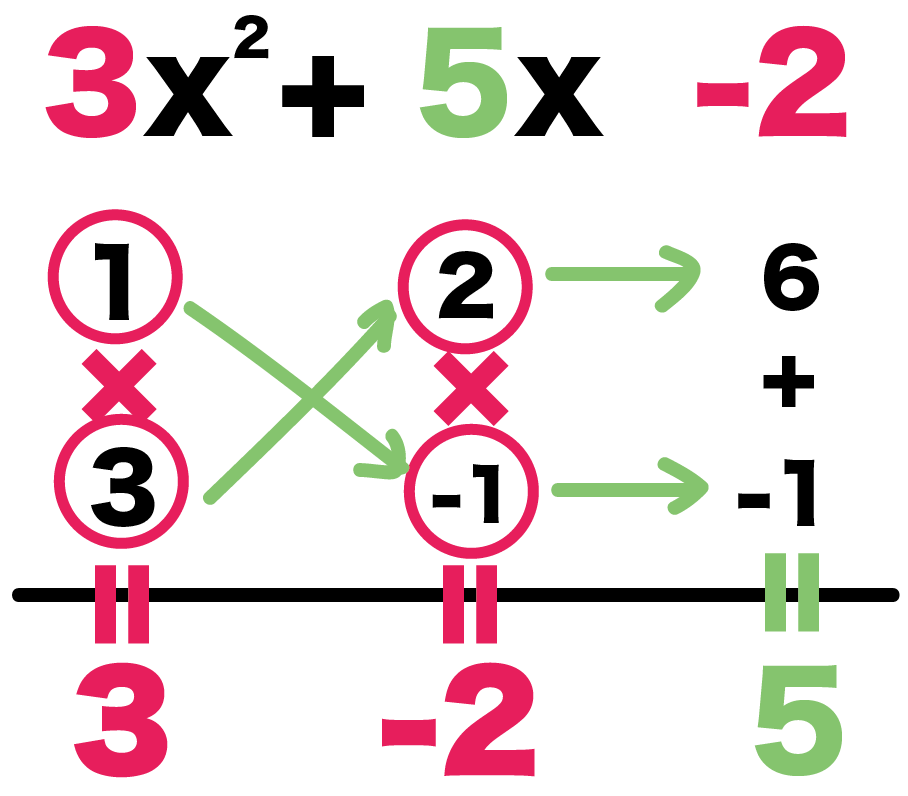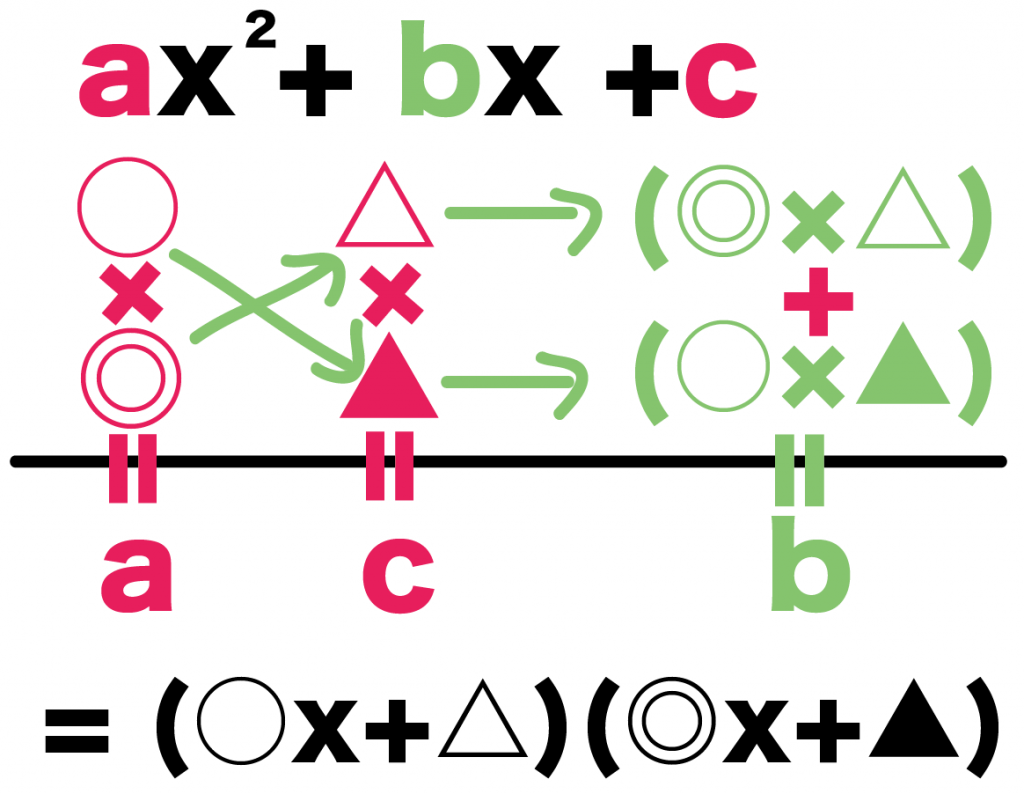【中学数学】たすき掛け因数分解のやり方がわかる5つのステップ
たすき掛けの因数分解のやり方がわからない??
こんにちは!この記事をかいているKenだよ。紅茶は午後にかぎるね。
因数分解にはいろいろな問題があるよね。
ときどき、ぜんぜん解けなくて泣きたくなるときも、ある。
よくあるのが、
因数分解の公式が使えない
とか、
共通因数でくくれない
って問題だと思うんだ。
そんなときに助けてくれるのが、
たすき掛けの因数分解
だ。
たすき(襷)といえば、
駅伝とか、
宴会の余興をイメージしちゃうかもね。
だけど、因数分解にもじつは、
たすき掛けという解き方があるんだ。
今日は、この解き方を5ステップで解説していくよ。
よかったら参考にしてみてね。
たすき掛けの因数分解のやり方がわかる5つのステップ
さっきもいったけど、
たすき掛けはつぎのときに役立つよ。
- 因数分解の公式が使えないとき
- 共通因数でくくれないとき
たとえば、つぎの例題みたいにね。
つぎの式を因数分解しなさい。
3x² + 5x -2

なぜなら、
公式は使えなさそうだし、
共通の因数もぜんぜんみつからないからね。
まさに、たすき掛けの因数分解にはもってこいの問題だ。
今日はこの例題をいっしょにといてみよう!
Step1. 線をかく
まずは、まっすぐな線をかいてみて。
定規は使わなくて大丈夫。
フリーハンドでいいから、すーっと直線をかいてみてね。
これが第1ステップ!
Step2. 係数をならべる
つぎは、直線の下に係数をならべよう。
かりに、
ax² + bx +c
を因数分解するなら、
a、c、b
の順番に係数をならべてあげるんだ。
つまり、
- xの二乗の係数
- 定数
- xの係数
ってかんじで左から順番にね。
例題の、
3x² + 5x -2
でもおなじさ。
直線の下に、左から、
- 3
- -2
- 5
の順番に係数をかけばいいんだ。
真ん中のxの係数がトリッキーな動きをするから、
順番を間違えないようにね。
Step3. かけ算のパターンを考える!
つぎは、かけ算のパターンを考えてみよう。
左2つの係数の、
- x2乗の係数
- 定数の係数
になる組み合わせをみつければいいんだ。
たとえば、
ax² + bx +c
だったら、
- かけたらaになる2つの数字
- かけたらcになる2つの数字
をさがせばいいんだよ。
例題でいうと、
- かけて3
- かけて-2
の組み合わせだね。
かけて3になるのは、
- 1×3
- -1×(-3)
の2つかな。
かけて-2になるのは、
- -1×2
- 1×(-2)
の2パターンだね。
これで第2ステップ終了!
Step4. たすき掛けになる組み合わせをえらぶ
さっきの数字の組み合わせの中から、
たすき掛けの計算にはまるもの
をえらぼう!
えっ。たすき掛けの計算とか知らないって??
たすき掛けの計算とはずばり、
斜めの数字同士をかけたやつらをたすと、右下の数になる
ってやつなんだ。
たとえば、
ax² + bx +c
だったら、
- ○×◎=a
- △×▲=c
- (○×▲)+(◎×△)=b
になるような、○・◎・△・▲の組み合わせをみつければいいんだ。
言葉では説明しずらいから例題をみてみよう。
これは力技だ。
当てはまりそうな数をいれて、たすき掛けを試してみよう。
かけたら3になる組み合わせとして、
- 3
- 1
の2つをぶちこんでみる。
つぎはかけたら-2になる組み合わせだ。
- -2
- 1
のペアーなんてどうだろう??
この4つの数字でたすき掛けしてみると、
- 3×(-2) = -6
- 1×1 = 1
になる。こいつらをたすと、
-6 + 1 = -5
になるね。
こ、こいつはxの係数の5じゃない!
この組み合わせじゃダメだ!!
じゃあさ、
-2と1の符号を入れ替えたらどうよ??
-1 と2って感じでさ。
そうすると・・・
- 3×2 = 6
- 1×(-1) = -1
になるね。
で、たしてみると、
6 -1 = 5
っておおお!
たすき掛け成立しちゃってんじゃん??
これだ!この組み合わせだ!!
・・・・・・・・
・・・・・・・・
っていうかんじで、
因数を変更してみたり、
符号を変えたりするんだ。
たすき掛けの因数分解になるまでねばってみよう。
Step5. 因数分解っぽくする
たすき掛けもいよいよ終盤。
たすきがけの組み合わせがわかったら、
因数分解っぽい形にしてみよう。
たすき掛けで書き出した数字のうち、
いちばん左のやつがxの係数、
真ん中のやつが定数(数字だけの項)になるんだ。
ax² + bx +c
の例だったら、
(○x+△)(◎x+▲)
になるんだ。
例題では、
- 1と3
- 2と-1
の組み合わせだったね??
よって、
xの係数は、
- 1
- 3
で、定数の項は、
- 2
- -1
になるんだ。
つまり、
3x² + 5x -2
= (x+2)(3x-1)
になるってわけさ。
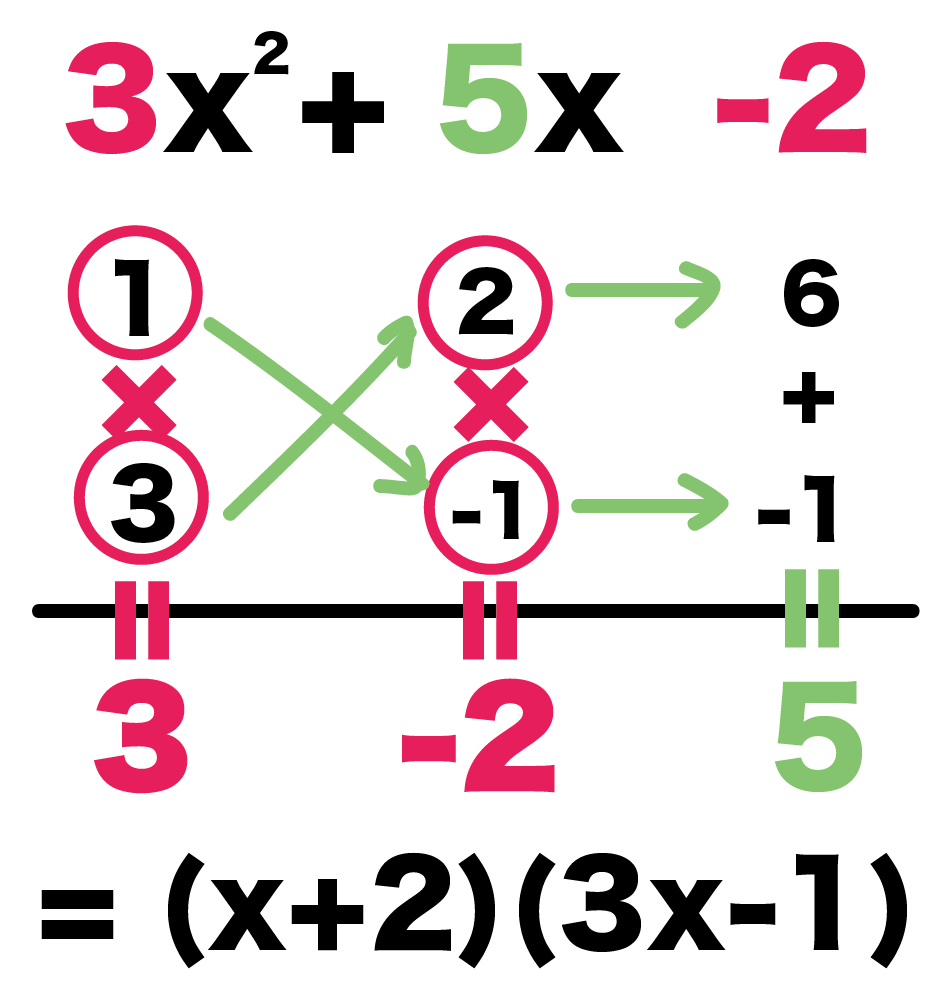
おめでとう!
これでたすき掛けもマスターだね。
まとめ:たすき掛けの因数分解は気合と根性で乗り切れ!
たすき掛けの因数分解はぶっちゃけむずい。
説明するのも苦しかったよ。うん。
だけど、解き方をおぼえちゃえばもうね、無敵。
必殺ワザをおぼえるものだと思って、
たすき掛けをマスターしちゃおう。
そんじゃねー
Ken