【簡単作図】相似の中心を使って拡大図をかく5つのステップ

相似の中心を使って拡大図をかいてみたい！

こんにちは！この記事を書いてるKenだよ。ビタミンEが欲しいね。

図形の相似を勉強していると、

相似の中心

という言葉が出てくるよね？？

相似って言葉でもちょっと怪しいのに、それの中心？？

ちょっとね、正直わけがわからない。

そこで今日は、相似の中心を使って拡大図をかく方法をわかりやすく解説してみたよ。

よかったら参考にしてみてね。

相似の中心を使って拡大図をかく5つのステップ

つぎの5つのステップで拡大図がかけちゃうんだ。

相似の中心を決める
相似の中心と頂点を結ぶ
ある頂点と相似の中心の距離を測る
倍率分だけ線分を伸ばす
新しい頂点を結ぶ

試しに、つぎの△ABCの2倍の拡大図をかいてみようか。

Step1. 相似の中心を決める

まず相似の中心を決めよう。

問題ですでに相似の中心がかかれているときは飛ばしてもいいよ。

△ABCではまだ相似の中心がなかったよね？？

だから、適当にポチッと点を打ってあげてね。

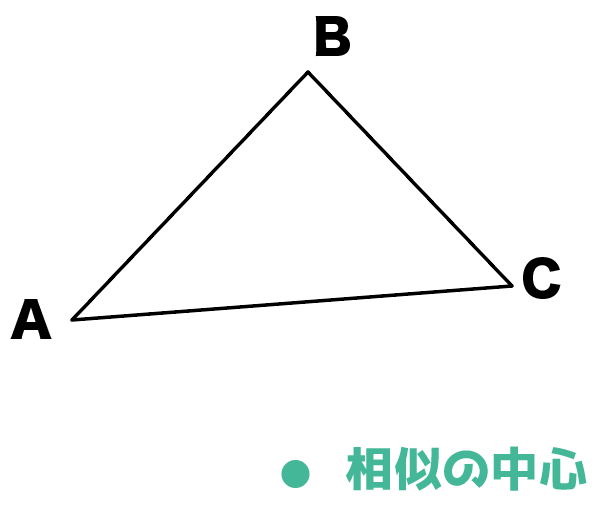
これが第一ステップ。

Step2. 相似の中心と頂点を結ぶ

つぎは、「図形の頂点」と「相似の中心」を直線で結んでみよう。

相似の中心をOとすると、

の線分を引けばいいってことね。

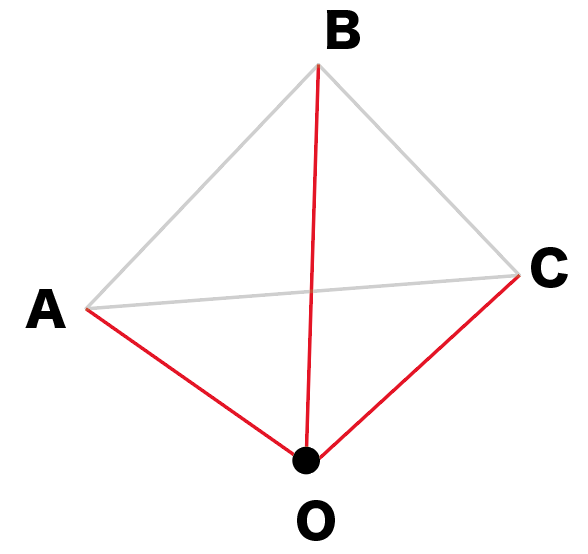
点を結ぶだけだから楽勝だぜ。

Step3. 相似の中心と頂点の距離を測る

「相似の中心」と「頂点までの距離」を測ってみよう。

さっきかいた線分の長さを測るだけ！

定規でさっきの線分の長さを測ってみると、

OA = 2 cm
OB = 4 cm
OC = 3 cm

になった！！

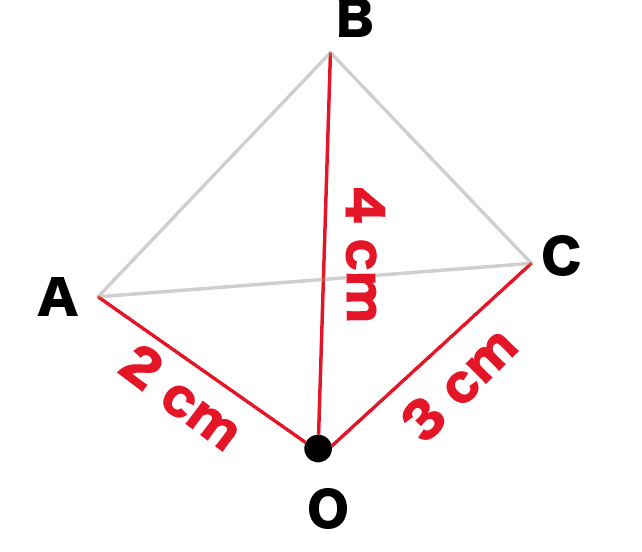
えっ。都合が良すぎるって？！

これはしょうがない。

定規で測ったらこうなったんだもん。

Step4. 倍率の分だけ線分を伸ばす

つぎは「倍率の分だけ」線分を伸ばしてみよう。

3倍の拡大図なら3倍、

100倍の拡大図なら100倍に伸ばしてみればいいんだ。

△ABCでは2倍の拡大図をかきたかったから、

をそれぞれ2倍に伸ばしてみよっか。

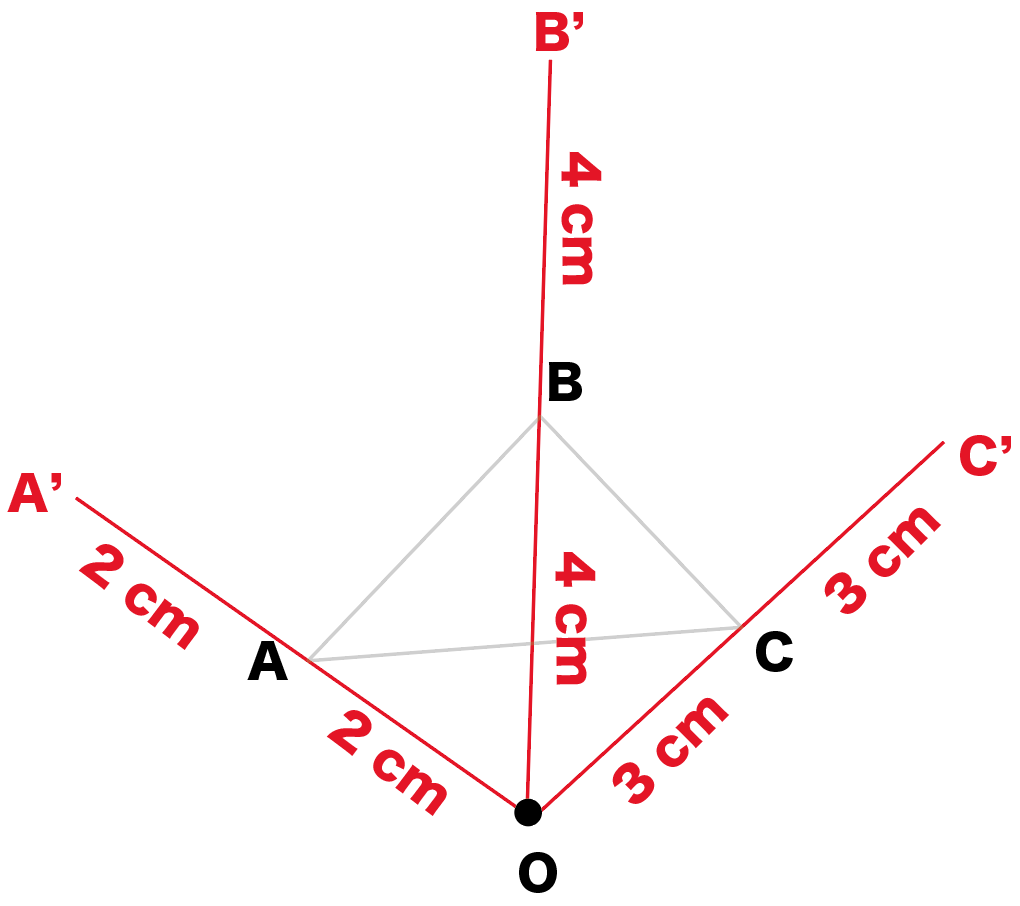
伸ばした線分の先っちょをそれぞれ、

A’
B’
C’

とするよ。

Step5. 新しい頂点を結ぶ

最後に、新しくできた頂点を結んでみよう。

結んでできた図形が拡大図だよ。

△ABCの例でいうと、

A’
B’
C’

を結んでやればいいね。

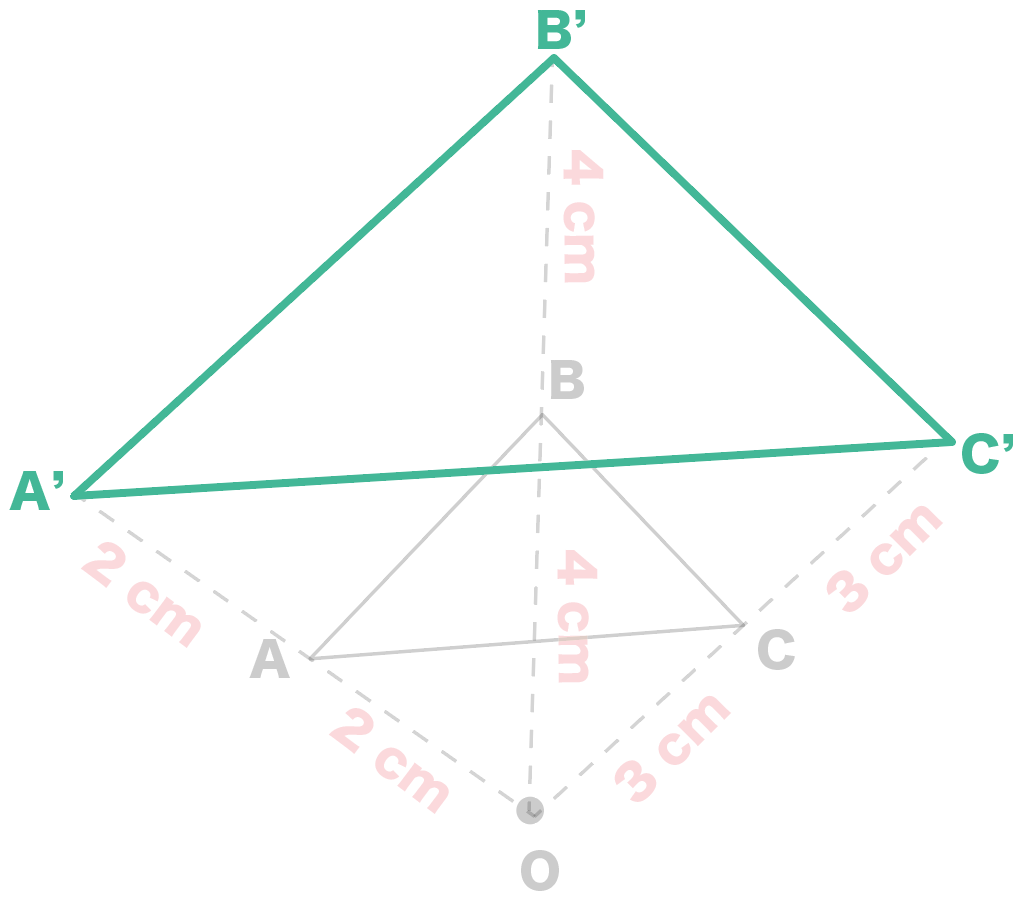
新しくできた△A’B’C’が△ ABCの2倍の拡大図だ！

なぜ、相似の中心を使うと拡大図がかけちゃったのか？

こんな感じで、

「相似の中心」から「各頂点までの距離」の比が等しいとき、

2つの図形は、

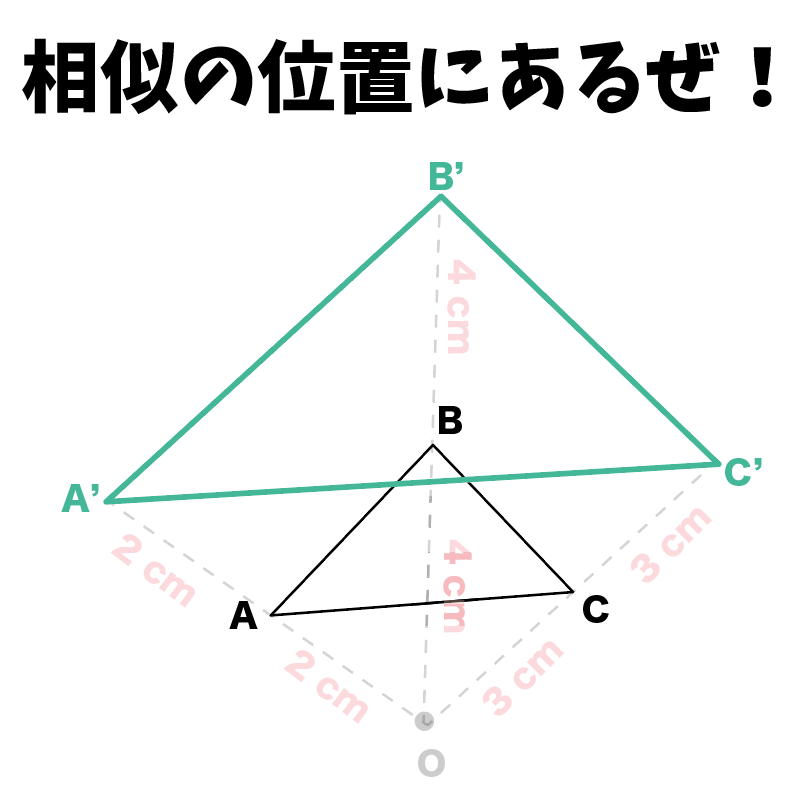
相似の位置にある

っていうんだ。

んで、相似の位置にある図形たちは相似になっているよ。

今回の例でいうと、

△ABCと△ A’B’C’は相似の位置にある

って言えるわけね。

なぜなら、

OA : OA’ = 1 :2
OB : OB’ = 1 : 2
OC : OC’ = 1 : 2

になっていて、相似の中心Oから各頂点までの距離の比が等しくなってるからね。

でもなぜ、相似の位置にある図形同士が相似なんだろうね？？

その理由は、

平行線と線分の比を使うとわかるよ。

さっきの例でいうと、△OA’B’と△OABに注目してみて。

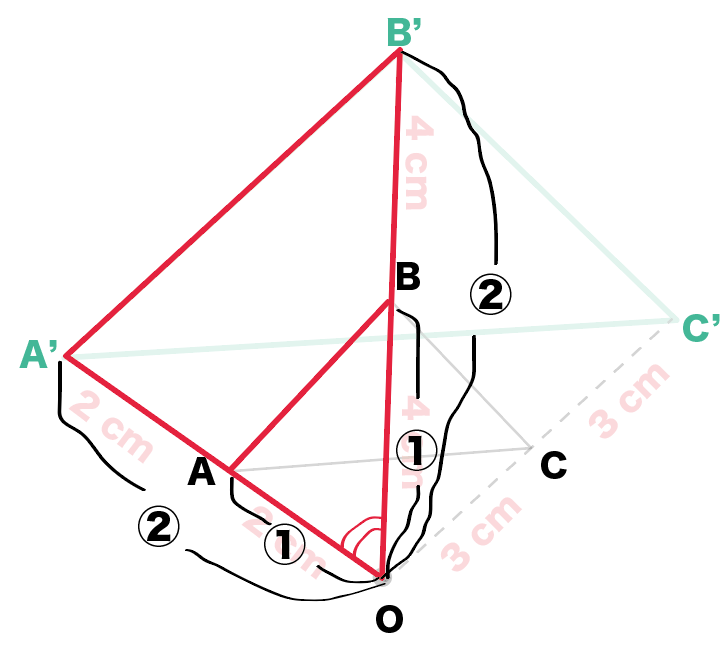
OA: OA’ = OB : OB’ = 1 :2

になってるよね？？

しかも、

∠AOBは共通。

「2組の辺の比とその間の角がそれぞれ等しい」っていう相似条件が使えるから、

この2つの三角形は相似になってるわけだ。

対応する辺の比が等しいはずだから、

AB : A’B’ = 1 :2

になるね。

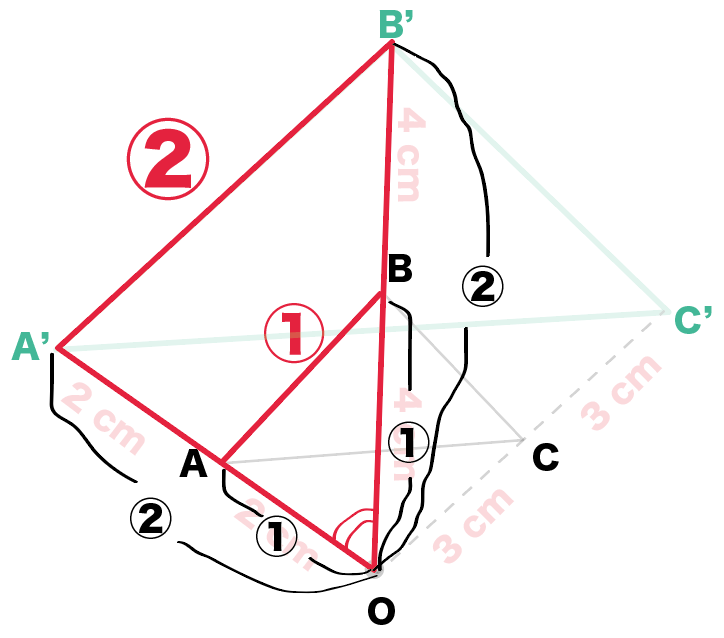
こんな感じで他の辺に対しても同じようにやってみると、

BC : B’C’ = 1 : 2
AC : A’C’ = 1 : 2

になってるんだ。

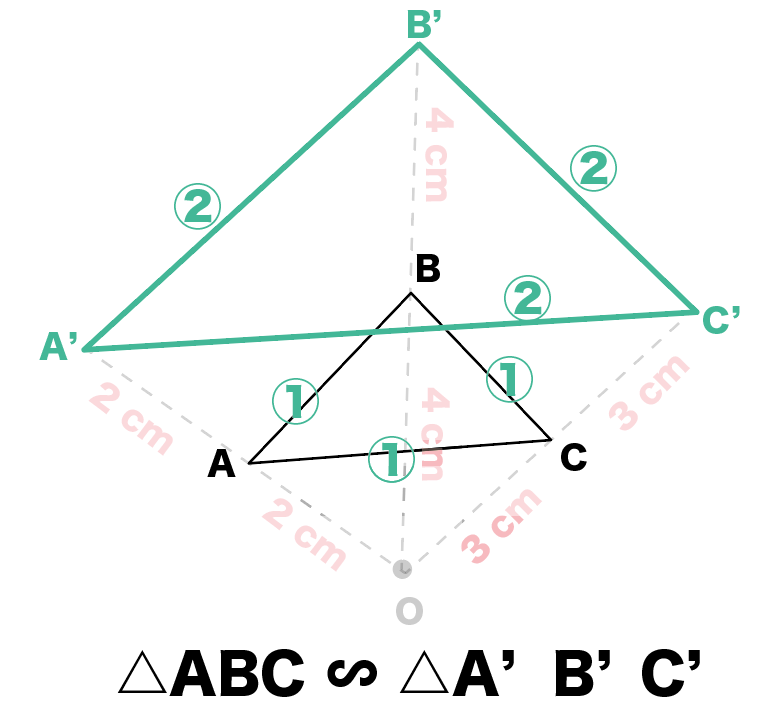
よって、△ ABCと△ A’B’C’の3組の辺の比が1:2でそれぞれ等しいから、

△ ABC∼△ A’B’C’

が言えるんだ。

どう？ちょっとスッキリしたかな？

まとめ：相似の中心を使って拡大図をかきまくろう！

相似の中心を使ってしまえば、拡大図のかきかたも簡単。

相似の中心を決める
相似の中心と頂点を結ぶ
ある頂点と相似の中心の距離を測る
倍率分だけ線分を伸ばす
新しい頂点を結ぶ

の5ステップでいいんだ。

相似の中心を使いまくるのもいいけど、

なぜ、相似の中心を使えば拡大図がかけるのか？

ってこともおさえておいてね。

そんじゃねー

Ken