中学1年生の数学単元で「一次式」と「二次式」という言葉が登場します。
一次式とか二次式とか聞こえはかっこいい。ガンダムのパイロットが使ってそうな数学用語ですよね？？ 「こちら、司令室。一次式、二次式、ともに完了。ラジャー」みたいな感じで。
ところが、です。
ぶっちゃけ、ぶっちゃけ、です。
中学1年の数学で「一次式」について勉強したけどよくわからない！一次式の説明文を何度読み返してもわからない！！どうしよう！
困ったので数学の教科書を読んでみると、
項
のように、文字が1つだけの項を1次の項といいます。また、1次の項だけの式、または、1次の項と数の項の和で表される式を一次式といいます。
という説明が書いてあります。
塾で予習していた中学生ならばこの問題に即答できるかもしれません。
ただ、数学の授業ではじめて「一次式」を勉強する方にはよくわかりませんよね？？ 一次式を理解できなければ二次式もわからずにゲームオーバーになってしまいます。
そこで今日は、
次数の意味から5分でわかる！一次式と二次式の違い
という記事を書いてみました。一次式と二次式の違いにピンと来ていない中学生の方！よかったら参考にしてみてください。
以下が記事のもくじです。
それではさっそく確認してみましょう。
一次式と二次式の違いを理解するために必要なこと。それは、
次数とは何か？！？
を知っておくことです。「次数」の意味がわからないと、一次式や二次式の違いがスッキリしません。っということで、まずは次数の意味を確認していきましょう。
次数とは、
項に文字が掛けられている数
を意味します。たとえば、
2つ目の項である「-b」はどうなるでしょう？？ これは
掛けられた文字の数は「1つ」ですよね？？ つまり、この項の次数は一次となります。
同様に、最後の項「9」をみていきましょう。この項には数字しかありません。どこをどう探しても文字が見当たりませんね？？ こういう場合の次数は「0」になります。文字がない数字だけの項の次数は「0」になることを頭にいれておきましょう。
さて、一次式と二次式の基礎である「次数」の解説は終了しました。次数を理解しちゃえば一次式も二次式もひとひねり。
超ラクショーです。
一次式とは「一番大きい次数が一次である文字式」のことです。ここでは「一番大きい」ということに注目してください。次数の合計ではなく最大の次数に注目することがポイント。
たとえば先ほどの文字式にちょっと似ている
すると、
けっして、
という間違えをしないようにしましょう。
一次式を理解しちゃえば二次式もわかったようなもんです。
二次式とは「一番大きい次数が二次である文字式」のこと。一次式との違いは「一番大きい次数が二次」という箇所だけです。
一番最初に例としてあげた
3つの項の中で一番大きい次数を持つのは
以上で一次式と二次式の見分け方の解説は終了です。
一次式と二次式を見分ける際にもっとも重要なのは、
文字式で一番大きい次数を持つ項をさがす
という作業です。これが瞬時にできるなら大丈夫。一次式だろうが二次式だろうが三次式だろうが見分けることができます。
それでは、また今度です。
Ken
中学数学で文字式を勉強していると、
「項と係数」
という新しい数学用語が登場します。これはいったい何ものなのでしょうか？？
項と係数の違いを確認して数学のテストでいい点数をとっちゃいましょう。
この「項と係数」という新しい数学用語の理解を深めるため、まずは文字式に注目しちゃいましょう。
文字式とは以下の3つの要素でなりたっています。
文字式にふくまれる要素のうち、
+に挟まれた数字や文字
を「項」といいます。
たとえば、
2-8+7
という式があったとしましょう。
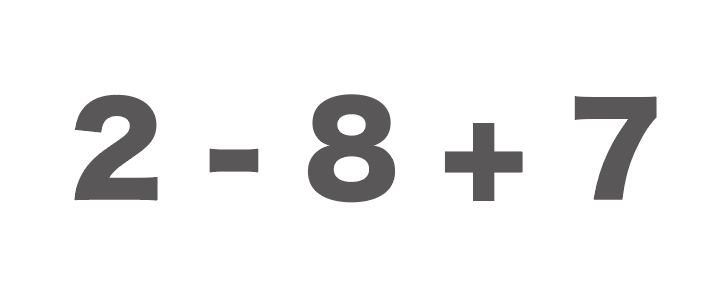
これをいったん、＋だけの式に直すと、
2+(-8)+7
になりますね？ 「＋に挟まれた数字や文字」が項なのでこの場合だと、
が項になります。
「項」についてもっと理解を深めたい！
という方は「項の意味を100%理解できる方法」という記事を読んでみてくださいね。
さて、項の正体はわかりましたね？？
それでは次に「係数とは何か」を確認していきましょう。
係数とはカンタンにいってしまえば、
文字の前についている数字のこと
です。さっきの文字式から2aという項を例にとりましょう。
文字式における1つの項は、
の2つの要素で成り立っています。文字式の文字についている数字が「係数」なわけです。見た目からも係数の意味からもわかりやすいですよね？？
ふう！項と係数は楽勝でしたね！？
それでは、また今度です＾＾
・・・・・・・
といいたいところですが、項と係数には2つだけ注意する点があるのです。これを最後に確認してみてください。
文字式の項において、文字の前に数字がないとき。たとえば、
この場合、文字の前に数字がないのでaとbの項の係数は「0」ではないかと疑ってしまいます。ふつうに考えたらこうなります。
じつは、文字の前に数字がない項の係数は「1」なんです。
これをしっかりと覚えてください。文字式の表し方のルールで確認したとおり、
文字に1がかかっている場合は1を省略しましたよね？？
そのため、係数がゼロのようにみえてもきちんと「1」が係数としてかかっているのです。
見えない「1」という係数に注意しましょう。
分数の係数にも注意が必要です。
とくに分子に文字、分母に数字という文字式がけっこうやっかいなんです。
たとえば、
xの係数を求めて？？
と言われたら何て答えます？？
これまでの係数に忠実にしたがえば、
xの前に数字がついてないから係数は1じゃないの？！？
という答えが飛び出してきそうです。だがしかし、この答案はとんでもなく間違っています。
間違えを防ぐためにも、
分数を含む項では、分子から文字をいったんおろして考えてください。
先ほどの
としてやります。すると、
となります。よーーく見てみると
つまり、
それでは、また今度です。
Ken
中学1年数学で勉強する「式の値」の解き方がよくわからない。
そんな声をよく耳にします。式の値とか急に言われてもピンと来ないし、いくら想像してもいったいどんなモンスターなのか検討もつきません。
できれば「式の値」という中1数学の単元をスキップしたいですよね？？難しい数学の単元なんてお断りしたいです。
だがしかし、です。
「式の値の解き方」を知らずに中間・期末テストを迎えるとテストで確実に爆死します。
中学数学でいい成績をとっておきたい。
そんな目標を持っていたら「式の値の解き方」をマスターしておきましょう。この記事では以下の順番で式の値を解説していきます。
式の値の解き方を勉強すれば、中間テストの数学でいい点数をとれること間違いなしです！！
それでは、さっそく見て行きますよー
式の値とはいったいどこの何者でしょうか？？？
名前を見る限りむずかしくて気難しいヤツにみえます。だがしかし、中1で勉強する式の値はいたってシンプルな内容なんです。
式の値とはずばり、
文字式の文字に数字を当てはめたときの値
のことです。
「文字式の文字に数字を当てはめたときの値」=「式の値」
というわけですね？？ なるほど、ただの省略形だったわけですね。
中学の数学では「文字に数字を当てはめる」作業のことを「代入」、当てはめる数のことを「文字の値」と呼んでいます。
式の値の具体例をみていきましょう。たとえば、次のような文字式
があったとしましょう。これはある中学生のひと月のお小遣いの状態を表しています。xという文字は「洗った皿の枚数」です。つまり、1枚お皿を洗うという家事の手伝いをすると40円お小遣いが増えるというわけです。
今月は皿洗いに力を注いだので43枚の皿を洗う事に成功しました。すると、この中学生の今月のお小遣いは、
と計算できますよね？？
このときの「文字mに43を入れること」を「代入する」といい、文字式に代入する「43」を「文字の値」と呼んでいるんです。
それで、文字式にある数字（文字の値）を代入して求めることができた値を「式の値」と呼んでいます。
上の例でいえば、m（皿を洗った枚数）に43を代入した結果得られる「2220」がこの文字式の「式の値」というわけです。もうおわかりですね？？
まとめると、
式の値とは、文字式に数字をぶちこんだときの計算結果
ということになります。
式の計算は思ったよりカンタンでしたね？？？
文字式の文字に数字をぶちこんでやるだけです。その結果得られる数字を「式の値」と呼んでいるわけです。
ただ、「式の値」の問題の解き方にはある1つのコツがあります。
それは、
あせらずにゆっくり式の値を求める
ということです。ものすごく当たり前のこといっていますね。 ただ、式の値を求める計算問題では焦るとミスしてしまうことがあるのです。
したがって、
式の値の問題では計算過程をはぶかずにすべて書くことをおすすめします。
なぜなら、マイナスの符号が絡んだ「式の値の計算」ではミスが出やすいからです。
たとえば、
のとき、次の式の値を5秒で求めなさい
という式の値の問題があったとしましょう。このとき、
式の値？？ はあ？カンタンだよ、文字に数字を入れるだけやろ？！
といきり立っていきなり答えを書き込んではいけません。計算ミスを防ぐために文字に数字を代入する計算過程を丁寧に書いてみましょう。
先の例で言えば、
という感じで式の値を算出する計算過程を書いておく。これにより−の符号関連の計算ミスを最小限にとどめることができます。
計算過程を書くなんて正直だるいですよね？？
ただ、数学のテストでケアレスミスをなくすために途中の計算式を書いた方がいいんです。決して答えを急いではいけません。
ゆっくりと慎重に式の値を計算する。
これが唯一の式の値の解き方のコツです。テスト時間に余裕がある限りなるべくゆっくり計算問題をといてみてください。
式の値の解き方はいかがだったでしょうか？？
「式の値」とか名前はクールですがあまり大したことありまえせんでしたね？？。
式の値の計算問題でいつもミスをする！そもそも式の値の意味がわからない！！
そんな中学生の助けになったら嬉しいです。
それでは、また今度です！
Ken Sawai
中学1年生の数学をおそるおそる勉強していくと、
などなどの英文字を使った「文字式」を勉強し始めます。
アルファベットをガンガン使っていくので雰囲気はかっこいいです。文字式を黒板に書いてみる？？ それだけで世界の科学者になった気分すらなれます。数学を勉強した甲斐がありましたね。？？
しかし、しかしです。
文字式の表し方には覚えなければいけないルールがあります。
ルールですので理由なんかありません。昔々の数学者たちが勝手に決めてきたのものです。
数学を勉強するためには覚えなければいけないのです。
今日は文字式を勉強したての中学生の方々に、
文字式の表し方で注意したい7つのこと
を紹介します。「文字の式」の単元に突入した？？？？ まずは文字式の表し方のルール・注意点を確認しちゃいましょう。
中1の文字式の勉強が楽しくなる！！
「文字式の表し方」に関するそんなお得な注意点を7つにしぼって紹介していきます。
文字式では掛け算記号「×」を省きます。
無視します。
存在しなかったことにします。
いままでの数学では掛け算記号を省くなんて考えられませんでした。
たとえば、文字aと文字bを掛けた計算式を考えましょう。今までなら、
と書くのが普通でした。しかし、正しい文字式の表し方では、
と書き直すことができます。みごとに掛け算記号×を無視していますよね。 ×記号があった元の場所さえもなかったことにしています。
先ほど「直すことができます」と言いましたが、
文字式のテストで100点をとるには掛け算記号を省かねばなりません。
掛け算記号×をはぶけるようになりましたね？？
次は英文字と数字を並べる順番を押さえちゃいましょう。どんな順番でも文字式の答えは一緒。だけれども、文字式の表し方というルールに従わないといと不正解になってしまいます。
文字式を並べる順番のルールはずばり、
数字→文字→アルファベット順
です。数字を先に書いて、その後に英文字をアルファベット順（a, b, c, d……y, z）に並び替えればいいわけですね。
たとえば、
になります。掛け算記号×を無視して正しい順番に並び替える。これが文字式の表し方の鉄則です。
文字式の表し方では「指数」を使うことが大切です。同じ文字を何度も掛けている文字式があったら「指数」を用いて省略してみましょう。たとえば、
という文字式があったとしましょう。このとき先ほどの2つのルールに従うと、
と表せますよね？？ 掛け算記号を無視して数字、アルファベット順に並べる。これだけです。
だがしかし、これだけでは○をもらえません。より正確な文字式の表し方に従うならば、
としないといけません。2回掛け合わされているbを指数を使って表現しているだけです。これならば長ったらしい文字式も指数で短くできますね。
文字式の表し方ではこれまで、
などたくさん数字や文字を書く手間を省いてきました。ここではさらに、
数字の「1」をはぶく
という文字式の表し方のルールが加わります。たとえば
としてはいけません。文字式の表し方では
文字式で「×」を省略してもいいことはわかりました。文字式の表し方を勉強していると当然、
割り算記号「÷」はどう文字式で表すのか？？？
という疑問が浮かんでくるでしょう。「÷」記号は「×」の兄弟のようなもの。当然、何か文字式の表し方のルールがあるはずです。
そう。そうです。あるんです。
正しい文字式の表し方は、
「÷」の代わりに「分数」をつかう
というものです。ちょっと言葉だけではわかりませんね？？ 実際の例題をみてみましょう。
たとえば
と表すことができます。つまり、÷記号の後ろの数字を分母にもってくればいいのですね。
文字式の表し方では、
「掛け算記号×」と「割り算記号÷」をはぶいていいよー
というルールがありましたね？？ この流れでは当然、
じゃあ、「足し算記号＋」と「引き算記号−」も省略していいの？？
という疑問が湧いてくるはずです。掛け算も足し算も似たようなもんですからね。
だがしかし、
文字式の表し方では、
ゼッタイに「＋」と「−」の計算記号を省略してはいけません。
これはゼッタイです。どんなに賄賂を贈ってもダメです。えっ、肩もんだってダメですよ。
実際に文字式の例をみてみましょう。たとえば、
という文字式があったとしましょう。掛け算と割り算の記号は省略できます。ただ、足し算引き算の記号はそのままにしておいてください。
すると上の文字式は、
となります。すべての計算記号を省略できない、ということを肝に命じておいてください。
最後に文字式の中の「英文字（アルファベット）」の選び方です。
文字式にはたくさんアルファベットが登場します。aやらbやらcやらxやら。なぜaを選ぶのか？ なぜxなのか？？ とういことが不思議でたまりませんよね？？
文字式の表し方では以下の2点だけ注意してればいいです。
まず、「文字であらわす数値に由来する英単語」があるのか注目してください。たとえば、「数字」を文字で表現するとしましょう。「数字」は英語でnumberです。英語の授業で習いましたね？？
そこで数字を表現する英文字には「n」が選ばれることが多いです。なぜなら、nはnumberという英単語の頭文字だからです。
それでは逆に由来の英文字がなかったらどうすればいいのでしょう？？
そのときはアルファベットの先頭か最後、つまりa, b, c, d, e….か、もしくはz, y ,x, w, ….などを使いましょう。
文字式のネタに困ったときはアルファベットの先頭か末尾
ということを覚えておけば問題なしです！
以上の7つが中1数学の文字式の表し方で注意することでした。ぜんぶで7つしかありません。
これらのルールを使ってさまざまな文字式で表していきましょう。
それでは、また今度です。
Ken
中学数学でもっとも頻繁に利用する計算法則。それは、
分配法則（distributive property）
というものです。「分配法則のチョー便利な1つの使い方」という記事でもお伝えしましたが、もう一度「分配法則」を復習してみましょう。分配法則とは次のような計算法則でした。
a, b, cという3つの数があったとすると、
分配法則のことをちまたでは「カッコをはずす法則」と呼んでいます。
()を含んだ複雑な計算式も分配法則を使えばイチコロ。1発か2発でカッコなしの計算式に直せるのです。
これは便利ですよね？？ 分配法則は3年間を通して頻繁に登場します。がっちり押さえておきましょう！
ところが、です。ところが。
なぜ分配法則は成立するのでしょうか？？
たしかに分配法則は超便利な計算法則。だがしかし、分配法則が使える理由を考えずに乱用していては数学が得意になりません。
たとえるなら、野球のルールを知らずにバットを振り回しているようなもんです。今日は、そんな便利な分配法則の証明をわかりやすく解説してみました。
分配法則がなぜ使えるのか証明したい！！
そんなアツい志をもった方に参考にしてほしいですね。
分配法則の証明をするため、さきほどの
でしたよね？？ 図で表すとつぎのようになります。
次は同じ英文字ごとに足し合わせてみましょう。aはa、bはbという感じです。この状態ではカッコの外に数字がかけられていないので()を自由に取り外せますね！
すると、aがc個、bもc個たし合わされていることに気づきます！だって、(a+b)のセットがもともとc個ありましたからね。ハンバーガーとポテトのセットが2つあったらハンバーガーが2個、ポテトも2個あるのと同じです。
最後にもう一度「掛け算」の意味を振り返ってみます。
掛け算とは、
ある同じ数のセットを繰り返し足し合わせたもの
でしたね？？ この掛け算の意味を考慮すれば、
「aをc個足し合わせた数」=
「bをc個足し合わせた数」=
と掛け算に書き直すことができるのです。
この3ステップを経てようやく、
といえるわけですね！分配法則が証明できてよかったよかった！
一番はじめに5分で分配法則を証明することを目標としていました。
さて実際、どうだったでしょうか？？？ ものの3分、いや35秒ぐらいで分配法則を証明できちゃいましたね。
中学数学の教科書には分配法則の証明はのっていません。
だがしかし、自分の頭をつかってみて、
なぜ分配法則がいえるのか？？
と考えて証明してみることが大切。数学を今後も勉強していく上で「なぜ？なぜ？？」という問いをしながらすすめてみてください。
それでは！また今度です。
Ken
中学1年生がでくわす最初の難関。
それは「文字の式」という数学単元です。小学校で勉強した算数とぜんぜん違いますよね？？その理由としては、
英語の文字（a, b, c, d…）を使った計算式がばんばん登場するから
でしょう。数字の代わりに文字式を使う。文字式に実際の数字を入れてみる。
中学1年の文字式の単元ではそんな技が必要になってきます。
これって、文字式のあつかいに馴れていない中学1年生にとって大変なことですよね？！？おそらく中学1年数学の「文字式」で一番多くの脱落者がでるでしょう。
そこで今日は、
なぜ中学1年生の数学で「文字式」を勉強しなければいけないのか？？
ということを徹底的に解説してみました。 おじさんになってみて気づいた文字式を勉強すると便利な理由を2つほど紹介します。
文字式なんてクソくらえ！ 数学なんかやめていぇる！
とやけくそになっている方。とりあえずこの文字式の記事を読んでみてくださいね。
文字式を中学1年から勉強して何かいいことあるのか？！？
そんな疑問にお答えします。ぼくは文字式を勉強すると以下の2つのハッピーなことが起こると信じています。
文字式を勉強すると「未来を予測できる」ようになります。 文字式は占いでも超能力でもありません。水晶玉でもありません。
文字式は日常生活でおこる出来事を「英文字」と「数字」だけで表現できちゃう道具です。文字と数字だけで未来を予測できるんです。
えっ。どういうことかぜんぜん分からないですって！？？具体的な例で確認していきましょう。
ある日、サンタクロースがいたとしましょう。今年のプレゼントを苦悩しながらも決定。男の子には「ガンダムの消しゴム（100円）」。女の子には「プリキュアの化粧セット（12980円）」を上げることにしました。プレゼントの内容を決めた時点ではこのサンタが担当する男女の人数はわかっていません。
そこで、サンタはプレゼントにかかる総費用を文字式で表してみました。プレゼントをあげる男の子の人数をa人、女の子の人数をb人とします。すると総費用は、
となります。この文字式のa、bの値に数字を当てはめると、サンタが負担する費用を計算できるのです。つまり、どれぐらい費用がかかるのか、という未来を予測できることになります。
たとえば、男の子が10人、女の子が8人。プレゼント配達の担当になった場合を予想しましょう。aに10、bに8をいれてやれば、
と。こんなに少人数なのに・・・・・サンタの2015年クリスマスの負担額は10万円を超えることを予想できます。 財布の中に5万円しかなかったサンタは、いそいでアルバイトの面接に複数応募したとさ・・・
文字式をうまく使ってやれば謎をとけるようになります。
うぶな中学1年生はまだ謎をといた経験があまりないはず。あっ、名探偵コナンは例外ですけどね。
文字式を利用してやると、次の単元で勉強する「方程式」をばんばん作れるようになります。この方程式とはいわば「謎をとくための道具」なのです。
たとえば、先ほどのサンタを例にとりましょう。彼はクリスマスの司令部から次のような通知をうけとりました。
女の子の人数は4人だけど男子はまだわからないね
と。サンタの持ち金は10万円。男の子には100円のガンダム消しゴム、女の子には12980円のプリキュアセットを買うと固く決めていました。それじゃあ、男の子は最大何人まで担当することができるのでしょうか？？？
こんな謎があったとしましょう。
これは方程式という謎解きマシーンを利用すれば一発で算出できちゃいます。この状況を文字式で表現してやりましょう。サンタが担当する男の子の人数を
と文字式で表現できます。この文字式と等式が組合わさった計算式を「方程式」と呼んでいます。これをといてやると、
という答えがでます。つまり、男の子は最大480人までプレゼントをあげられるわけです。
これが文字式を利用した方程式の例です。
ほら？？ 文字式を使えば謎がとけましたでしょ？？？
中1の数学から文字式を勉強するとこんないいことがあるんです。
文字式の使い方を覚えておけば、もしサンタになっても安心ですね。プレゼントにかかる経費を予想したり、プレゼントを配る人数を算出することができます。
文字式は日常生活にもっとも密接に結びついた単元
と言っても過言ではありませんね。
それでは、また今度です。
Ken
中学1年生の「正の数・負の数」の単元に、
という意味のわからない数学用語が2つ登場します。数学を勉強したての中学1年生にとって、
はあア？整数の集合？？え？どこのゲーセンに集合するんだって？？
自然数の集合？？ あ、おれの地元は自然の集合だからね、なんちゃって
という感じで「整数の集合」や「自然数の集合」の意味がわからなすぎて数学が嫌いになってしまいそうです。これでは日本の数学勉強人口がぐんぐん減ってしまいます。これはいけすかない！
そこで今日は「整数の集合」と「自然数の集合」という数学用語を理解できる記事を書いてみました。その名も、
3分でわかる！「整数の集合」と「自然数の集合」の違い
数学が好きでない中学生の方でも3分でわかるように書いてみました。「正の数・負の数」の単元でつまづきそうになった中学生の方は参考にしてみてください。
「整数の集合」と「自然数の集合の違い」を確認する前に、
集合とは何者か？！？
ということを解説しましょう。
オンライン大百科Wikipediaで「集合（set）」の意味を調べてみると、
「もの」からなる「集まり」である
とあります。ものの集まり？？ なんじゃそりゃ！ってなりますよね。
ぼくは個人的に「集合」の意味をつぎのように捉えています。
集合とはグループのようなもの
です。えっ。Wikipediaよりわかりづらいですって？！？ そうですね、理解をふかめるために具体例をだしてみます。
たとえば、「自分」という1人の人間を考えてみてください。ぼくは日本人で埼玉県に住んでいるおにいさんです。この「ぼく」という人間は以下の3つのグループ（集合）に属していることがわかります。
これらが集合の良い例です。
つまり、集合に属する「もの」は集合内で似たような性質を持っているのです。
先の「日本人」という集合では「日本に住んでいる、もしくは生まれ育った人間」だけが「日本人」という集合に属することができるのです。なんか人種問題に発展しそうなのでここら辺に言及をとどめておきましょう。
集合には大小関係があります。小さい集合もあれば巨大な集合もあるというわけです。
それじゃあ、
という3つの集合で一番大きなものはどれでしょうか？？ こ、答えは、CMのあとで・・・・・
＜＜CM＞＞
答えは、
人間という集合
です。人間には日本人もアメリカ人も含まれます。さらに、埼玉県人や神奈川県人は日本人に含まれます。つまり図で表すと次のようになります。
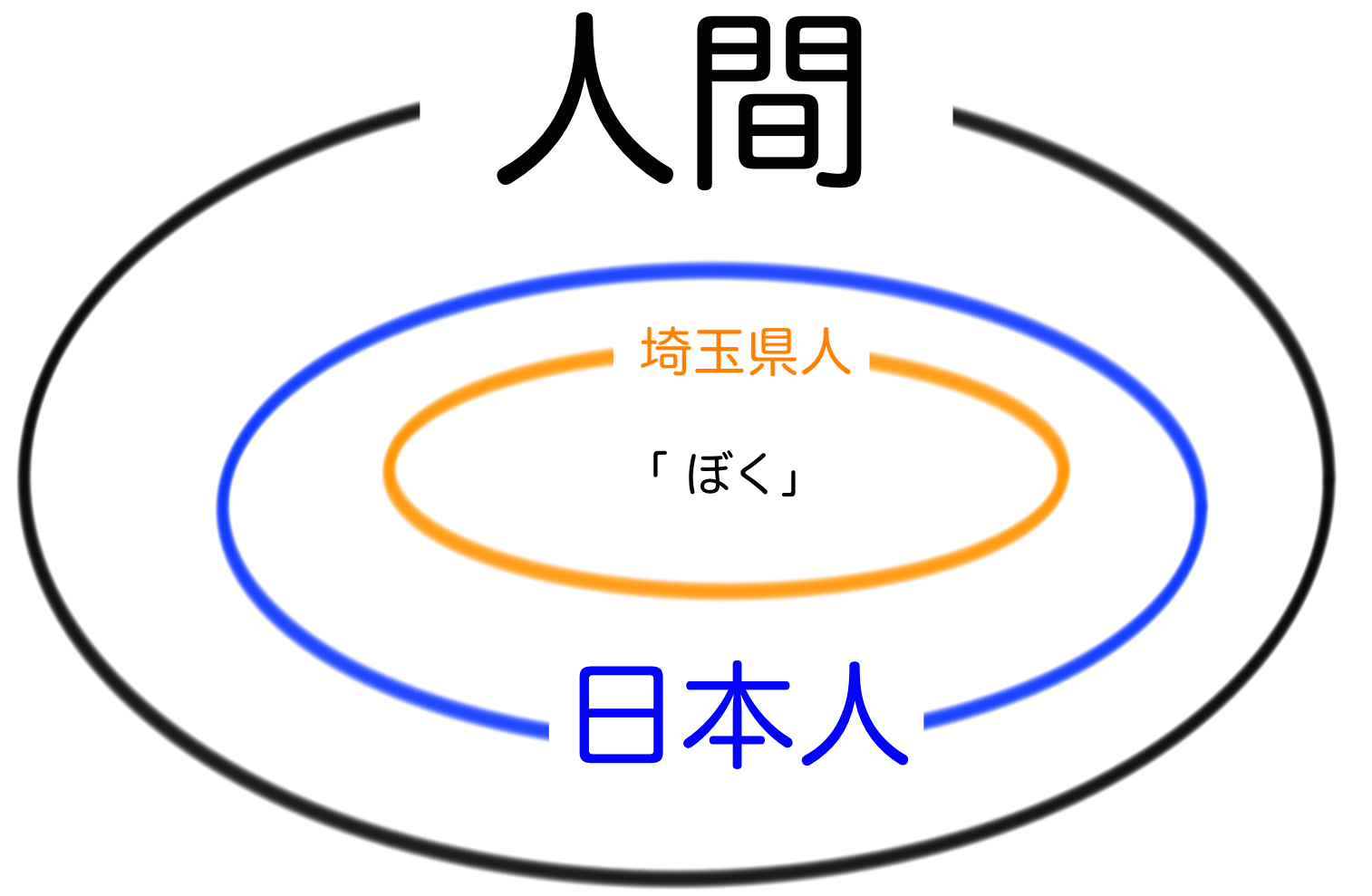
数学で集合が登場したときにはこのように、
どの集合がどの集合に属するのか？？
ということを見極めることが大切です。人間というグループの中に日本人がいる。日本人というグループの中に埼玉県人がいる。といった具合にです。
集合の意味を何となく理解できましたか！？
つぎは中学1年生の数学教科書で登場した「整数の集合」と「自然数の集合」について考えてみましょう。
集合とはグループのことでしたね？？
つまり整数の集合とは
整数の数のグループのこと
です。自然数の集合も同様に、
自然数の数のグループのこと
です。
人間、日本人、埼玉県人、という集合のときと同様に、
「整数の集合」と「自然数の集合」のどちらが大きいか考えてみましょう！！
整数とは…-3, -2, -1, 0, 1, 2, 3…..でしたね？ 自然数とは指で数えられる数1, 2, 3, 4, 5…..です！
数直線で考えてみると次のようになります。
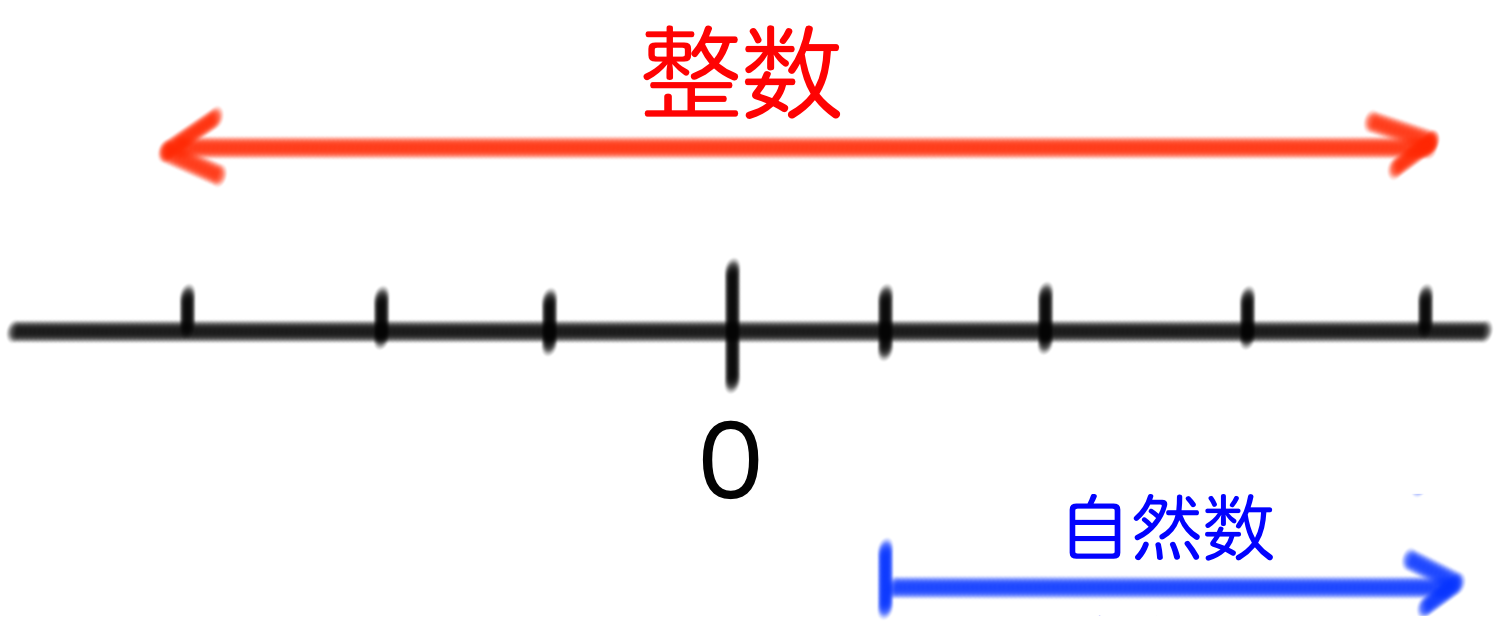
この数直線から視覚的にわかるのは、
「自然数の集合」が「整数の集合」に含まれている
ということです。1という数は自然数でもあり整数でもあります。2も3も同様。
がしかし、-1や0といった数はどうでしょう？？これらは整数ですが自然数ではありません。つまり、整数の集合のほうが自然数の集合より守備範囲が広いんです。
この2つの集合の関係を図にあらわすと次のようになります。
数学の集合では、
どっちの集合がデカいのか！？
という疑問をなげかけることが大切。頭でじっと考えてもわからないときは上のような絵を描いてみましょう！
じつは整数の集合よりも大きな数の集合があります。
それは「数全体の集合」というヤツです。これはいったいどういうことなんでしょうか！？？？
ご存知の通り、整数には分数、小数・・・といった中学数学で登場する数が含まれません。たとえば0.2、
これらは中学数学では「数全体」という集合で表現されます。なぜなら、数字なら何でも「数全体」という集合に属することができるからです。
「数全体」「整数」「自然数」という3つの数の集合の関係をさきほどのように図で表現すると、
という感じになります。
「整数の集合」「自然数の集合」よりも大きな「数全体の集合」を忘れないであげてくださいね！。
もしかしたらテストにひょっこり出題されるかもしれません。
ここまでスピーディーに「整数の集合」と「自然数の集合」の違いを確認してきました。
中学数学で「数の集合」の問題が出題されたら、
どちらの集合がより大きいのか
ということを確認してみましょう。どんな難しい問題でも瞬殺できるはずです。
それでは、また今度です！
Ken
中学校で勉強する数学には「指数の計算」が山のように出没します。
もうその指数の数は多すぎて数えられないほど。中学校の数学が指数で成り立っているといっても過言ではありません。
ところが、です。
中学数学で登場する「指数の計算」にはたくさんの落とし穴が潜んでいます。
はあ？指数の計算！？ラクショーだよそんなの
となめてかかるとゼッタイに痛い目に合います。中間・期末テストでとれたはずの点数が指数計算のケアレスミスによって台無しに。それじゃあモッタイナイですよね？？
そこで今日は、
中学数学の「指数の計算」で注意すべき3つのポイント
をお伝えします。指数の計算が苦手な中学生の方や、これから指数を勉強する数学初心者の方までが参考にしてくださるとうれしいです。
それじゃあさっそく、指数計算で注意すべき点を3つ紹介していきます。ポイントをしっかり押さえて数学テストでのケアレスミスを少なくしましょう。
指数の計算で多くの人が陥りやすい落とし穴は「指数と()」の位置関係の誤解です。これは負の数の指数計算で間違える方が多発するケース。えっ、いったいどんな指数計算の落とし穴なのかですって？？
それは、
負の数の()の外に指数があるか、内に指数があるか計算結果が異なる
ということです。()の外に指数があると、負の数自体を繰り返し掛けていることを意味します。逆に、()の内に指数があると指数がついた数字（低）を繰り返しかけた数に「マイナス記号」をつけていることになります。
ちょっと言葉では言い表しづらいので、実例をもとに確認していきましょう。
たとえば、
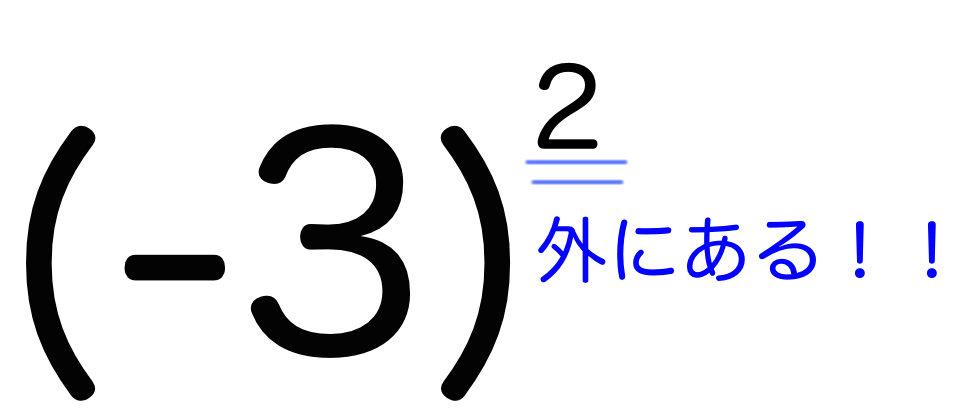
このケースは「()の外側に指数がある」場合です。つまり、（-3）という負の数自体を2回繰り返し掛け合わせた数なので答えは、
それでは
これは先ほどの
そのため、この計算は「3を2回繰り返しかけた数にマイナスの符号をつける」ことを意味します。よって、指数計算の結果は、
以上の2つの指数計算はかなり似ています。もうリリとララぐらい似ています。だって、指数の位置が()の「内」か「外」だけの違いですからね。
負の数の計算で「()と指数の位置」が異なると「計算結果の符号」が異なることを肝に命じておきましょう。
2つ目に気をつけるべきことは「指数の数」です。
えっ。指数の数に気をつけるのは当たり前ですって？？た、たしかに。指数は「同じ数を繰り返しかけあわせる数」です。注意しないわけにもいきません。
ぼくがここで言いたかったのは、
（負の数の指数計算の場合に）指数が「奇数か偶数か」に注意して計算する
ということです。ここで言う「負の数」とは先ほど解説した()の外側に指数が置いてあるケースです。たとえば
となります。説明だけではちょいとわかりづらいので具体例をみていきましょう。
たとえば、
よって、2つの指数の計算結果は、
となります。
この指数の計算例をみても、
となっていることがわかります。ただ、このれは「()の外側に指数があるときのみ」有効になります。指数の計算をする前にはよーーく目をこすっておきましょう。
最後に指数の計算で注意すること。それは
絶対値が1より小さく0より大きい数（0<a<1）の指数計算
です。1よりも小さい数とはたとえば、
ここで覚えて欲しいことは一点だけ。
「1より小さく0より大きい数字」の指数計算をすると、もとの数より小さくなる
ということです。
く、繰り返し同じ数を掛けたんだから大きくなるはず！！
といいたい気持ちは十分にわかります。ただ、「絶対値が1より小さく0より大きい数」にだけは気をつけておきましょう。
たとえば次のような指数の問題があったとします。
つぎの数の大小を比較しなさい。間違えたらビンタします。
と
このとき「2乗したほうが大きくなるはずやろ？？」という固定概念をもっていると、
と思わず答えてしまいそうです。これだと手痛いビンタを頬に食らうことになります。
ここは冷静沈着になって試しに指数の計算をしてみましょう。すると、
となります。これは明からに元の数「0.3」より小さいですよね？？？
よって答えは「
以上で指数の計算で気をつけるポイントは終了です。
たった3つのことを頭にいれておくだけで、指数の計算のケアレスミスを避けることができるのです。中学数学では指数の計算が死ぬほど登場します。指数という言葉で耳鳴りがするほど。
そんだけ頻繁に登場する指数の計算でミスをなくせば、数学テストの点数がグングンと昇っていくでしょう。
それでは、また今度です。
Ken
小学校の算数になかった用語に「指数（power）」があります。
ぼくが中学生になりたての頃、「指数」の意味を理解するのにだいぶ苦戦してました。いやあー辛かったなあ・・・・
指数を理解するのは時間の問題
いや、だけれども、です。
一度、数学の「指数」の意味を理解してしまえばもう怖いものなしです。
中学3年間の数学で、指数がたぶん、10000回ぐらい登場すると思います。 それだけ頻繁に登場する数学用語です。中学1年生の初期から理解しておくことに越したことはありません。が、逆に言えば、別に最初で理解できなくても後々わかっていきます。ご安心を。
この記事では中学数学用語の「指数（しすう）」を5分でわかるように説明していきます。指数を理解できずに苦しんでいる中学生の方なんかが参考にしてくださるとうれしいです。
それでは、さっそく中学数学で勉強する「指数」の意味を確認していきましょう。
指数を理解しやすいようにステップバイステップで解説していきます。
同じ数字を掛ける式って長くてメンドクサイですよね？！
美女に「3を300回かけた計算式を明日までにレポート用紙に書いてきて。約束よ」
と言われてもなかなか厳しいものがあります。なぜなら、300回も3という数字を書きたくないし、×という掛け算の記号も300回はさすがに見たくないからです。数学に詳しくないと素直に、
と苦しく書き写しをせねばなりません。これでは腕力に自信があってもいつか疲れはててしまいます。最悪の場合、腱鞘炎を引き起こしてしまう可能性があります。これはいくらなんでも辛すぎますね。
そこで登場するのが「べき乗 (exponentiation)」という概念です。これはカンタンに言ってしまうと、
同じ数を繰り返し掛ける計算を省略できる
というものです。たとえば、さきほどの「3を300回かけるケース」を例にとりましょう。3を300個、「掛け算の記号」を299回書かなくてもいいんです。「3を300回かける」計算式はつぎのように表すことができます。
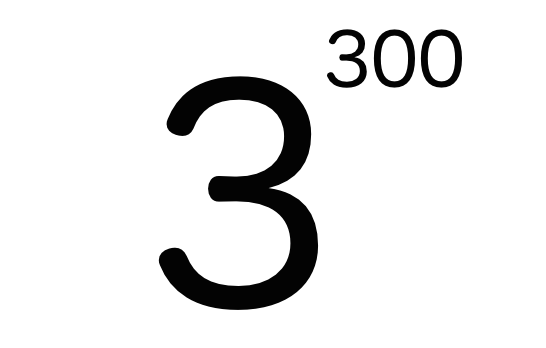
繰り返しかける数の右上に「掛け算を繰り返す回数」を付け足します。「3を300回掛ける計算式」を書いて？と命令されても大丈夫。A4のレポート用紙の半分のスペースがあれば十分です。こいつは楽チン！
ここで登場した「掛け算を繰り返す回数」を「指数」といいます。この例でいえば「300」が指数ですね。ちなみに、これは高校数学で勉強することですが、この指数がついた数字を「底（てい）」といいます。
さて、これで「指数」の正体がわかりましたね！？？
一言で言うと、
同じ数を掛け合わせる回数
ということになります。
それではいったい、新しく登場した「べき乗」の数はどうやって読めばいいのでしょうか？？ 意味はわかったけど、読み方がわからない。
これでは、好きな子ができたけど名前がわからない状態と一緒です。歯がゆすぎます。
いや、しかし、べき乗の読み方はいたってカンタンです。
「AのB乗（じょう）」
と読めば良いのです。ここではAに底（てい）、Bには指数を当てはめます。たとえば先ほどの例で言えば、
「3の300乗（サンノサンビャクジョウ）」と読むわけですね！！なるほど。
でもでも、
いきなりこれが「指数」だい！よろしこ！
なんていわれてもピンと来ませんよね？？ ある日、突然やってきた転校生にいきなり馴染めないと同じ。何か「指数」という転校生を印象づけて覚えなくては・・・・・
今日はせっかくですので、ぼくが中学生のときに指数の意味を覚えた方法を紹介します。よかったら参考にしてください。
ぼくは
「~~~~を~~~~~回かけた数」という念仏をとなえて指数の意味を理解していました。
たとえば、先ほどの「3の300乗」でいえば、
という感じです。独り言を言うのが恥ずかしいという方は、底と指数の間に「ことば」を書き込んでみましょう。ちょうど上のような感じです↑↑
教科書とかプリントが汚くなりそうですけどw
ふう、ここまで中学数学で勉強する「指数」の意味を振り返ってきました。
冒頭で申した通り、中学校の数学には「指数」が頻繁に登場します。そうですねえ、週3日とかの頻度じゃないですかね。
ただ、この記事を読んで指数の意味がわからなくても大丈夫。数学を勉強するにつれて指数の意味をカラダで感じとることができるはずです。焦らずに勉強していきましょう！
それでは、また今度です。
Ken Sawai
中学数学で登場する「逆数」の使い方をマスターしたい。
逆数の計算をものの2秒で終了させたい。
そんな願いを抱えていませんか？？ 逆数の計算をぱぱっと片付けると断然クールですし、何やら異性にモテそうな気がしてきます。
今日は逆数の計算を瞬殺したいと願うすべての中学生の方のために、
【意味から考える】逆数の計算を2秒で片付ける3つの方法
という数学学習の記事を書いてみました。逆数の計算問題をクリアするために、まずは逆数の意味を振り返ります。その後に逆数を計算するおすすめの方法を3つ紹介していきますね。
＜もくじ＞
それではさっそく見て行きましょう。
中学1年生の数学で登場する「逆数（reciprocal）」の意味はいったい何なのでしょうか？？
とりあえず中学校の数学教科書をのぞいてみましょう！
教科書には逆数の説明が以下のように記載されています。
2つの数の積が1になるとき、一方の数を、他方の数の逆数といいます。
なるほど。たとえばAという数字くんがいたとしましょう。そこにBという「たまたま通りがかった数字くん」を掛けてみます。ぐ、偶然にも答えが1となった場合、
BはAの逆数である
といえるわけですね！なるほど！
逆数の意味をなんとなく理解できましたか？？
次は逆数の計算を２秒で片付けるために身につけたい3つの逆数の計算方法を紹介していきます。これから紹介する計算方法はそれぞれ、
の3つです。逆数を計算したい対象によって場合わけしてみました。
よかったら参考にしてみてください。
一番カンタンな逆数の計算は「分数の逆数」です。なぜなら、
分母と分子をひっくり返せばいいだけだから
です。分数の逆数は視覚的にもわかりやすいですし、なによりケアレスミスを防ぐことができます。それでは例題と一緒に逆数の計算方法をみていきましょう。
たとえば、
の逆数を5秒以内に計算せよ。
という計算問題があったとしましょう。このような分数の逆数計算の問題が出題されたら超ラッキーです。なぜなら、
分母と分子をひっくりかえせばよいから
です。この場合ですと、分母の4と分子の3の場所をとっかえっこした、
が答えとなります。ふたつの数字の場所を取っ替えっこするだけなので5秒もかかりませんね。
ただ、分数の逆数計算で注意すべき点が1つあります。それは、
帯分数の逆数計算
です。たとえば、
の逆数を4秒で計算せよ。
という問題があったとしましょう。このとき、先ほどの解き方の通りに分子と分母を逆にした数、
と答えては間違いです。なぜなら、この数はもとの
こういうときは、
帯分数を「帯分数なしの分数」になおす
という作業が必要です。先の例で、
帯分数の逆数の計算には十分に注意しましょう！
つぎに小数の逆数計算方法です。小数の逆数計算方法は以下の手順をふみます。
先ほどの分数の逆数計算方法にワンステップ増えただけですね！とりあえず、小数を分数に直してから分数の逆数計算方法を適用してやればいいのです。
たとえば、
という数学問題が出現したとしましょう。先ほど紹介した小数の逆数計算方法にしたがうと、まずは小数を分数に直さねばなりません。すると、
となります。そのつぎに、分数（もと小数）の逆数を計算してやればよいことになります。すると、0.2の逆数は、
であることがわかります。少々めんどくさいですが、この方法ならば逆数の計算ミスを防ぐことができます！
最後に整数の逆数の計算方法を紹介します。整数の場合、
逆数を計算する整数を分母にし、1を分子にする
という計算方法を利用しましょう。ちょっと文章にするとわかりづらいので実際の例題をみています。
たとえば、
7の逆数を0.1秒で求めよ。
という逆数の計算問題があったとしましょう。このとき、逆数の計算をする数「7」を分母に、1を分子にした分数が逆数になるので、
7の逆数は
ちょっと複雑ですが、コツを掴んで急いでペンを握れば0.1秒ぐらいで逆数を計算できそうですね。
整数の逆数を計算する際、気をつけるポイントが1つだけあります。それは、
負の整数の逆数の計算です。
逆数の意味は、
2つの数の積が1になるとき、一方の数を、他方の数の逆数といいます。
でしたね？？ よって、負の数の逆数は「負の数」にならねばいけません。なぜなら、もとの数に逆数をかけたら正の数1になるようにしたいからです。負の数に負の数をかけたら正の数になりますよね？？ これを忘れずに覚えておきましょう！
以上で逆数の計算のコツの紹介は終了です。この記事では分数、小数、整数の3つの場合に使える逆数の計算方法を書いてきました。
あれ？ 逆数の計算の方法わすれちゃった・・・・
というときは逆数の意味を思い出しましょう。
掛けたら1になる数が逆数！
このことだけを暗記しておけば超十分です。
それでは、また今度です。
Ken
中学数学の単元「正の数・負の数」では、「項 (こう)」という言葉が登場します。
「項」なんて小学校で勉強しなかった数学用語ですよね？
数学が苦手な中学生の方はきっと、ぜんぜん、ピンときてないはず。
そこで今日は、中学数学で登場する「項」の意味を復習していきます。
さっそく、中学数学で勉強する「項の意味」を復習してみましょう。
中学1年生の数学の教科書には「項」の意味がつぎのように紹介されています。
加法だけの式、
$$(+7)+(-8)+(-5)+(+9)$$
で、
$$+7, -8, -5, +9$$
を、この式の項（こう）といいます。
つまり、
ある式を「足し算だけ」の式に直したとき、＋記号に挟まれてる奴らが項なのです。
たとえば、
$$2-8+7$$
という式があったとしましょう。
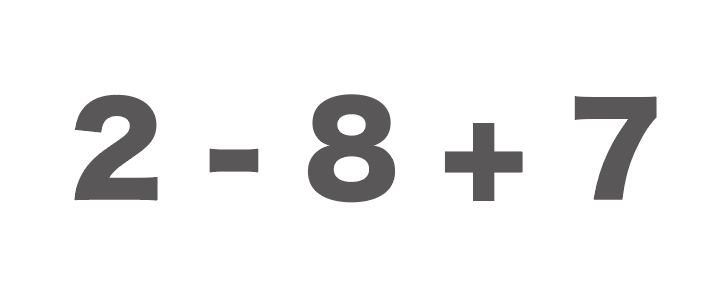
このとき、この式を加法（足し算）だけの式に直してみると、
$$2+(-8)+7$$
になりますね。
そのため、この式の項は、＋記号にはさまれている３つの塊である、
になるわけです。
だいたい項の意味もわかってきましたが、あと注意することが一点。
それは、掛け算・割り算が混じっている場合の項の見つけ方です。
掛け算・割り算が混じっている式の場合は、
掛け算や割り算を一度計算してしまってから、項を探すようにしましょう。
たとえば、
$$2 × 3 -3 ÷ 6 × 2 – 7$$
という式があったとしましょう。
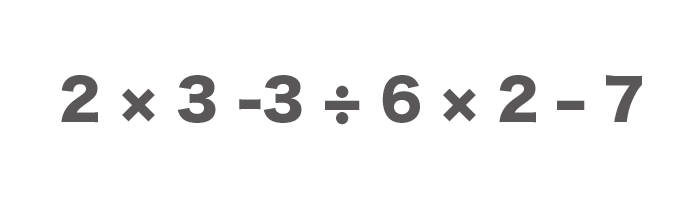
こんな感じで、掛け算と割り算が入り乱れている式の場合は、
まずは掛け算割り算を計算します。
すると、
$$2 × 3 -3 ÷ 6 × 2 – 7$$
$$= 6 -1 -7$$
となりますね。
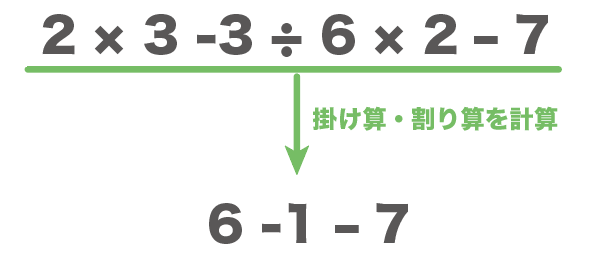
ここまでくれば、先ほど同様に、式を足し算だけの式に直してあげればいいので、
$$6 -1 -7$$
$$= 6 +(-1)+( -7)$$
となります。
結論、この式における項は、＋に挟まれている、
の3つということになります。
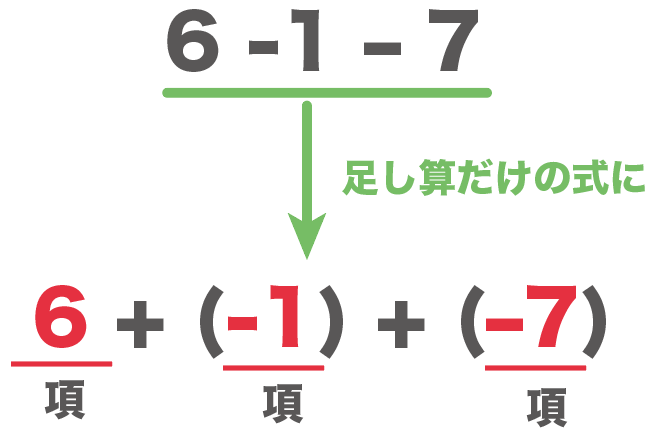
以上が、項の意味でした。
最後に復習しておきましょう。
項とは、
足し算だけの式に直した時に、＋記号に挟まれている塊のこと
でしたね。
だから、とある式で項を探したいときは、まずはその式を足し算だけの式に書き換えてみればいいのです。
項はこれから３年間活躍する重要な数学用語なのでしっかりここら辺でマスターしておきましょう。
それでは！
Ken
中学数学を勉強し始めて最初にぶつかる壁があります。それは、
マイナスかけるマイナスはなぜプラスになるのか？？
ということです。ゼロより小さいマイナスの数をかけたら、なぜ計算の答えがもとの数より大きくなってしまうのか？？ 不思議すぎます。
こんなことが許されるなら、借金（マイナスのお金）に借金をかけ合わせればプラス、つまりお小遣いになりそうです。
そんなのゼッタイおかしいですよね？？
そこで今日は「マイナスかけるマイナスがなぜプラスになるのか？？」という全国の中学生の疑問に答えるために解説してみました。
答えが気になって夜も眠れない中学生の方！！ぜひ参考にしてみてくださいね。
まずは正の数と正の数のかけ算の場合を考えてみましょう。小学校で勉強した算数の延長ですね。たとえば、
という計算式があっとしましょう。小学二年生で勉強した九九で瞬殺すると、2秒でこの答えが6であることがわかります。だって、「サンニガロク！」ですからね。
で、でもちょっと待ってください。
そもそも「掛け算」って何でしょうか？？ うまく説明できるでしょうか？？
ぼくは「掛け算」は次のような計算のことだと思っています。それは、
「ある数のセット」を「ある方向」に「掛ける数ぶん」だけ0から増やす行為
です。えっ。ぜんぜんわかりませんですって？？！ そんな方のために先ほどの「
この計算式では「3という数字セット」を「そのままの方向」に「2つ」増やしています。もうお分かりですよね？ 赤字の文章と対照させて考えると、
「3という数字セット」=> 「ある数のセット」
「ある方向」=>「そのままの方向」
「2つ」=>「掛ける数ぶん」
となります。数直線を使って視覚的に考えてみるとこうなります。
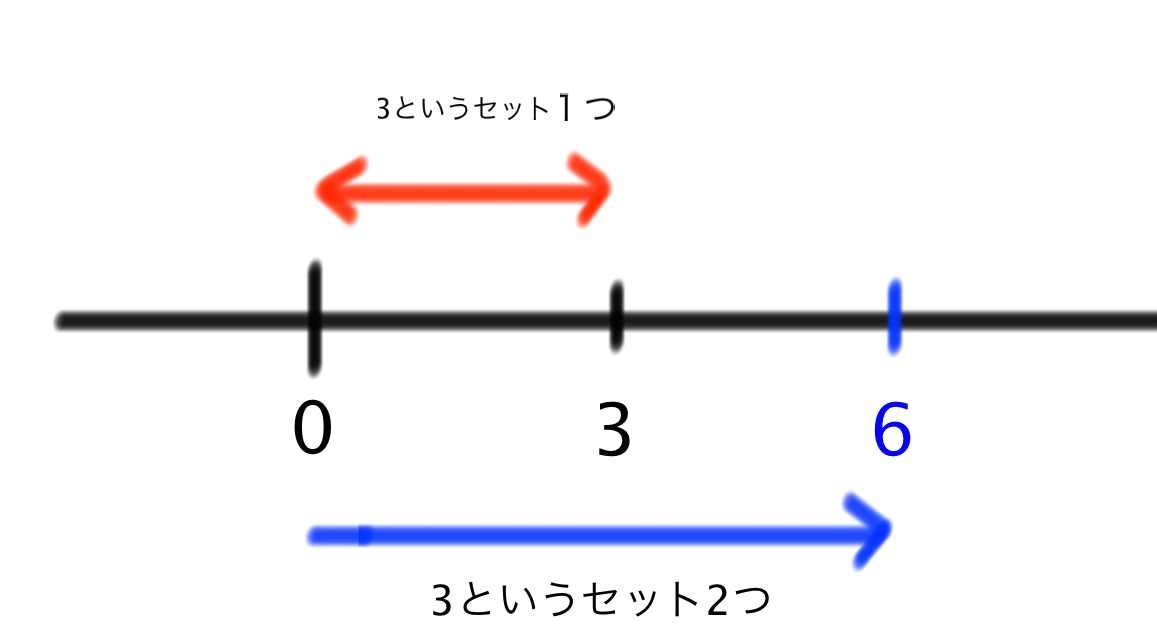
3という数のセットを正の数に2つぶん増やした数。それが答えの6になります。
これが「正の数」×「正の数」の掛け算の場合ですね。
つづいては正の数に負の数（マイナス）をかけた場合です。プラスとマイナスの掛け算はどういう結果になるでしょうか？？
今度は
「ある数のセット」を「ある方向」に「掛ける数ぶん」だけ増やす行為
を掛け算だとすると、この計算式は、
「3という数のセット」を「逆の方向」に「2つ」増やす
と答えが算出されることになります。なぜここでは「ある方向」が「逆の方向」なのでしょうか？？
それは、
掛ける数がマイナス（負の数）だからです。
×の前の数字にマイナスがついていたら逆の方向に数のセットを増やさなければいけません。よって、この掛け算の結果は負の数の「-6」になります。
ここで大切なのは、
マイナスを掛けると逆方向に数字セットを増やさなければならない
ということです。ここをしっかり押さえておけばどんなマイナスの掛け算にも対処することができますよ。
さて、お待ちかねの「マイナスかけるマイナスはなぜプラスになるのか」ということを見て行きましょう。ちょっと難しく見えますが、基本は上であげた2つの例と変わりません。
「ある数のセット」を「ある方向」に「掛ける数ぶん」だけ増やす行為
が掛け算ということを押さえておけば十分です。それではマイナスの掛け算の例題を見て行きましょう。たとえば、「
これは-3というマイナスの数に-2というマイナスの数を掛けています。掛ける数の符号がマイナスであること注意すると、
「-3という数字セット」を「逆の方向」に「2つ」だけ増やす
とこの計算式の答えをゲットできます。やりましたね！数直線で考えてみると、
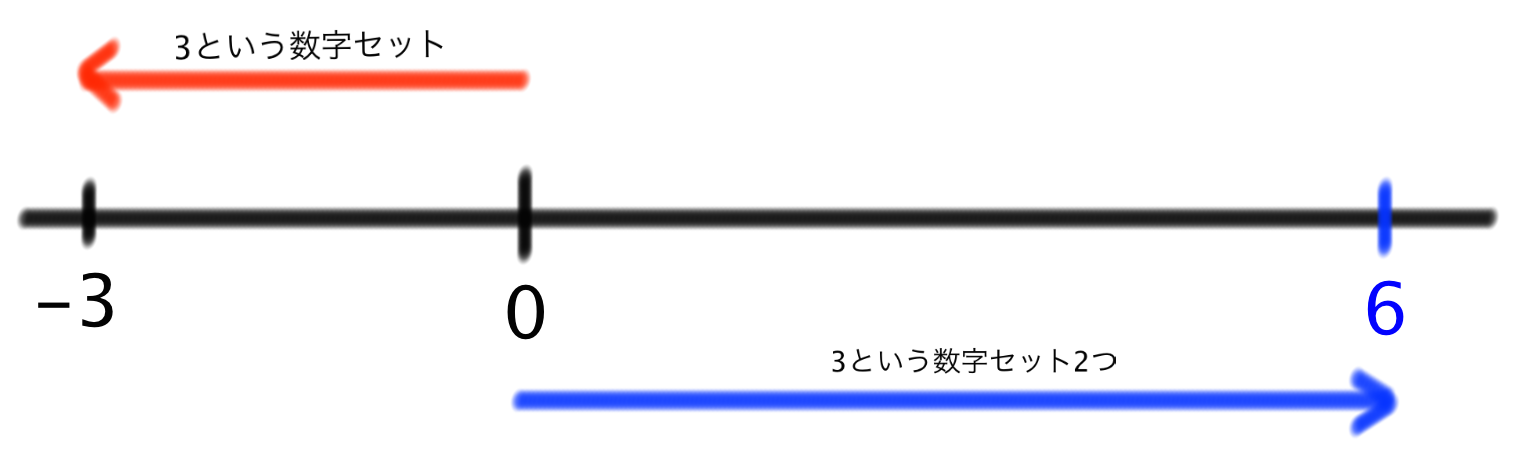
このようになります。マイナスの数字セットである(-3)を「負とは逆方向」に2つ増やします。
したがって、計算の答えはプラスの「6」ということになります。
えっ。いちいち数直線を考えるのがメンドクサイですって？！？ そういう横着な中学生の方は「マイナスとマイナスをかけるとプラスになる！」という事実を暗記しておきましょう。そうすれば一瞬でマイナス同士の掛け算を計算できますね！いやあー便利便利。
ここまで「プラス×プラス」、「プラス×マイナス」、「マイナス×マイナス」という3つのパターンの掛け算をみてきました。ただ、これらすべてのパターンを暗記するだけだと計算の限界があります。
なぜなら、
項が3つ以上の掛け算（乗法）に対応できないから
です。たとえば、
あれ？ マイナスかけるマイナスかけるマイナス？？？ ちょ・・・ちょっと待ってよお・・・
なんて事態になりかねません。そこで登場するのが、
乗法の計算式に含まれる「マイナスの項」を数える裏技
です。マイナスの数が「偶数」と「奇数」の2つの場合で計算結果の符号が変わるとおぼえておきましょう。
という具合にです。たとえば、
また、
えっ。この裏技が使える理由を知りたいですって？！？
そうですね。これは負の数を掛けると「逆の方向に数のセットを増やす」という掛け算の性質のためです。つまり、負の数がひとつ増えるごとに逆の方向に増やさなくてはなりません。
そうですね、電車の線路の方向を切り替えるようなイメージです。もしくは、ネッシーの首を交互にひねるような感覚です。も、もしくは、好き・嫌い・好き・嫌い・・・のような花占いのものです。
これは中学数学を通して頻繁に出題される問題です。しっかりと頭にたたき込んでおきましょう。
それでは、また今度です。
Ken
