こんにちは、こんにゃくゼリーにはまってるKenです。
「資料の活用」で「代表値」が登場します。
「代表」と聞くと、サッカーや野球を想像しちゃいますよね?!?
いえいえ。
数学の「代表値」はまったくスポーツとは関係ありません。

今日は、中学生のために代表値を徹底解説します。
代表値にピンと来てないときは読んでみてくださいねー。
~もくじ~
代表値とは、
データから考えをのべるときに参考する代表的な値のこと
です。
ただ、データをぼーっと眺めるだけじゃ何も生まれないですよね?? 暇つぶしにはちょうどよさそうですけどね。
だから、
データを活用するためには眺めてるだけじゃダメなんです。
何か、自分の考えをつけたさなければデータに意味がありません。
データに自分の考えをつけたすときに参考にするのが「代表値」だというわけです。
「データを代表した1つの値」を参考にして意見を述べる。代表値はデータに価値を出すための材料なんです。
代表値とはなにか??
ちょっとまだピンと来てないですか?!
代表値の理解を深めるために例をみていましょう。
代表値の例として「平均値」をみましょう。詳細は「平均値の出し方」の記事を参考にしてくださいね。
さて、今回の期末テストで上の表のようなテストの結果が得られたとします。
このときの平均点は、
です。
あれ?? 代表値ってデータに意見をつけたすための材料でしたよね?? だけど、5教科の平均点だけじゃ何もわかりません。
でもでも、たとえば、
この点数を「学年の平均点(5教科)」と比べたらどうでしょうか???
学年平均が50点だった場合、
同い年の生徒と比べるとけっこういい成績をとっている!
と意見をいえますよね!あ、たとえば親御さんとかに。
だがしかし、学年平均が98点だった場合。とんでもなくテストが簡単だったんでしょうね。
そんなときは、
テストが簡単だったけど、うまく点数がとれなかった
という意見をいえますね。ただ、これは非常に都合が悪いので、大抵の生徒は隠すでしょう。
こんな感じで、
平均点という代表値を2つ以上出してくれば、データに「考え」や「意見」を付け足せます。
これが代表値の強みというか役割です。
えっ。まだ代表値にピンときてないですって?!?!
次回は「代表値の求め方」を解説していきます。よかったら参考にしてくださいね。
そんじゃねー!
Ken
こんにちは、ヨガにはまりそうなKenです。
中1数学で「相対度数」を勉強します。
相対度数ってよくわからないですよね??
相対? へ? 度数!?

今日は、
「相対度数の求め方」
を解説します。よかったら参考にしてください。
~もくじ~
相対度数とはずばり、
「ある階級の度数」の「度数合計」に対する相対的な割合
のことです。
ぜんぜんわかりませんね。
言葉をいいかえれば、
「ある階級の度数」が度数全体の何%をしめるのか、
ということを表したものです。
度数の求め方は以下のようになります。

ちょっとピンとこないので例題をみてみましょう。
たとえば、以下の度数分布表があったとします。
これはマメつかみゲームの結果。

せっかくなので度数分布表にしてみました。
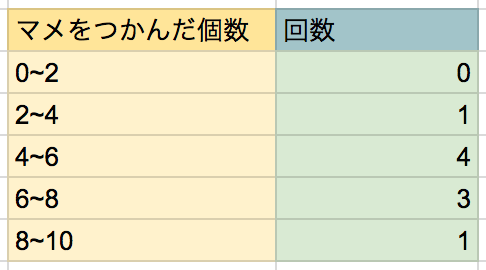
ここでいう「マメをつかんだ個数」が階級、その階級にあてはまるゲームの回数が「度数」ですね!
それじゃあ、ついでのついでに度数分布表で相対度数を計算してみましょう。
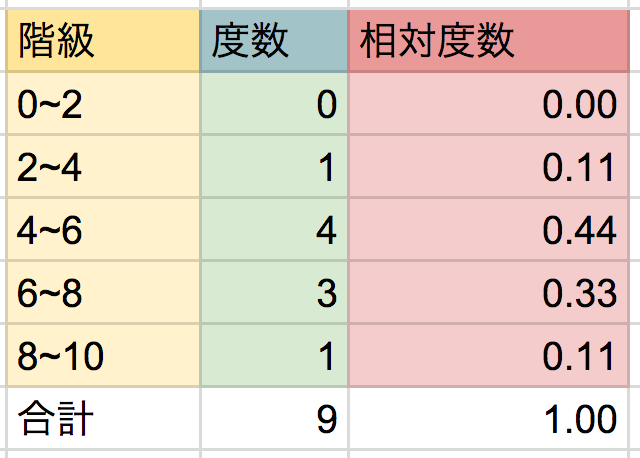
度数をぜんぶ足すと「9」になります。
この「度数の合計」の9で、各階級の度数をわれば「相対度数」が計算できるわけですね!!
たとえば、階級が「0~2」の相対度数。度数は0ですので相対度数は「0.00」になります。
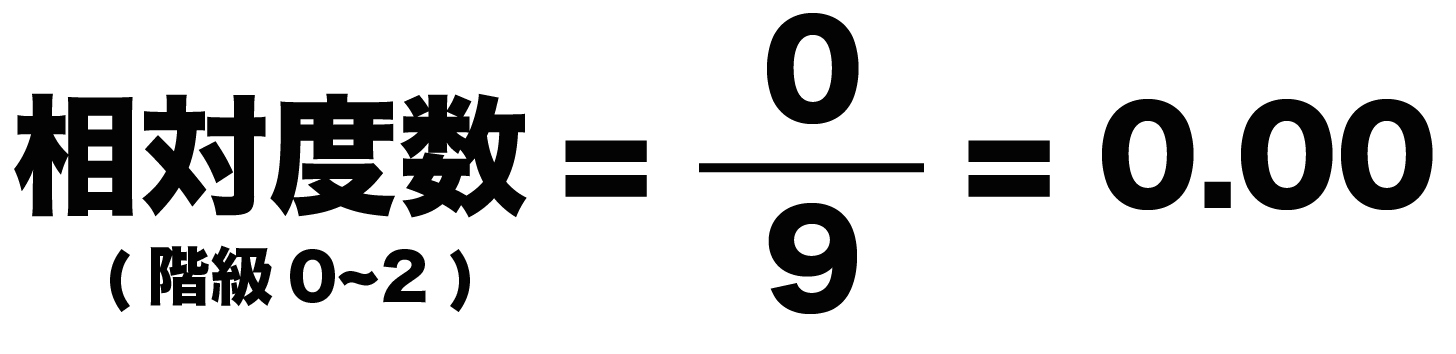 同じように、階級が「2~4」のときの相対度数は、
同じように、階級が「2~4」のときの相対度数は、
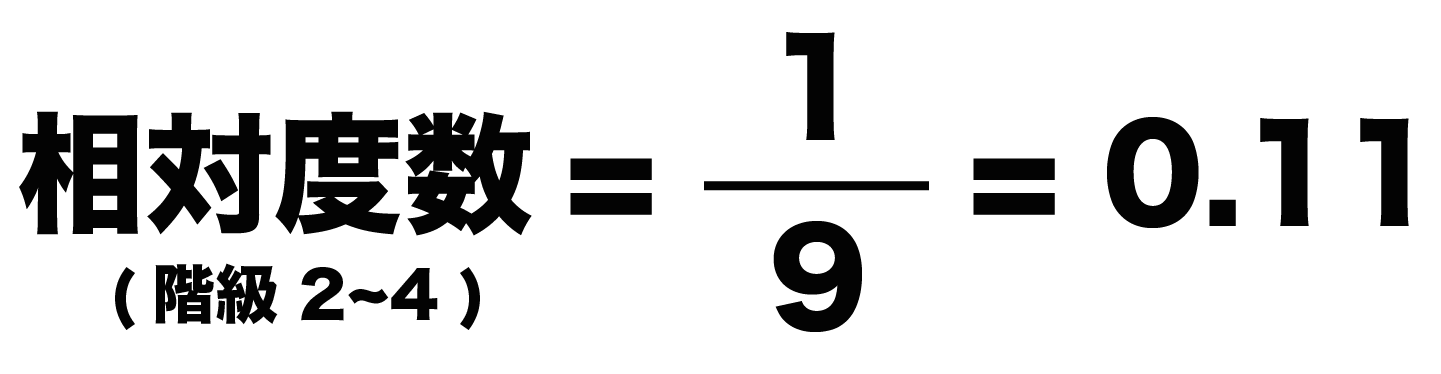
0.11となります!!
こんな感じですべての階級の度数の「相対度数」を求めてやればいいわけですね。
「相対度数を求め方」で気をつけるべき2つのポイントをお伝えします。
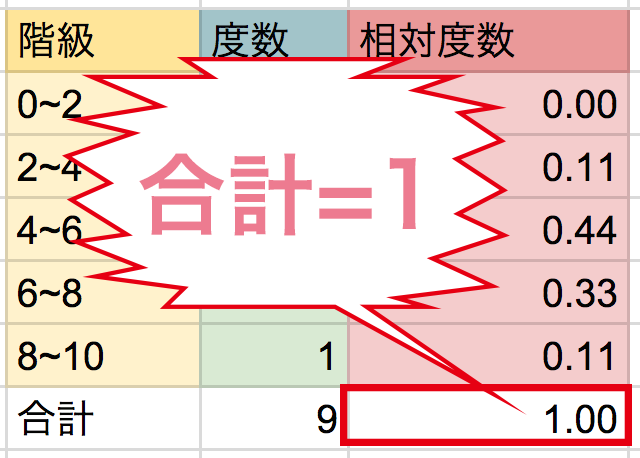
相対度数の合計は「1」になります。先ほどの例でも、
 かお
かお
相対度数の合計が1になっていますよね??
相対度数の問題では「合計が1になっているか」確認しましょう!
相対度数のケタ数に注目してください。
相対度数は割り切れない小数になることが多いです。そのため、
相対度数をどこで四捨五入するか??
ということが重要になってきます。
指定してあれば、その「ケタ数」になるように四捨五入をしましょう。もし相対度数のケタ数について何も書いてない場合。
そのときは、周りの様子をうかがう作戦にでましょう。
大抵、相対度数は以下のような度数分布表の穴埋めで出題されます。
階級が「4~6」の相対度数はいくつですか!?!
といった具合です。
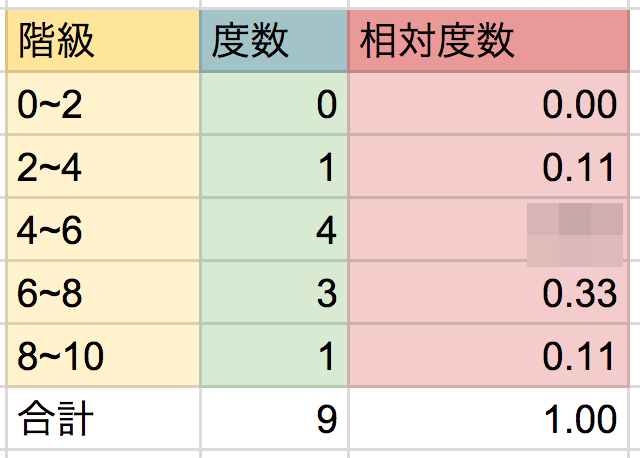
虫食いになっている以外の「相対度数」のケタ数をみてみると、
小数第二位
までケタ数が表示されていますね!?? ってことは、穴埋めになっている相対度数も小数第二位でいいはずです。
相対度数の合計は1になるので、そこから他の相対度数の合計を引いてやるとモザイクの数が出ます。
(相対度数の合計)-(モザイク以外の相対度数)= 1 – (0.00 + 0.11 + 0.33 + 0.11)
= 0.45
よって、モザイクに入る数字は、
0.45
となります。
相対度数の求め方を勉強してみました。
むずかしく聞こえますが、案外カンタンそうで安心ですね!
次回はいよいよ「代表値の求め方」を解説していきますねー。
そんじゃねー
Ken
<<関連記事>>
中1数学で「階級値(かいきゅうち)」を勉強します。
階級値ってリッチな響きしません??。 ただ、階級値ってカンタンでとっつきやすい用語なんです!
今日は、そんな「階級値」くんを解説していきます!
テスト前によかったら確認してみてくださいね。
~もくじ~
中学数学にでてくる「階級値」とはずばり、
階級の端と端のまん中の値
です。階級とは度数分布表における「あるデータの範囲」のことでしたね??

データの範囲であるため、階級は「○○~□□」というように2つの端となる数字が存在します。

つまり、この「0~2」という階級の「階級値」は0と2の半分。両方をたしたものを2で割ればいいわけです。
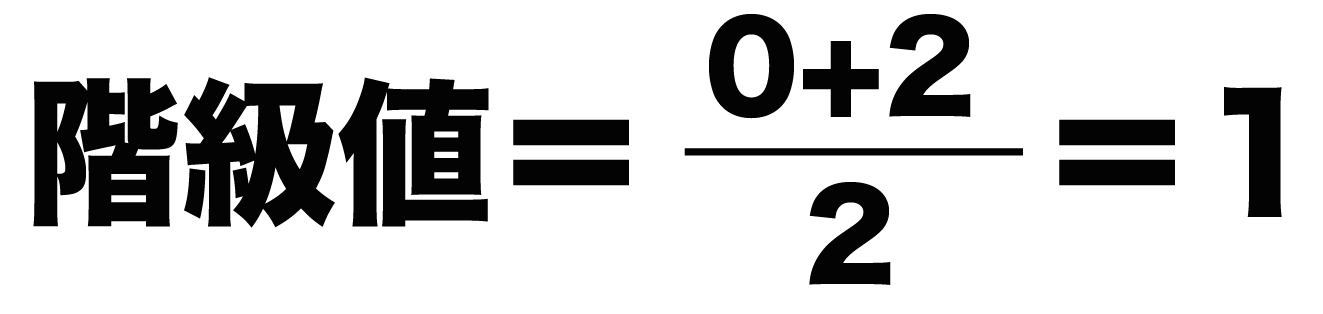
うぬ、思ったより「階級値」もカンタンでしたね!?。
階級値の計算方法はわかりましたね!
ただ、ひとつ疑問なのが、
なぜ「階級値」が必要なのか??
ということです。
階級値はおもに、
度数分布表の平均値をだす
ときに使います。

たとえば、上の度数分布表の平均値を求めたいとき。
ゲーム結果が「4~6」個のときは4回あった、ということはわかります。だがしかし、1つ1つのデータの記録ってわかりませんよね?
階級にあてはまるデータ値がすべて「階級値」だったとすれば、
次のように度数分布表の平均値を計算できます。「階級値×度数の合計(53)」を「度数の合計(9)」でわればいいんですね!
つまり、平均すると5.89個のマメをつかめていた!というわけですね。
以上で階級値の解説は終了です。
階級値の求め方はシンプル。度数分布表の平均値を出すときに使えばいいんですね!
じゃんじゃん階級値を利用していきましょう。
階級値の求め方の動画も作ってみたので良かったら参考にしてくださいね。
そんじゃねー!
Ken
<<関連記事>>
こんにちは、家で凍えそうなKenです。
中1数学の「資料と活用」で勉強する大切なことといえば、
平均値の出し方
です。平均値の出し方をしっていると日常生活でかなり役立ちます。
たとえば、テストの平均点だったり、1年のおこづかいの平均額などなど。
平均値を知っておくにこしたことはありません。

そこで今日は、
3分でわかる!平均値の出し方
を伝授しますよ!
あるデータにおける平均を求める式は、
です。「データの値をすべてたしたもの」を「データ数」でわればいんですね!
たとえば、期末テストの平均点を出してみましょう。
学期末テスト(5教科)の点数がつぎのような場合。
さっき紹介した「平均を求める式」で計算してみましょう。
「データの数」は、国・数・英・理・社の5つですよね!?
そんで、
「データの合計値」は、
国語67+数学89+英語47+理科97+社会72 = 372
になりますね!
よって、テストの平均値は次のようになります。
どんな平均値でも出せそうですね!
「平均値の出し方」の式をおぼえていればマッタク問題ありません!
平均値の出し方がわかれば「資料の活用」なんて怖くないです!
じゃんじゃん資料を活用していきいましょう!
それではー!。
Ken
<<関連記事>>
こんにちは、風が強くて鼻水がとまらないKenです。
中1数学の「資料の活用」で、
度数の求め方
を勉強します。度数って強そうなイメージですよね?? ただ、案外、度数ってたいしたことないんです。すぐに求めることができますよ。

~もくじ~
度数の求め方を確認する前に、
度数とはなにか??
ということを復習しましょう。
度数とは、
ある階級にあてはまるデータの個数
のことです。ちょっとよくわからないので例題とともにみていきましょう。
たとえば、ぼくが「マメを箸で掴んで運ぶゲーム」を体験したとしましょう。すると、次のようなデータが得られました。
ぜんぶで10回ゲームをしたときの結果の表ですね。
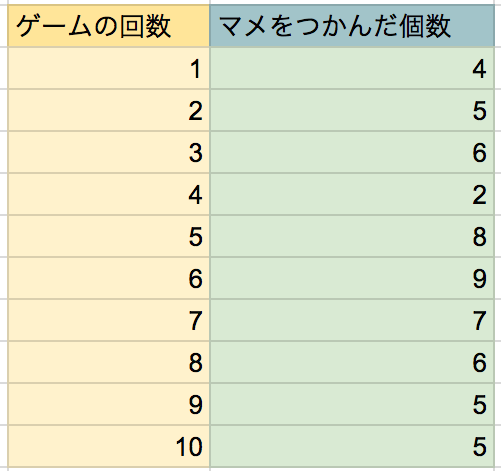
このデータからぼくのゲーム成績をだすために、
0~2回つかめたゲームは何回??
2~4回つかめたゲームは何回??
というように、何個つかめたゲームが多かったのかということを調べていきます。
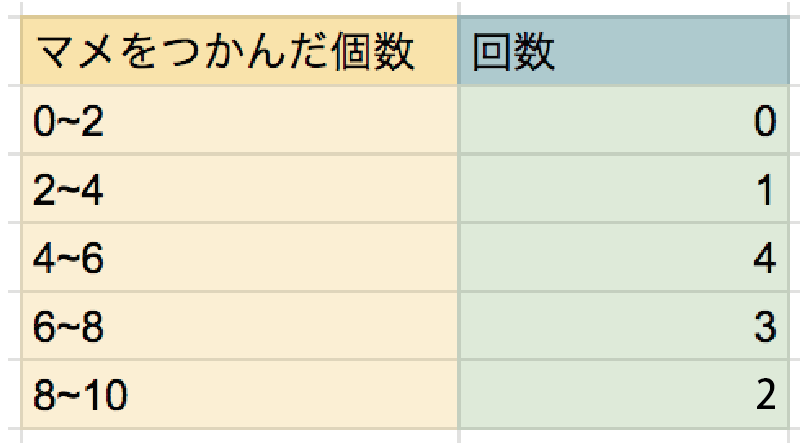
このとき、マメをつかめた個数の範囲を「階級」といい、
階級にあてはまるデータの個数を「度数」といいます。
あまりむずかしくなさそうですね!?
「度数の求め方」は1つしかありません。
階級にあてはまるデータの数を数える!!
これにつきます。
さきほどの例だと、
0~2個つかめたときのデータ数は・・・0、
2~4個つかめたときのデータ数は・・・1、
4~6個つかめたときのデータ数は・・・4、
・・・・・・・・・・・・
というようにじゃんじゃんデータの数を数えていきます。
ある階級にあてはまるデータ数が「度数」ですよね?? つまり、数えるだけで度数を求めることができるんです。思ったよりもカンタンですね。
ただ、1つだけ「度数の求め方」で注意点があります。それは、
階級の区間の範囲
です。○○〜□□とあるけど、○○は階級の区間内のなのか?? □□はどうなのか?? これを知っていなければいけないです。
基本的に階級は、
前の数字「以上」、後ろの数字「未満」となっています。

「○○以上」というときは「○○」も範囲にふくまれます。
逆に、
「○○未満」というときは「○○」は範囲外ですので気をつけてくださいな!
以上で度数の求め方は終了です。
これからじゃんじゃん度数を求めていきましょう!!
そんじゃねー!
Ken
こんにちは、こぶしが痛いKenです。
中1数学の「資料の活用」で、
度数分布多角形
が出現します!漢字が7文字もあってむずかしそうですよね??

いや、いやいやいや。
度数分布多角形なんてぜんぜん難しくないんです。
今日は「度数分布多角形」を徹底解説します。
度数分布多角形とはずばり一言でいってしまうと、
ヒストグラムを折れ線グラフにしたもの
です。
ヒストグラムを、
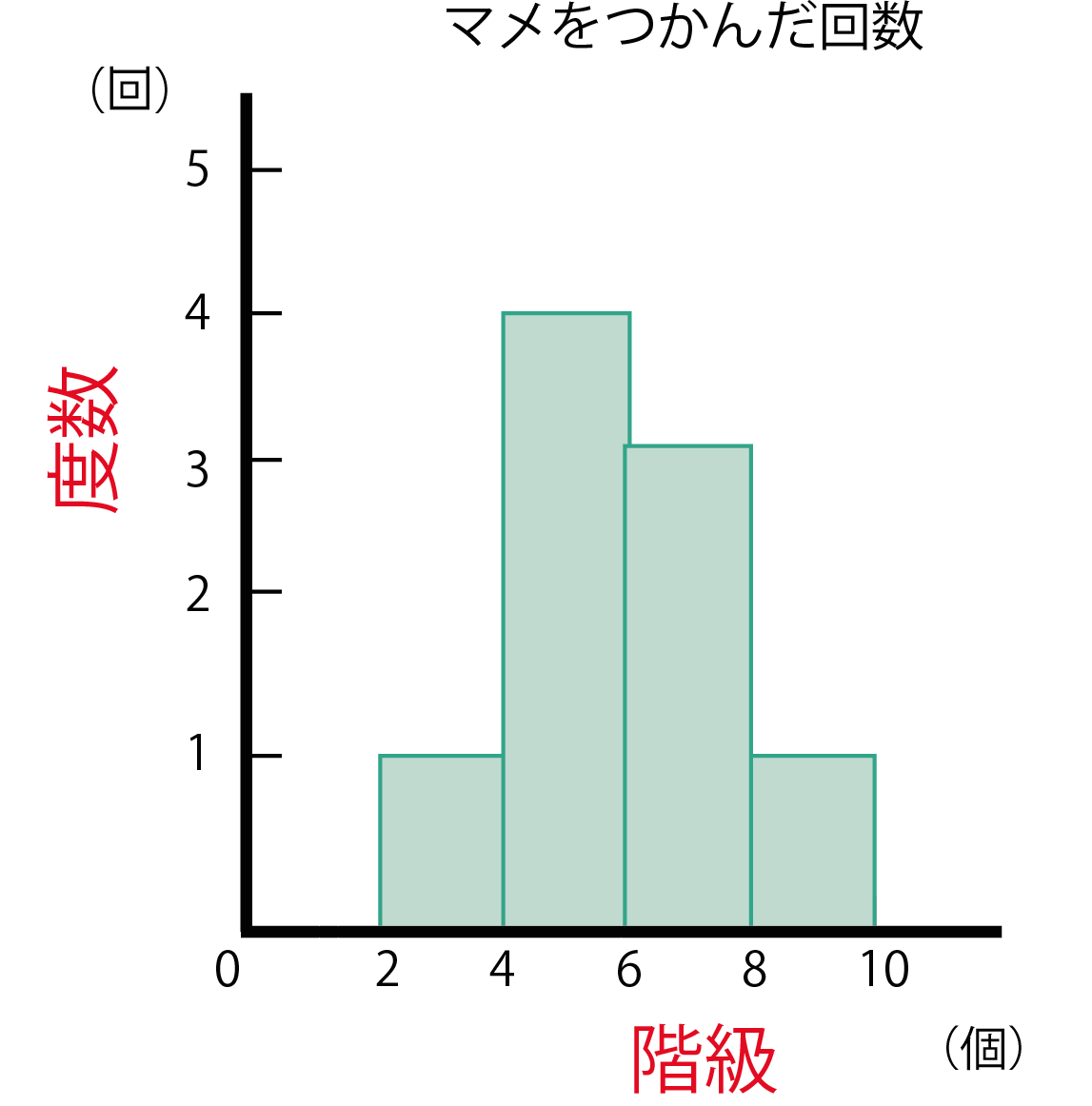
ヒストグラム
折れ線グラフにしたもの!
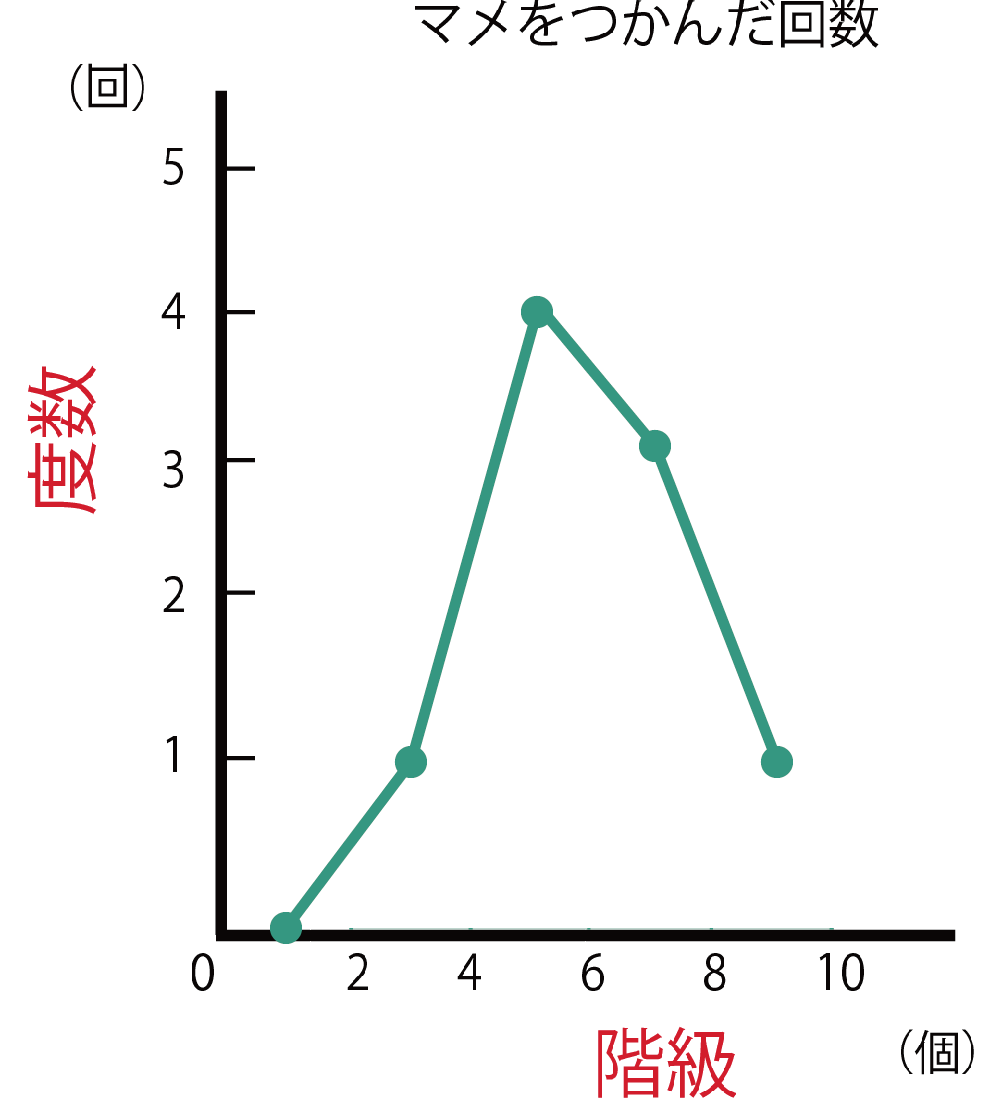
です。ね!そんなにむずかしくないでしょ!?
度数分布多角形の書き方はほんの2ステップしかありません。すぐに覚えられます!
ヒストグラムに長方形がありますよね?!?
まずは長方形の上辺に注目してください。上辺とは「上の辺」のこと。上辺のちょうど真ん中にあたる「中点」に点をうってみてください。
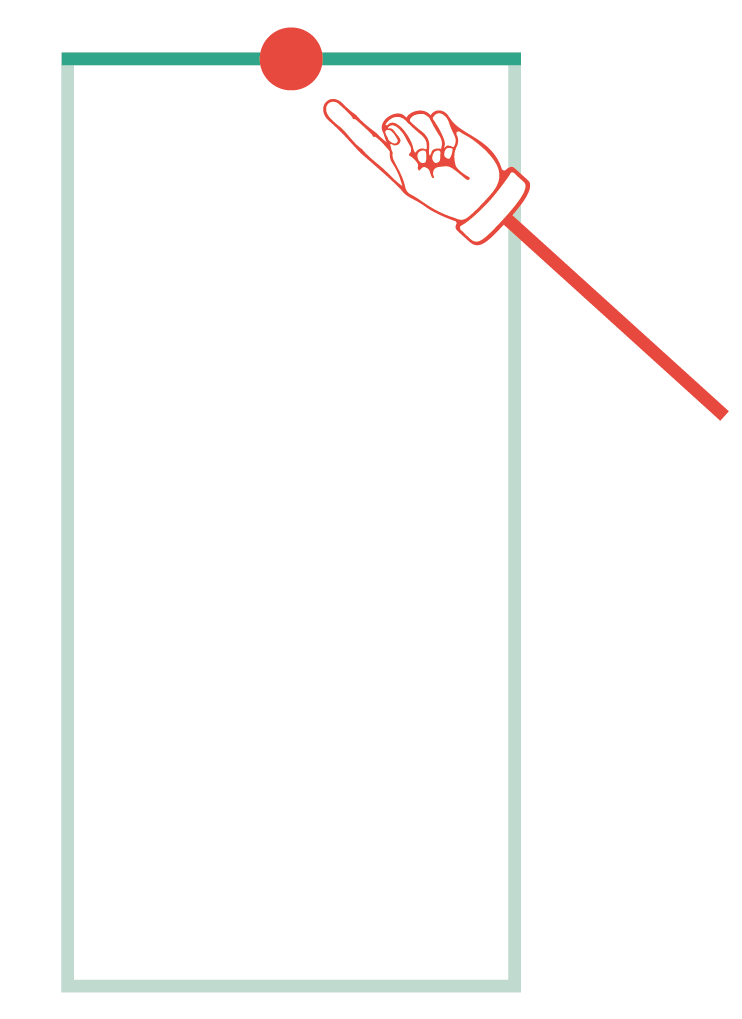
すると、ヒストグラムがこんな感じになるはずです↓↓
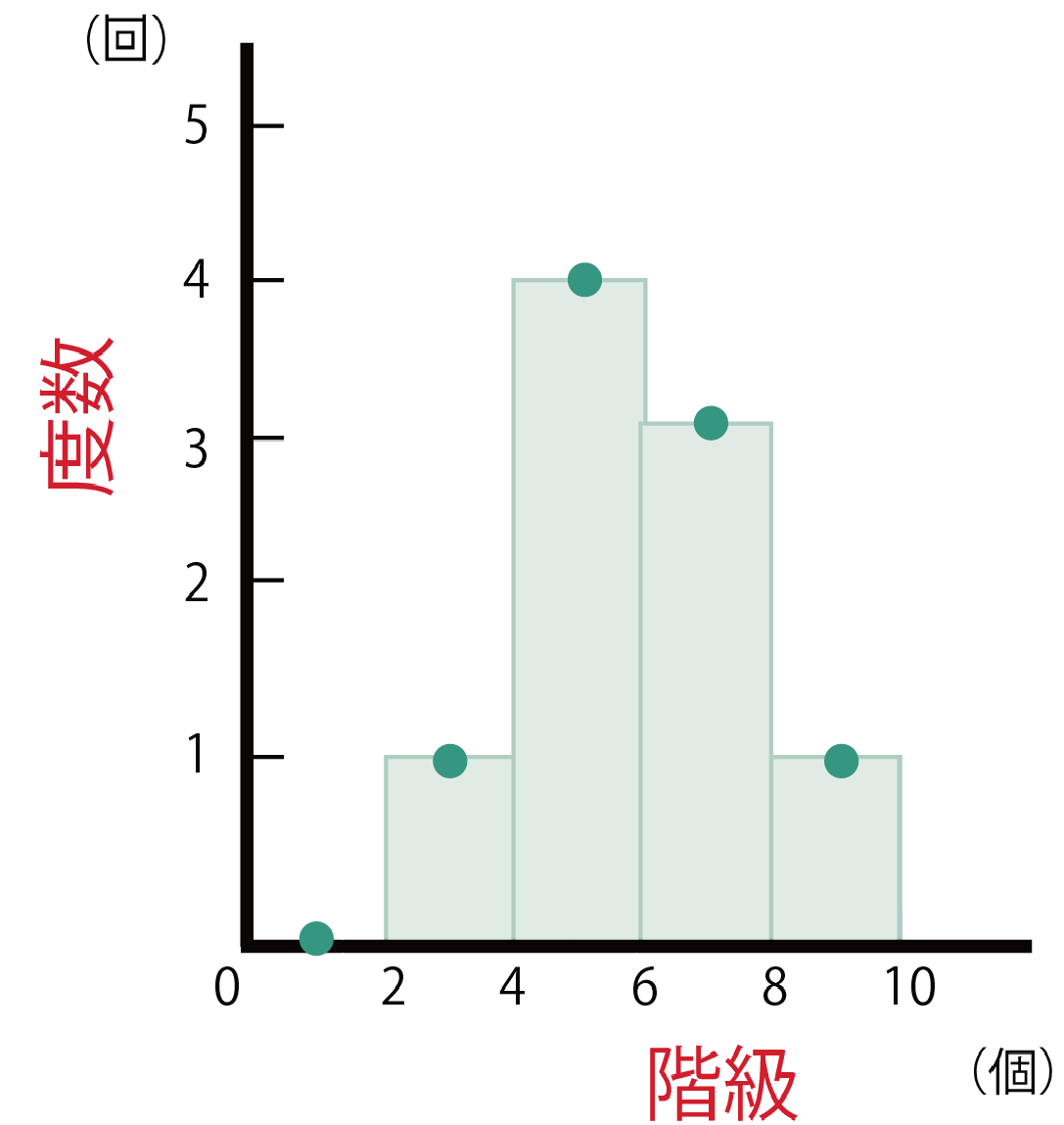
さっきうった点を線でむすびます。するとこうなりますよね??

あ、ちゃんとヒストグラムの長方形は消してくださいね!これでヒストグラムから度数分布多角形をつくれました。なにも問題ありませんね!
資料の活用のテストで度数分布多角形は頻出します。
しっかりと押さえておきましょうね。
そんじゃねー!
Kenny
<<関連記事>>
こんにちは、レベニラ定食を愛してやまないKenです。
中学1年生の単元「資料の活用」で、
ヒストグラム
という数学用語が登場します。カタカナばっかでなんだか強そうですね。? ただ、みかけによらずヒストグラムくんは案外たいしたことないんです。

今日はわかりやすい例といっしょに「ヒストグラム」について解説していきます!
~もくじ~
ヒストグラムとはずばり、
「度数分布表」を棒グラフにしたもの
です。
えっ。度数分布表がよくわからないですって!?? そんな方は【資料の活用】度数分布表の「階級・度数」ってなに??という記事を参考にしてくださいね。
たとえば、度数分布表ってこんな感じのやつです。これはマメをつかむゲームの結果を度数分布表にしたものです。

ヒストグラムではグラフの横軸に「階級」、縦軸に「度数」をとります ↓↓
どのようにヒストグラムを作ることができるんでしょうか?? 今日はヒストグラムの書き方を伝授します。
ヒストグラムの書き方は以下の4つのステップですよ。
ヒストグラムでは横軸に「階級」、縦軸に「度数」をとるんでしたね??
さきほど登場した度数分布表からヒストグラムをつくってみましょう。

すると、
こんな感じで縦軸と横軸がかけそうですね!
ヒストグラムに縦軸と横軸の目盛りをふっていきましょう!
ヒストグラムの横軸は1つの「階級」ごとに目盛りをいれて、
縦軸は、「度数の最大値と最小値がおさまるよう」に目盛りをふりましょう!
さっきの例でいえば、
階級は「0~2」、「2~4」・・・というように2つずつ変化していますよね?? そのため、ヒストグラムの横軸の目盛りは2ずつとっていきます。こんな感じです↓↓
そんで、次は縦軸の「度数」ですね!
度数分布表をみると、度数の最小値は「0」、最大値は「4」です。0~4までの数字がおさまりそうな、0から5までの目盛りを縦軸にふってみます。
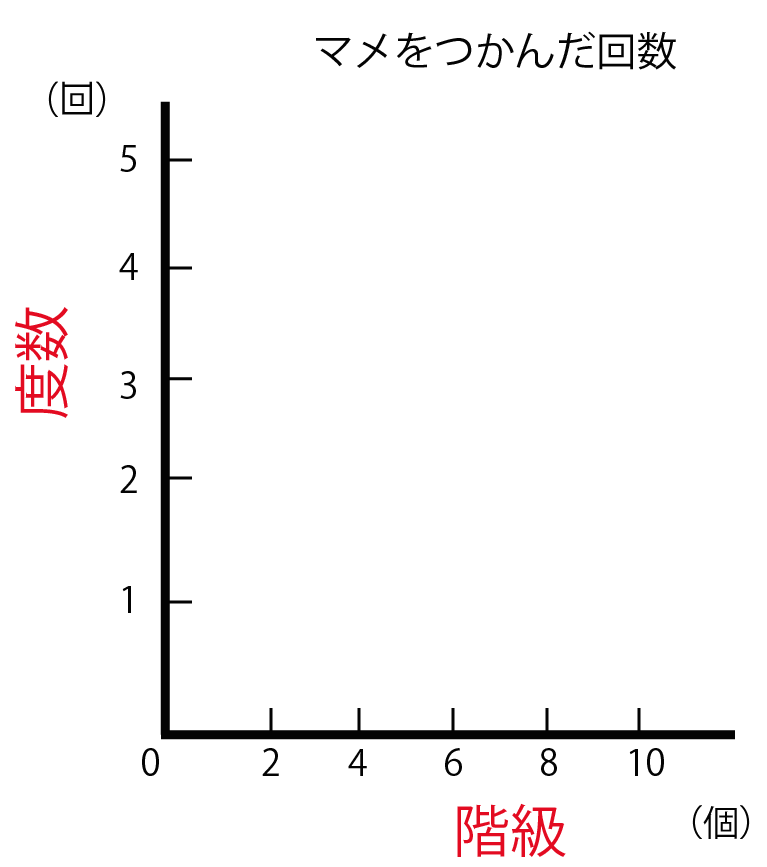
これでヒストグラムの目盛りは完ぺきですね!!^^
次はヒストグラムに「度数」の値をいれていきましょう!
それぞれの階級の度数の点をうっていくだけでいいんです。さっきのヒストグラムは、
こうなりますね!
いよいよ最後のステップ。先ほどプロットした点が上の辺になるように長方形をかいていきます。
棒グラフをヒストグラムに書き込んだら必ず「点」を削除してくださいねー!
これでヒストグラムの完成です!書き方はぜんぜんむずかしくないですよね!?。
資料の活用で最初につまずく点が「ヒストグラム」。
これさえクリアできれば中学1年生の数学を攻略したも同然です!
次回は度数分布多角形について解説しまーす。
それじゃねー!
Kenny
<<関連記事>>
こんにちは、Kennyです。
「資料の活用」に「階級」ということばが登場します。
これはカンタンに言ってしまうと、
データを整理するためのグループのこと
です。わかりずらいので例をみてみましょう。
たとえば、ぼくが「マメをつかむゲーム」に参加したとしますよ??
左の皿から右の皿へマメをうつすゲーム。
10回トライしてみました。制限時間は1分間。
すると、以下のような結果が得られたのです。

この表から、
「ぼく」が何個のマメをつかめる可能性が高いか、
を調べたいとき。
そんなときに階級が登場します。
1個つかんだときはo回、
2個つかんだときは1回、
3個つかんだときは0回、
・・・・・・・
と数えてたら日がくれちゃいますよね?? 表もこんなにデカくなっちゃいます。

マメをつかめた回数を階級でわけてあげましょう。マメの数を「0~2」、「2~4」というように2個きざみで結果をグループわけしてあげます。すると、

表に記入する数字がへりましたよね??
データの量をグループ分けして減らしちゃう!
これが「階級」の役割ですね。
「0~2」や「2~4」というグループ分けした区間のことを「階級」というんです。
このデータから、
「ぼく」は「4以上6未満」個のマメをつかめる可能性が高いことがいえます。
そして、この表でいう「回数」を「度数」と呼んでいます。つまり、ある階級に属する事象がおこった回数のことですね。
ついでに、こんな感じで
階級と度数を整理した表を「度数分布表」っていいます。
資料と活用に登場する「用語」と「意味」はしっかり押さえておきましょう!
これで階級の解説はおわりです。
次回は階級に関する2つの注意点についての記事を書きますね。
それじゃねー!
Ken
<<関連記事>>
こんにちは、Kennyです。中学1年生の数学「資料の活用」を攻略法を解説しますよ!
「資料の活用」という単元はひとことで言うと、
「統計学」の基礎
です。
多くのデータからある新しいことを知ることができる学問。
これが統計学です。

「資料の活用」を攻略するコツを3つ紹介しますよ。
「資料の活用」をクリアするコツは以下の3つです。
「資料の活用」には専門用語がたくさん登場します。ことばの意味はむずかしくありません。が、数学用語の数が多いです。たとえば、
ヒストグラムとか、
相対度数とか、

メジアンとか、
です。耳がいたくなってきますよね。??
マイ勉では一語一語ていねいに解説していきますよ。 テスト前にがんばって暗記していきましょう!
資料の活用では「小数の計算」をたくさんします。
小数の計算ミスを少なくしましょう!
資料の活用での「小数の計算」は基本的なものばかり。たとえば、
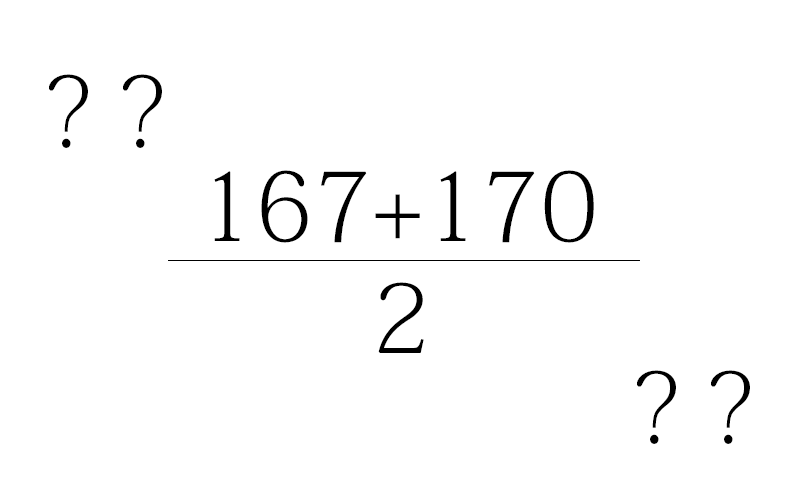
といった感じ。落ち着けばミスを防げるはずです!。
中学1年生の「資料の活用」では表とグラフを描く問題が出題されます。
だから、
という2つのスキルが必須なんです。たとえば、
こんな度数分布表をつくったり、
表をもとに次のようなグラフ(ヒストグラム)を作ったりします。
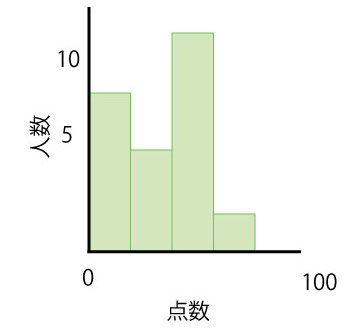
グラフが描ければクラスの人気者まちがいなしです。
「資料の活用」を攻略するコツは、
の3でしたね??
「資料の活用」で先生やクラスメイトを驚かせましょう!
それじゃねー!
Ken
<<関連記事>>
こんにちは、この記事を書いているKennyです。銭湯で汗を流したい気分です。
中学1年生で勉強する「文字式」もいよいよ終わっちゃいます。文字式というヤッカイな単元が終わってせいせいしますね?? 今日で文字式の記事は終了です。

だがしかし、今日勉強する「関係を表す式」は今までの文字式とはひと味もふた味も異なります。
今までは、
文字を使って「計算」を表していました。たとえば、3x+yといった感じ。もしxとyに数字を入れたら「式の値」を求めることができましたね??
今日、この文字式の最後の単元では、
文字を使って「関係を表す式」をつくってみます。
つまり、単なる「計算」ではなくて「関係を表す式」だということ。
この点に注意してくださいね。
中学1年の数学で勉強する「関係を表す式」には以下の2種類存在しています。
「関係を表す式」とは「右と左の式」の値の関係を表わしている式です。「関係を表す式」で左側の式のことを「左辺(さへん)」といい、右側の式のことを「右辺(うへん)」と呼んでいます。
左側にある式が左辺、右のやつが右辺。わかりやすいですね!
そんで、左辺と右辺の間には「等号」か「不等号」が挟まれているんです。「等式」の場合は「等号=」が、「不等式」のときは「不等号 <>」が挟まっています。

2つの「関係を表す式」である「等式」と「不等式」について詳しくみていきましょう。
等式とは、
2つの数量が等しいこと示した式
です。「左の計算式(左辺)」と「右の計算式(右辺)」の値が等しいということを意味します。等式では左辺と右辺のあいだに「等号=」を間に挟みます。たとえば、
6x-8と、
4y+3という2つの文字式が等しいとします。この関係をを等式で表現したとしましょう。すると、この等式は等号「=」をはさんで、
6x-8 = 4y+3
となります。左辺と右辺の2つの計算式で「等号=」をサンドイッチするだけです。リアルな世界でサンドイッチをこねるよりカンタンですよね。
不等式とは、
等しくない、2つの式の大小関係を表した式
です。等式のときと異なり、2つの計算式は等しくありません。左辺が大きくなることもあれば、右辺が大きくなることもあります。
たとえば先ほどの例を再利用して、
6x-8のほうが、
4y+3よりも大きいことを表した不等式をつくってみましょう。「>」という不等号を用いれば、
6x-8 > 4y+3
という不等式が誕生します。みごとに左辺と右辺の文字式で「>」という不等号をサンドイッチしています。逆に、4y+3のほうが大きい場合は「<」という逆の不等号を使ってやりましょう。
不等式でつかえる不等号には次の4種類あります。
えっ。「≦」と「<」の違いがわからないですって?? そんな中学生のために「不等号の意味」についての記事を書いてみました。よかったら参考にしてくださいね。
中学1年生の数学で押さえるべき「関係を表す式」は、
の2種類だけ。上で解説した2つの意味を覚えれば大丈夫。どんな文字式の関係だって表すことができます。「関係を表す式」は次の章で勉強する「方程式」で大活躍します。今のうちに等式や不等式の使い方をマスターしておきましょう。
それじゃーね!
Kenny
こんにちは、2日連続でスパゲッティーを食べたKennyだよ。
文字式の分数の問題に苦手意識持ってないかな!? そうそう、文字式の分数問題。
たとえば、
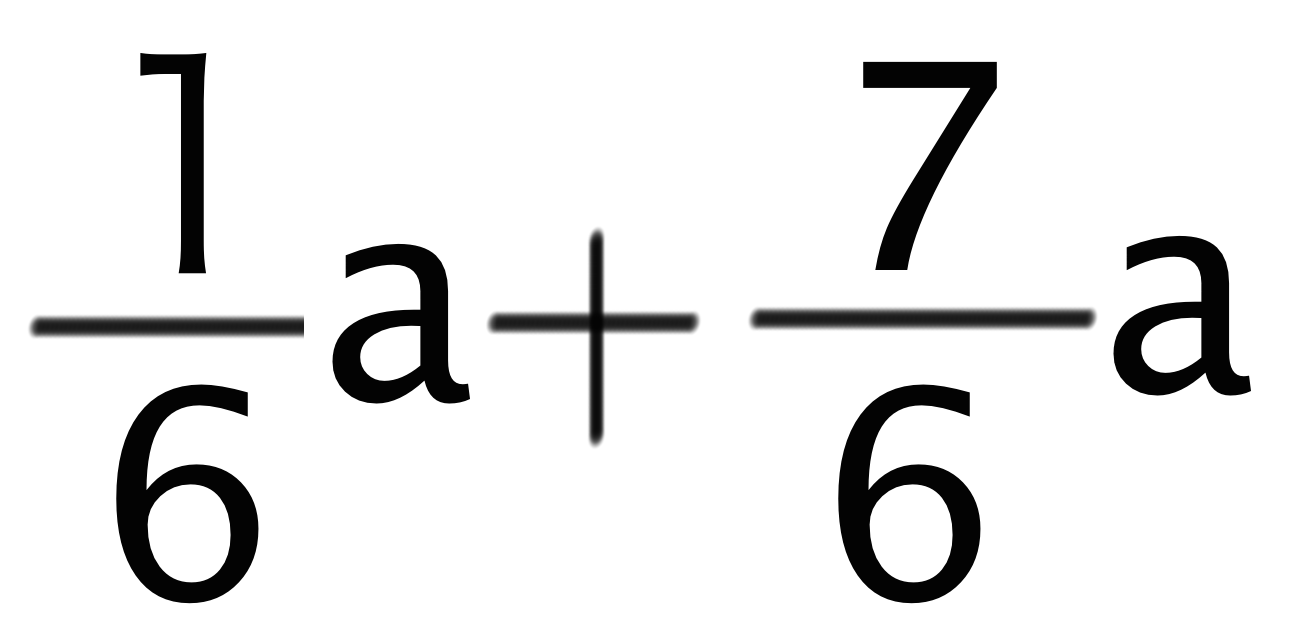
とか、
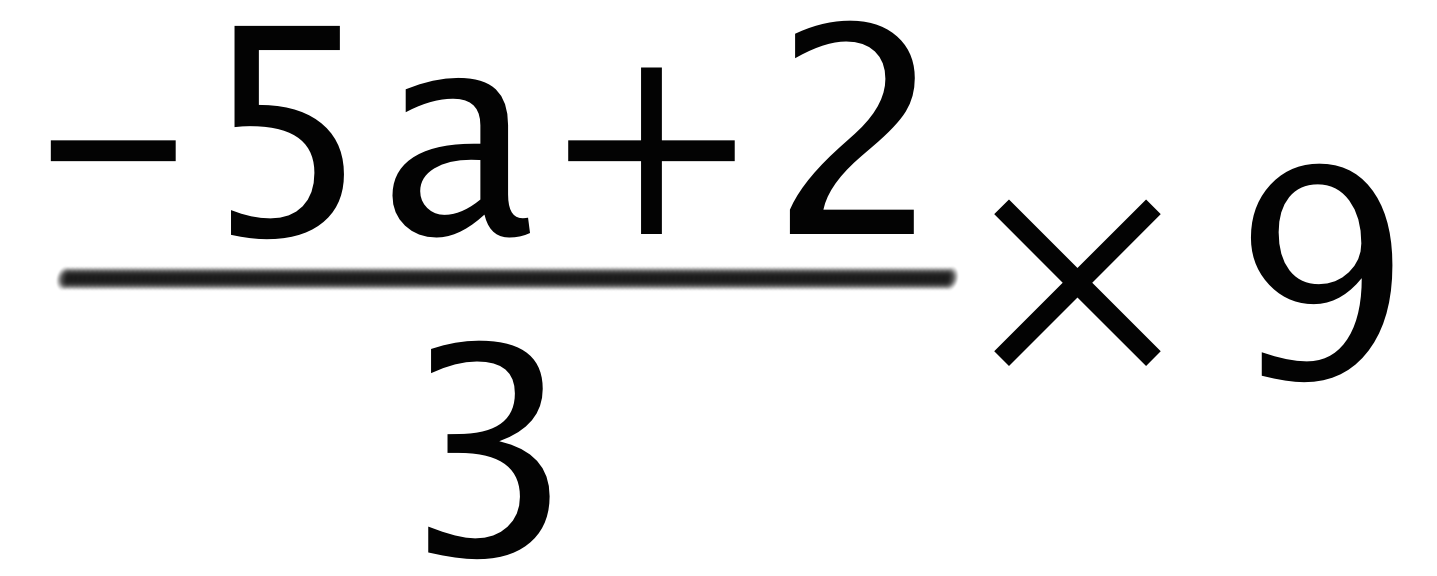
とか。こんな感じの分数の文字式の計算ってじつは4つのパターンしかないんだ。
えっ。文字式の分数問題が苦手だって?!?
今日は苦手を克服するためにもKennyが「文字式の分数問題」のパターンを4つ紹介するね。そんでもって、とっておきの解き方も紹介しちゃうよ。中間テストが近づいた時に参考にしてもらいたいね。
それじゃさっそく4つの文字式の分数問題のパターンを紹介してみるね。
1つ目のパターンは分数と分数の計算。
これは文字式の分数の計算の中で一番カンタンなパターンだからしっかり覚えておこう。
たとえば、という分数の文字式をみてみよう。
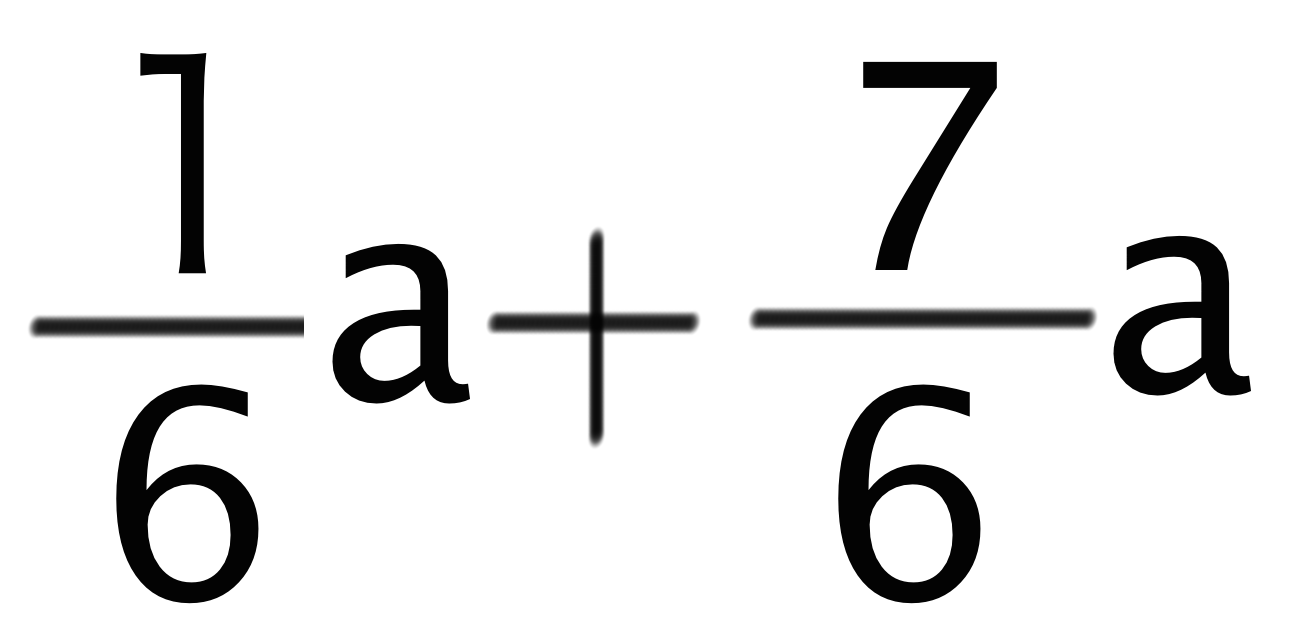
この文字式では2つの項の分母が「6」で等しいよね?? こういうときは、
分子をそのまま足してあげちゃえばいいんだ。
2つの項の分子はそれぞれ「1」と「7」だから「1+7=8」だよね?? よって、この分数の文字式の計算問題は、
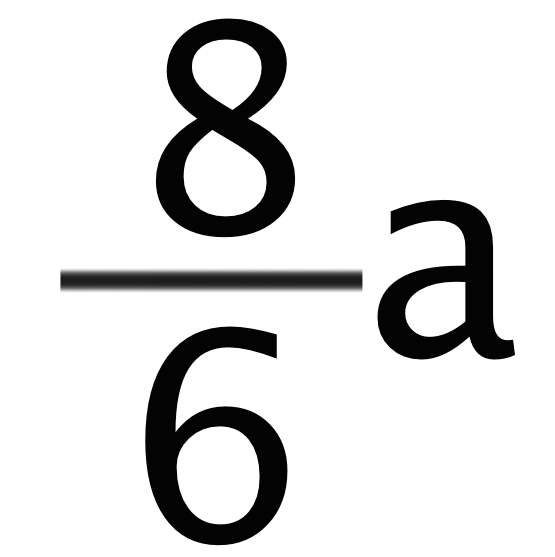
という答えになるね。ただし、
分数の文字式の計算では必ず「約分できるかどか」を確認するようにしよう。この文字式の答えでいえば分母の「6」と分子の「8」はお互い「2」で割れるよね?? っていうことは約分できるってこと。よってこの分数の文字式の計算の答えは、
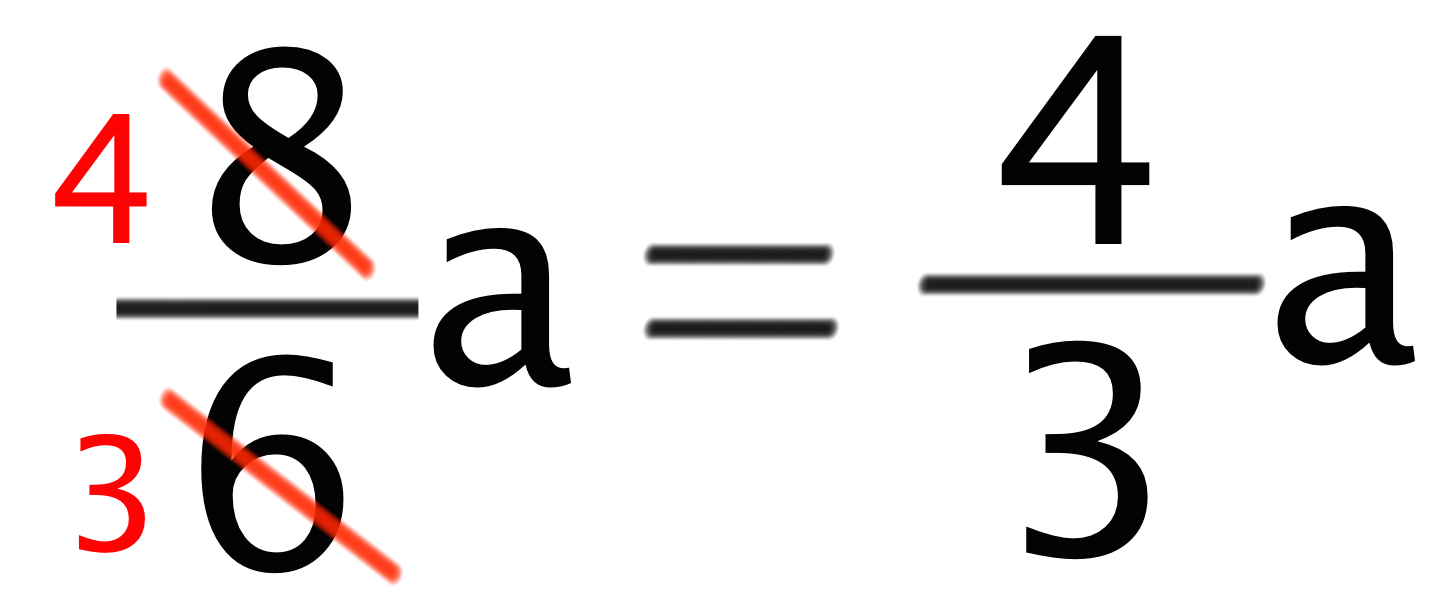
になるよ。約分をくれぐれも忘れずにね!!
2つ目のパターンは、分母がちがう分数を足し合わせる文字式だ。
このパターンでは、
分母を通分する
というステップが入るからちょっとややこしいね。例題をみてみよう。
たとえば、という分数の文字式。
分母が違う文字式の分数足し算では、まず通分しなきゃいけないんだ。通分って小学校で習ったよね??
分母の「5」と「3」の最小公倍数を探して、そいつを新しい分母にしちゃえばいいんだよ。
この場合、「5」と「3」の最小公倍数は「15」だから、2つの項の分母を15にそろえちゃおう。すると、
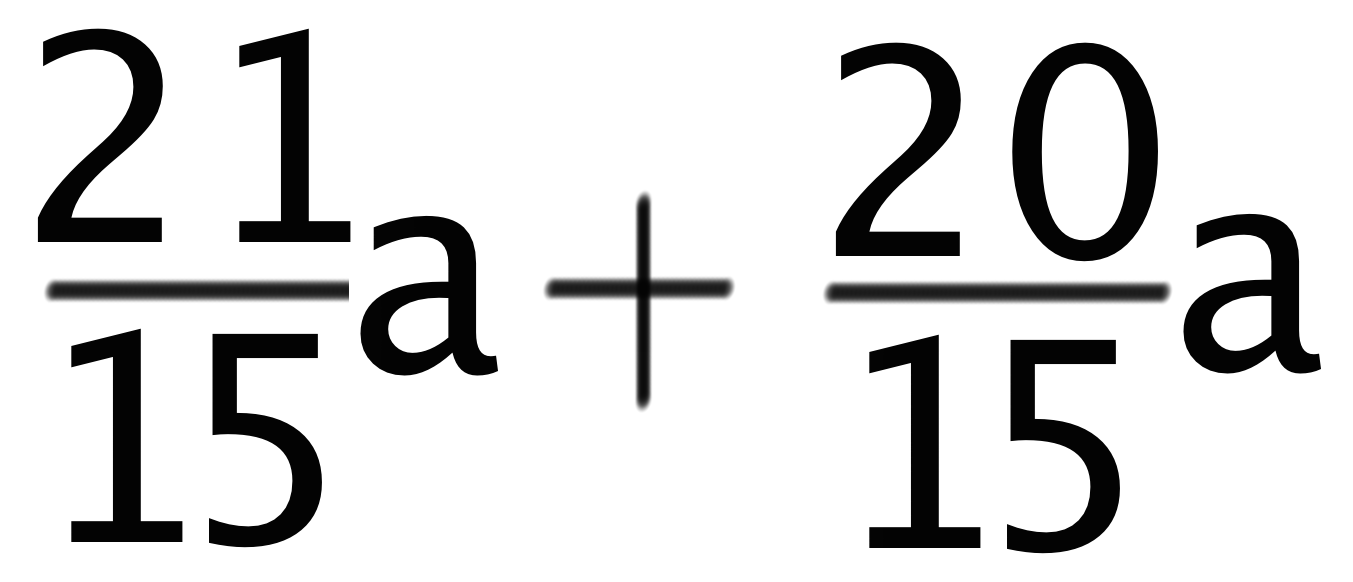
こうなるね。分母が等しくなったから、2つの文字式の分数を足しちゃおう。
すると、という計算の答えになるね。通分の計算でくれぐれも間違えないようにしよう。
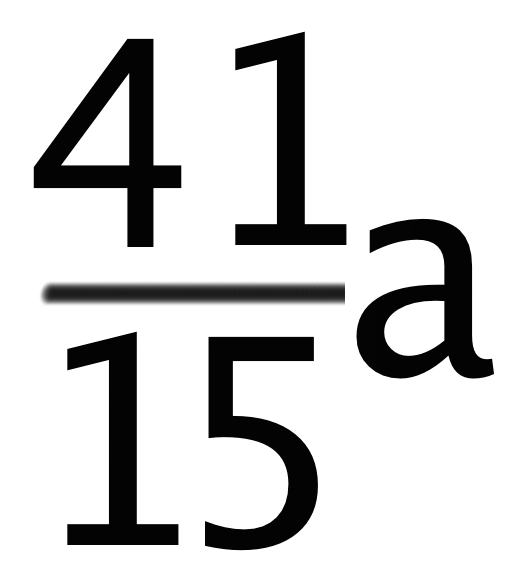
3つ目のパターンは分数と分数以外の文字の足し算だよ。たとえば、
という文字式を例にとって説明しよう。
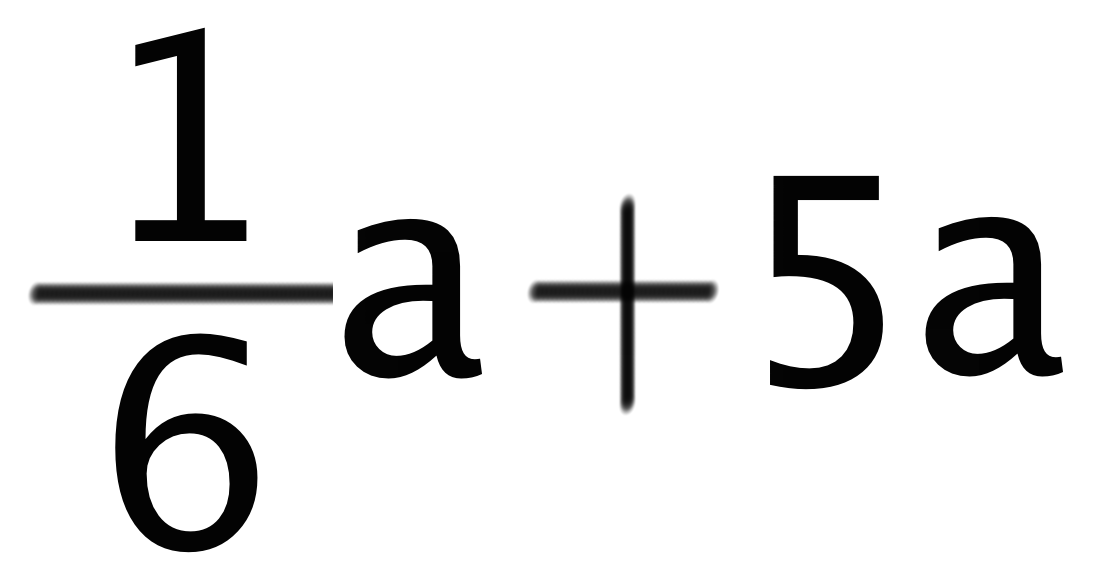
こういうときは、分数+分数の形に直してから計算するようにしよう。さっきのでいえば、5aという分数じゃない項を分数にしてやると、
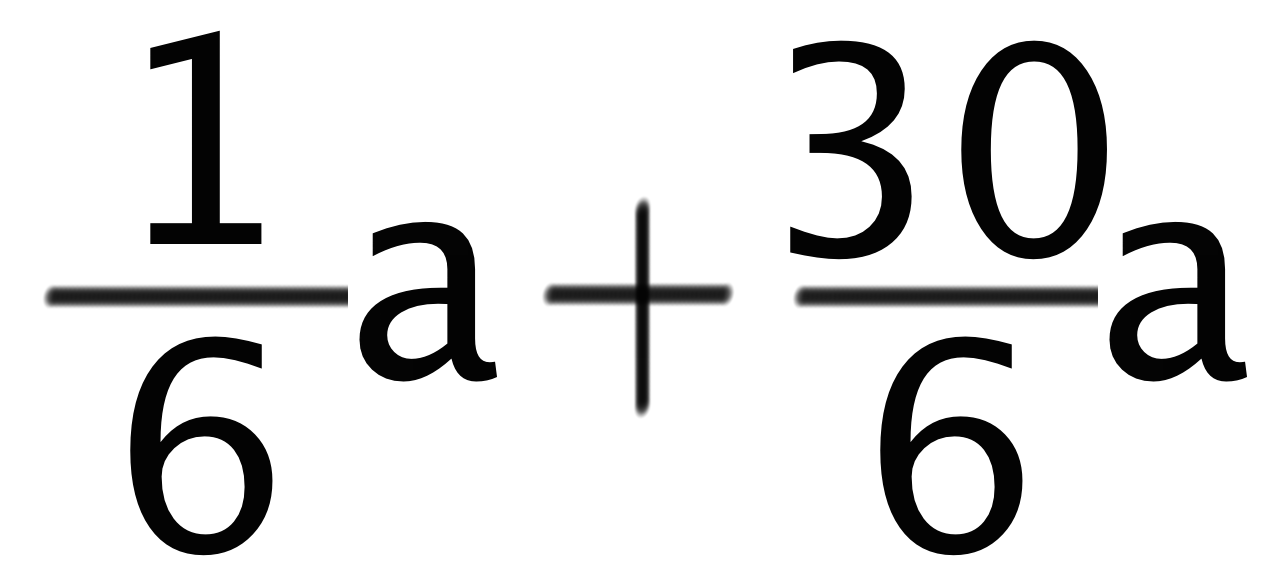
ってなるよね?? あとは分子を足してあげるだけ。よって、答えは になるよ。
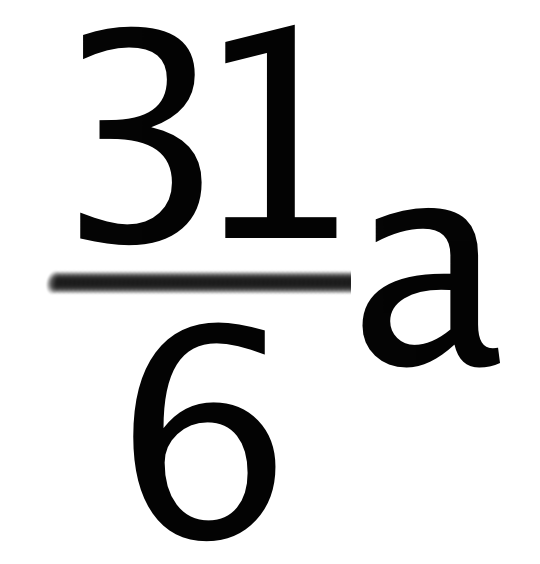
最後のパターンは分数の文字式に「整数」を掛けたり割ったりした問題。たとえば、
という分数の文字式をみてみよう。
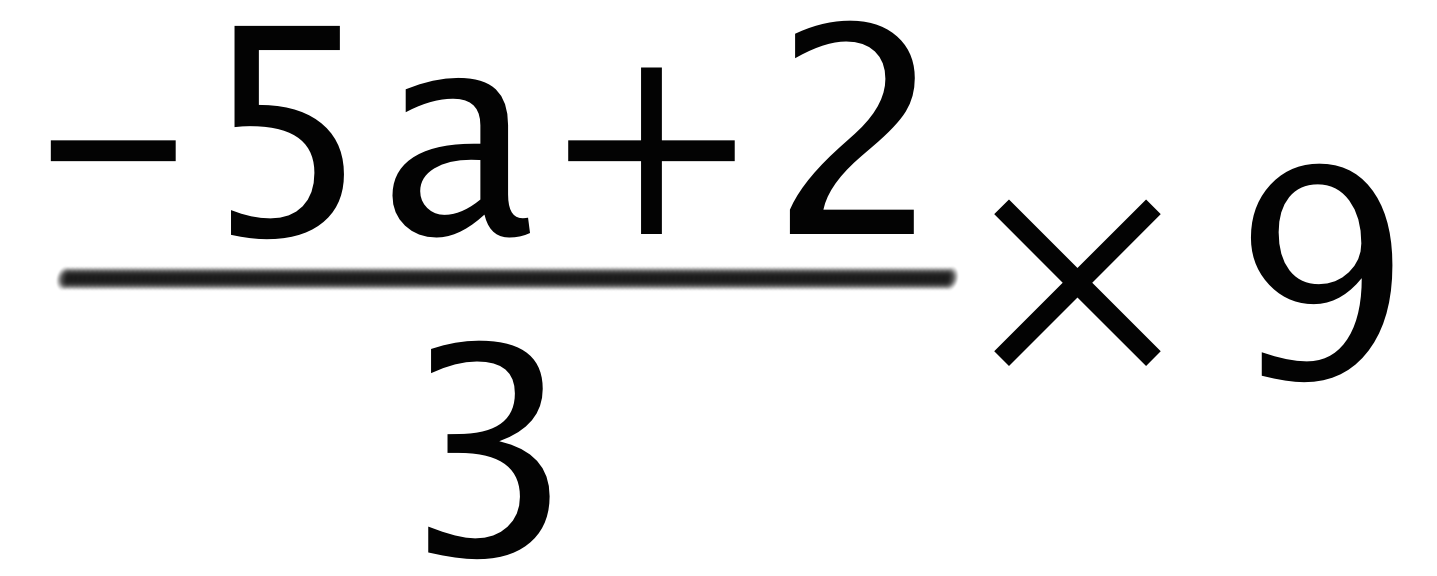
このタイプの文字式問題は次の2つのステップで攻略しちゃおう。
さっきの例題でいえば、まずはこんな感じで分数を分母と分子に分解しちゃうんだ。
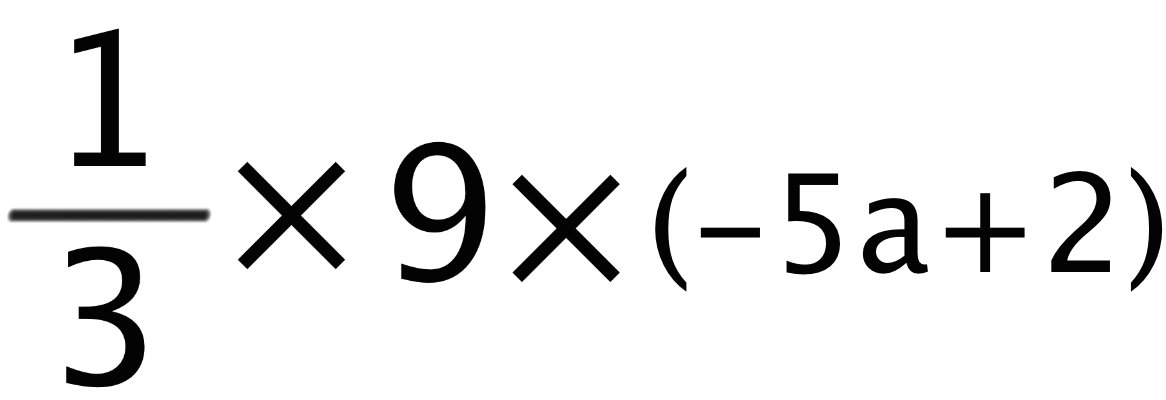
そっから、分母だけの分数と整数を掛けてみると、
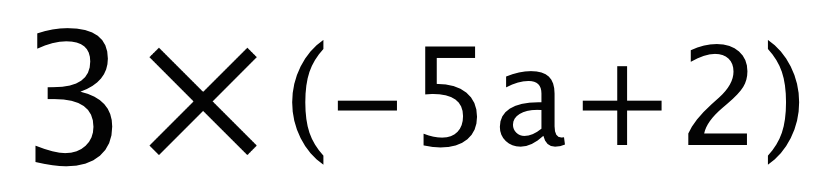
ってなるんだ。これを分配法則をつかって解いてあげると、っていう答えになるね。
 このタイプの計算で注意することは、
このタイプの計算で注意することは、
分配法則を間違えずに計算し終えることだ。カッコ内の1つの項にしか掛けなていないミスがあるからね。十分に気をつけよう!
ここまで分数の文字式の計算問題を解いてきたね。どうだったかな??
学校のテストの分数の文字式の問題はゼッタイに4つのパターンに当てはまるよ。だから、テスト前にこの記事を読んじゃえばゼッタイに大丈夫。復習を忘れずに。
それじゃねー
Kenny
文字式の表し方をしっかり勉強しましたね??
次はいよいよ文字式の計算問題に挑んで行きます。「文字式の計算問題」と聞くと難しく聞こえますよね??
す、数字だけの計算はもはや通じない。ど、どうしよう、、中間テストが迫ってきている・・・・・

そんな危機的な中学生の方のために、
【中1数学】文字式の計算問題の解き方に関する3つのコツ
という記事を書きました。
文字式の計算問題の解き方をまったく知らない?? そんな中学生でも1秒で問題をとける方法です。中学校のテストで死にそうになってるときに参考にしてみてください。
さっそく「文字式の計算問題の解き方」のコツを紹介していきます。
文字式の計算問題の解き方は、以下の原則が大前提になっています。それは、
掛け算 → 足し算
です。
これは正負の四則演算でも同じでしたね。文字式でもこの原則は一緒!!
「掛け算」を計算してから「足し算」を片付けるようにしましょう。
それでは、文字式の計算問題を瞬殺するための3つのステップをみていきます。
文字式の計算では最初に「掛け算記号×」と「割り算記号÷」を消し去っちゃいましょう。
文字式の表し方で、
文字式では「×」と「÷」の演算記号を省略するぜ!
ということを勉強しましたね?? ところが、文字式の計算問題の中には「×」と「÷」が省略されていない文字式もあります。たとえば、
という文字式の計算問題。こういうときは「÷」記号を消し去ることが大切。つまり、割り算の計算をしてしまうということです。
「×」や「÷」の計算記号を残したままでは文字式の計算問題を解いたことになりません。テストで100点をとるためには「×」と「÷」を消去する文字式の解き方を覚えておきましょう。
次に、文字式の計算問題の「カッコ()」を消しちゃいましょう!
えっ。文字式の問題でカッコ()のはずし方がわからないですって!?? あ、そういうときは、
分配法則
を使えばいいんです。詳しくは【中学数学】分配法則のチョー便利な1つの使い方を参考にしてくださいね。分配法則とはカンタンに言ってしまえば、「カッコのをはずしたる」ということです。
文字式の計算問題の例をみてみましょう。
たとえば、
という文字式の計算問題があったとしましょう。この文字式には「3」という数字がカッコ()の前についています。分配法則をつかってカッコ()をはずしちゃいましょう!
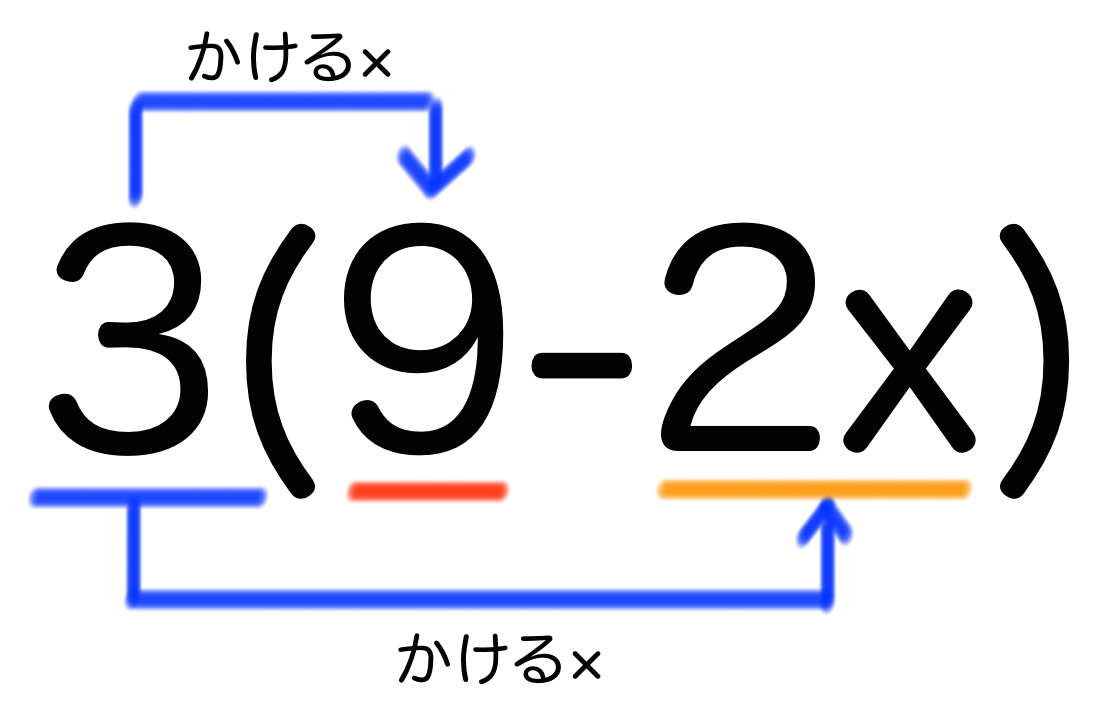
すると、
となります。
カッコ()がついている文字式の問題は分配法則でスッキリしちゃいましょう!
ここで注意することは、
カッコの外の数字がマイナスの計算問題
です。の場合、
とするのは間違いです。なぜなら、
には
でなく
をかけてしまってるからです。
正しい答えはカッコ内の2つの項に「-3」を等しく掛けたです。カッコをはずすときにはマイナスの符号に注意しましょう!
いよいよ文字式の計算の最後のステップです。
「掛け算×」も「割り算÷」もなし!
「カッコ()」もなし!!
これだけでは文字式の計算は終わりません。そのあとに、
同じ文字の項をまとめる!
という作業が残っています。これはいったいどういうことなんでしょうか??? 文字式の例題で確認してみましょう。
たとえば、4(2x-5)-3(9-2x)という文字式の計算問題があったとします。
さっきとりあげたステップのうちの2つ目の「カッコ()をはずす」という解き方を適用すると、
4(2x-5)-3(9-2x)=8x-20-27+6x
となります。ここで最後のステップ「同じ文字同士をまとめる!」という計算をしてみましょう。この式には「x」と「数字」という2種類の文字が存在します。これらをまとめてやると、
8x-20-27+6x=14x-47となります。
同じ種類の文字・数字をまとめてようやく「文字式の計算問題を瞬殺した」と胸を張れます。
最後まで気を抜かないで文字式を計算してやりましょう!!
以上の3つのステップを踏めば、文字式の計算問題をたぶんおそらく3秒ぐらいで瞬殺できるはずです!!
文字式の計算に時間がかかりすぎるという悩みをかかえている中学生は参考にしてみくださいね!
それでは、また今度です。
Ken