こんにちは!皮膚科にかかっているKenだよ!
中学1年生で「比と比例式」を勉強しなくちゃなんないよね?! 正直だるいし、方程式でおなかいっぱいだ。
だけど、この「比と比例式」は基本さえわかっちゃえばむちゃくちゃ楽勝なんだ。
がんばれば期末テストの得点源になったりする。
だから、今日は「比と比例式」に登場する、
「比の値」
というものは何か??ということをわかりやすく振り返ってみよう。基本さえ押さえちまえば方程式の解き方を勉強するより楽勝だよ!
「比の値」を次の3つのステップで勉強していこう!!
「比の値」を理解するためには、まず、
算数で習った「比」を復習しなきゃならないんだ。
これは「比と比例式」を攻略するために一番大切なこと。しっかりと「比」の意味を押さえておこう。
「比」とはWikipediaによると、
2つ(または3つ以上)の数の関係を表したもの
って書いてある。つまり、2つ以上の数のどっちがどれぐらい大きいのか、ということを表している便利なアイテムなんだ。
たとえば、ぼくのお小遣いが1000円。きみのお小遣いが10000円だとする。かなりもらってるね。 うらやましいよ。
このとき、「きみのお小遣い」は「ぼくのお小遣い」の10倍だね??
このお小遣いの格差を比で表してあげるとこうなる↓↓
「:コロン」をはさむだけで2つの数量を比較できるんだ。おこづかいでもテストの点数でも1500mのタイムでもなんだってありさ。
これが小学校の算数でならった「比」だよ。しっかりと押さえておこう。
次に押さえておきたいのは「比の項」だ。
さっきの「比」という用語さえ理解してればちょちょいのちょいさ。たとえばさっきの例でいえば、
1 : 10の「1」を「前の項」、「10」を「後ろの項」とよんでいるんだ。そして、両方には「比の項」っていう名前がついてる。しっかり押さえておこう。
やっとこの記事のテーマである「比の値」にたどりついたね!
じつは「比の値」はさっきまで勉強してきた「比の項」を理解してれば楽勝なんだ。
比の値とはずばり、
(前の項)÷(後ろの項)なんだ。
だからさっきの「おこづかいの比」の例でいえば、
10分の1が「比の値」になるんだ。
前の項と後ろの項の順番さえ間違えなきゃ大丈夫だね!。
ここまで勉強してきた「比の値」はよくわかったかな??
比の値をしっかりおさえて次の比例式に備えちゃおう!
そんじゃねー!!
Ken
こんにちは!この記事を書いているKenだよ。岩盤浴にハマってるんだ。
前回は「分数がふくまれる」方程式の解き方をみっちり勉強してきたよね?? これさえマスターしてまえば中1数学の方程式をクリアしたも同然さ。
ただ、分数をふくむ方程式と同時に気をつけてほしいのが、
小数をふくむ一次方程式の解き方
なんだ。
分数よりヤッカイじゃないけれど、気をつけないと間違ってしまうことが多い。だから今日は、
小数をふくむ一次方程式の解き方で気をつけるべきことを1つだけ紹介するね。
小数がはいった方程式の解き方では、
小数を消し去る
ということを初めにやっちゃえばいいんだ。
これがどういうことか説明していこう。たとえば、次のような小数をふくむ一次方程式があったとしよう。
0.3x = 0.05x + 1
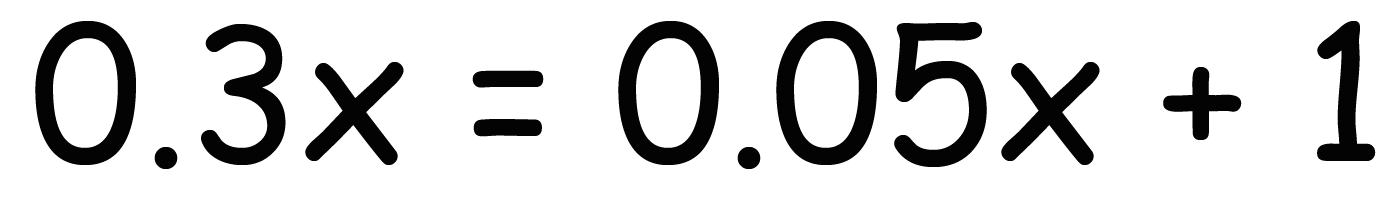
小数を消し去るためには、
一番小さい小数の位がなくなるような数を両辺にかけてやればいいんだ。
えっ。何をかけたらいいのかわからないって??
ゆっくり考えてみよう。
小数第一位の数である「0.3」には何をかけたら小数じゃなくなる??
そう、10だ。
じゃあ、小数第二位である「0.03」は??
そう、100だ。
っというように、「10を小数の位数分乗したやつ」を方程式の両辺にかけてやればいいんだ。
だから、
0.3 x = 0.05x +1
という方程式では「0.05」が一番小さい小数の項だよね?? こいつはちなみに小数第二位だ。だって、小数点より右に2つの数字が並んでるからね。
だから、
10の二乗、つまり100を方程式の両辺にかけてやればいいんだ。
30x = 5x + 100
こんな感じでスッキリした方程式に早変わりさ。
ただ、右側に注意してくれ。
ぜんぶの項に100をかけてあげないと等式が成り立たないんだ。この場合だと、「0.05x」と「1」だね。ゆっくりと解けば間違わないはずだ!
こいつを「基本的な1次方程式の解き方」を使って解いてやれば、
x = 4
という解が得られる。これで小数の方程式も楽勝さ!!
小数をふくむ1次方程式の解き方はどうだったかな??
分数の方程式よりもカンタンだったよね?? この調子で中1数学ででてくる方程式の解き方をじゃんじゃんマスターしてっちゃおう!!
そんじゃねー!
Ken
こんにちは!1日に映画を5本みたKenだよー!
中1数学で勉強する方程式はまだ可愛い方だよ。だって、文字が1つしか登場しないからね。このタイプのものは一次方程式だとか、xの方程式とかと呼ばれている。
この解き方は前回の「【中学数学】1次方程式(xの方程式)の解き方の3つの手順〜基礎編〜」で勉強したからもう大丈夫だよね??

じつは方程式でつまずく人が多いと言われているのは、
分数が含まれた方程式の解き方
を理解することなんだ。分数が含まれるとちょっと厄介。いままで楽勝に見えていた方程式がむずかしくみえちゃう。これは勉強する側としてはとても嫌。。
だから、今日は中1数学の方程式の解き方でつまずかないためにも、
分数がふくまれる1次方程式の解き方
を2つのステップで振り返ってみよう。
前回勉強したチョー基礎的な方程式の解き方を応用できるまでに、
分数の方程式ではやることが2つあるんだ。
たった2つだけ。
これさえやっちゃえばいつも通り方程式を解くだけでいいんだ。カンタンそうでしょ??
分数の方程式の解き方を説明するために、今日は、
(2x + 5)/3 = (x-4)/4
という分数入りの方程式の解き方をみていくよ!
まず最初に「分母を払う」というワザをつかって分数の方程式をシンプルにしちゃおう。
「分母を払う」とは、
分母をなくしちゃうこと。つまり、分数を方程式から消し去ろう!ということなんだ。
そのためには具体的に、
左と右の分数の分母の「公倍数」をかけてあげればいいんだ。
えっ。公倍数がよくわからない?? Wikipediaによると公倍数とは、
2つ以上の正の整数の、それらに共通する倍数のことをいう。
とあるよ。つまり、2つ以上の数字をそれぞれ何倍かずつしてやれば同じ数になる。このとき、その「同じ数になる数字のこと」を公倍数っていうんだ。
たとえば、「3」と「4」の公倍数は12。だって、「3」を4倍したら「12」になるし、「4」を3倍しても「12」になるからね。
だからさっきの例題の、
には、まず分母の「3」と「4」の公倍数12を方程式の両辺にかけてあげるんだ。等式を成り立たせるために、かならず両方に同じ数をかけてね!
そうすると、
こうなるよね??
そんで、左の分母3と、右の分母4が12によって消されちゃうので、
こうなる。
ここで注意してほしいのは分子をきっちり()でくくってやること。分母を払うためにかけた数字の残骸(ここでは赤い数字の4と3)で分子を()でくくるのさ。
これを忘れると計算結果が異なってくるので注意してね。
あ、分母の公倍数がよくわからん!
というときは分母の数をそれぞれゆっくりかけてみてもいいよ。たとえば、この例でいえばとりあえず「3」を両辺にかける。そんで、次に残った分母の「4」をかける。
これでもおk!
さて、次が一番間違いの多いところだよ。分母を払って安心しちゃう奴が多いんだ。
分母を払ったときに残った残骸で分子を包んだね???
そしたら、その()を分配法則をつかってはずしてみよう。
()の外の数字を中の数字すべてにかけるのを忘れずにね!
分配法則をつかって()をはずしてやると、
8x + 20 = 3x -12
になるよね??
この方程式のカタチはチョー基本形。だから「【中学数学】1次方程式(xの方程式)の解き方の3つの手順〜基礎編〜」で紹介した解き方を使ってやればすぐ解けるんだ。
xと数字の項を移行して分離させ、そしてxを裸にしてやると、
x = -32/5
分数をつかった方程式でやっかいになる解き方は上の2つだけでいいんだ。あとは基本的な方程式の解き方と同じ。ゆっくりやればとけそうだね。
ここまで勉強してきた分数の方程式の解き方はどうだったかな?? 分数の方程式とかむずかしそうに聞こえるけど、ちょっと手順を付け加えてやればちょちょいのちょいさ。
計算ミスをしないようにゆっくり解いてみよう!!
そんじゃねー!!
Ken
こんにちは!イボコロリを使ってみたKenだよ。
中1数学でむずかしいと言われているのは「方程式」。中1で勉強するのは「1次方程式」とよばれているものだ。なにせ、文字が1つしか含まれていないからね。
ちまたでは「xの方程式」と呼ばれているらしい。

今日は「一次方程式」の解き方の手順を3つにわけて紹介するね。
でも、中1で勉強する1次方程式にも「むずかしいもの」と「簡単なもの」があるんだ。
まず手始めということで、
今日はxの方程式の解き方の基礎的な手順を書いてみた。よかったら参考にしてみてね。
それでは簡単な1次方程式(xの方程式)の解き方を振り返ってみよう。xの方程式の具体例として、
7x-2 = 5x +10
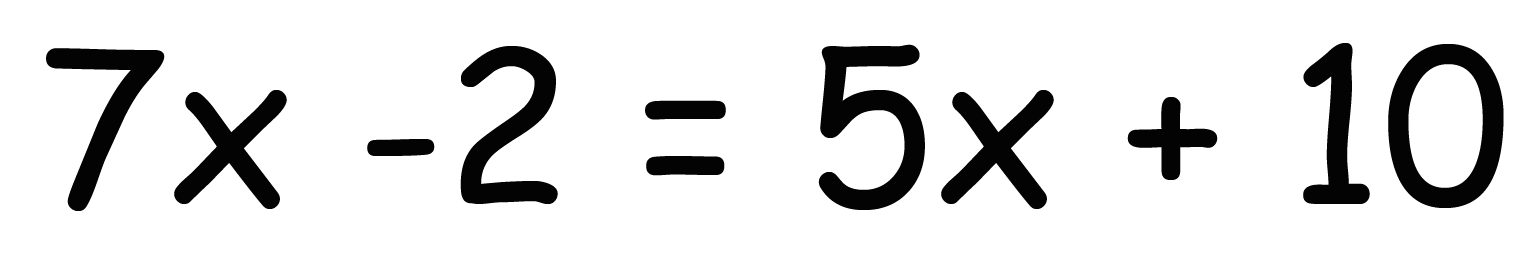
という方程式をつかって考えてみるね。
まず一次方程式(xの方程式)でやるべきことは、
等式の左に文字xの項をよせること
だ。この方程式でいえば、
「7x」と「5x」が「xの項」だよね?? だって、項の中にxが含まれているからね。
7xはもともと左にあるから、5xをがんばって左側に持ってこよう。
項を移動させるときは前回ならった「移項」というワザを使うんだ。超シンプルにいうと、移項とは「逆側に項を移すときに符号を変える」というもの。
だから、5xにマイナスの符号をつけて、コイツを左に持ってくるんだ。
これで方程式の解き方の第一ステップは終了!
次はx以外の項。つまり、数字の項を右側によせちゃおう!!
さっきの例でいえば、「-2」と「10」が数字の項だね。
右への寄せ方は手順1と同じだよ。
そう。移項というワザを使ってやるんだ。符号を変えながら数字の「-2」という項を右へ移してやるとこうなる!
左に文字、右に数字を寄せたね??
次はその寄せた項同士で計算してもっとシンプルな形に変えてやればいんだ。足し算や引き算であることが多い。
さっきの例の「左」と「右」の計算をしてカンタンな式にしてやればこうなる↓↓
2x = 12
これは俗にいう、
ax = b のカタチ
というやつさ。ここまでくれば方程式は解けたも同然。あと一歩だから踏ん張ってみよう!!
最後はxを裸にしてあげるんだ。つまり、
x = ~~~~
というように、xの項の係数をかならず1にしてあげる。これを巷では「xを裸にする」といわれているんだ。
「解き方3」から「解き方4」に移行するためには、
xの係数で左と右の式を割ってあげればいい。
たとえばさっきの例でいえば、
左のxの項の係数は2だよね。だって、xの前に2がついているから。
だから左と右の両辺を「2」で割ってみよう。するとこうなって、
最終的にこうなる↓↓
つまり、
この方程式の解は「6」ということだね! xの値が方程式の解だから当然だよね?? これで中学1年生で勉強する「一次方程式」をマスターしたも同然だ。
以上で一次方程式の解き方は終了だよ。
あくまでもこれは超基礎的な方程式の解き方。だからこれだけじゃ解けない方程式もあるよ。
だから次回は、中1数学の方程式の解き方の応用編について語っていくよ。お楽しみにー!!
そんじゃねー!!
Ken
こんちゃー!イヌの散歩にはまってるKenだよー!
中学1年で勉強する「方程式」。ここで一番の疑問って、
なぜ移項することができるのか!??
ってことだよね。今日は移項とは何か?? という基礎的なことを振り返りながら「移項ができる理由」を振り返ってみよう!!
~もくじ~
中1で勉強する「1次方程式」をとくために便利な「移項」というワザ。いったいコイツは何者なんだろうか。
まずは移項の正体をあばいちゃおう。
数学の教科書をみてみると「移項」って次のように定義されてるんだ。
等式では、一方の辺の項を、符号を変えて、他方の辺に移すことができます。このことを移項するといいます。
この移項を図をみながらゆっくりみよう。
「一方の辺の項」
を、
符号を変えて、
他方の辺に移す。
これが移項なんだ。
つまり、
等式では、
項を左から右に移動させてもいいし、右から左に移動してもいいんだ。ただし、符号は変えてね。
これが方程式で重要となる「移項」の意味なんだ。
しっかり頭にぶちこんでおくれ!
それじゃあ、なんで移項って超能力ができるんだろうか!? 左から右へ符号を変えるだけで項が運べるなんてエスパータイプのポケモンみたいだよね???
じつは移項って「等式の性質」を使っているんだ。
※ 等式の性質にイマイチピンとこないときはこの「等式の性質の記事」で復習してくれ。
さっきの例では等式の性質の1つである、
「両辺から同じ数をひいても等式は成り立つよっ」
っていうものを使っているよ。
ためしに、
5x + 17 = 32 という等式の左と右から「17という数」をひいてみよう!
すると、
こうなる。
そんで、左の17-17がゼロになるよね!?
だから、
17という項があたかも「移項」したように見えるわけ。
移項って左から右に移すときに符号を変えるだけ。
だから、ものすごく簡単に感覚的にできちゃうんだ。だけれども、一番大切なのは、
なぜ移項ができるのか??
ということを理解していること。これにつきる。
方程式をすばやく解くことも大切だけど、仕組みをわかっていることも同時に大切だよ。覚えておこう!!
方程式のかなめの「移項」についてスッキリしたかな?? まだわからないときは、等式の性質を復習してもう一度移項を再現してみよう。
ゆっくりやればきっとわかるはず!
移項をつかって方程式をガンガン解いていこうー!
そんじゃねー。
Ken
こんちゃ!ストーブでやけどしそうになったKenだよ。
中学1年数学の山場は「方程式」。ここさえ超えてしまえばあとは楽勝なんだ。ちょっと難しそうに聞こえても辛抱強く粘ってみよう!

そんで、
前回まで「方程式を解く」ということを勉強してきたけれど、
じつは方程式を解くためにはたった1つのことを利用してやればいいんだ。
それは、
等式の性質
というやつさ。言葉を言い換えれば、
等式にはどんな特徴があるのか???
という話。これさえ理解してしまえば方程式を解くなんてちょちょいのチョイ。中学数学で勉強する「等式の性質」というものはぜんぶで4つあるんだ。
今日はめんどくさいし、せっかくだから等式の性質というものをすべて復習してみよう!
中学の数学で勉強する「等式の性質」とやらは次の4つだ。ちょっと等式というものがよくわからん、というときは等式についての記事の、
っていう2つの記事を参考にしてみてね。きっとピンとくるはずだ。うん。
それじゃあさっそく、等式の性質をみていこう!
1つ目の等式の性質は、
「左の式」と「右の式」に同じ数字を足しても等式は成り立つ!
ということ。ちょっと言葉だけじゃわかりにくいから例題をみてみよう。
たとえば超シンプルな「A = B」という計算式があったとする。
前にも習ったけど、
これは左のAと右のBの値が等しい
ということを表してるね?? そんで、この左右両方にCという数字を足してあげよう。
すると、次のようになる。
同じ数字「C」を左と右の両方に足しても、まだ成り立っているということが言えるんだ。
つまり、
A + C
と、
B + C
の値が等しいということ。これはちょっと理科でならった「てんびん」に似ているね!
てんびんの左右に同じ重さのおもりをのせても釣り合ったよね?? 等式はチョー「てんびん」に似てるんだ。等式の意味を忘れそうになったら理科のてんびんを思い出してみよう!
等式の性質を確認するためにAとかBとかCとか胡散臭い文字を使ったけど、実際の数字を使ったって大丈夫。たとえば、
2 = 2 という等式の、
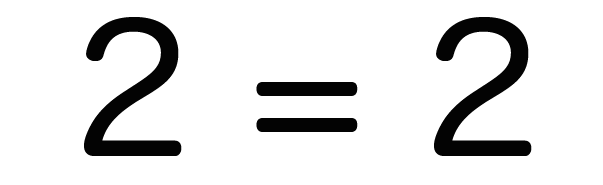
左右両方に「90」という大きな数字を足してみてもいい。
左にも右にも同じことしてやれば等式は保たれるんだ。これから紹介する残り3つの等式の性質もやってることはだいたい一緒だよ。
等式の2つ目の性質は、
「左と右の両方から同じ数字をひいても等式は成り立つよ」
というもの。1つ目の「等式の性質」の足し算を引き算に変えただけだね。
これもさっきと同じ等式の「A = B」を使って考えてみよう。
この左と右の両方から「C」という数字をひいてあげるんだ。
そうすると、
こうなるね。
同じ数字をひいても等式は成り立つってこと! 1つ目の性質とあまり変わらないね。
この等式の性質もだいたい一緒だ 。
等式の左右両方に「同じ数字」をかけても等式は成り立つってこと!
たとえばさっきの「A = B」という等式に、
Cという数字を左と右の両方にかけてあげる。
すると、こうなるね。
これが3つ目の等式の性質。1つ目と2つ目とだいたい一緒だね!。
もうそろそろ飽きてきたと思うけど、次で最後の「等式の性質」だ。
左と右の両方の式を同じ数で割っても等式は成り立つよ!
っていうのが等式の最後の性質。
さっきと同じように「A = B」という等式があったとすると、
同じ数「C」で左と右の両方の式を割ってあげればいいんだ。
こんなことをしても等式はまだ成り立つということ。こいつもこれまでの等式の性質とだいたい一緒だね。
さあ、ここまで4つの等式の性質をみてきたね。
だいたいどれも似ていたけど、つまり簡単にまとめてしまえば次のような性質になるんだ。
等式の左と右に同じ数字を足しても、ひいても、かけても、割ってもいい
ということ。
つまり、等式の左と右の計算式に同時に同じ数字を四則演算しても等式は成り立つ。
これを覚えていれば問題ないよ。
いかにも当たり前のことを言っているけれど、
これがのちのち方程式の解き方に効いてくるからしっかりと押さえておこうね。
それじゃねー!!
Ken
こんにちは、生姜湯にはまってるKenだよー
前回、「方程式とは何者か!?」ということを勉強したね。そんで、今日はその次のステップとして、
方程式の解ってなに!??
ということをみてみよう。

数学の授業でよく、
方程式を解け!
とか、
方程式を解・い・て・ね!。
とか言われるよね。じつはこの「方程式を解く」ということは、
方程式の解を求める
ということなんだ。だから、方程式の解とはなんぞや?ということがわかっていれば、あとは楽勝なのさ。今日はその方程式の「解」について解説していくね。
前回、方程式の例として、
(a+3)×9 = 45

をとりあげたね。
今日もこの方程式を例に説明していくよ。
ずばり、方程式の解とは、
正体不明の文字の正体
のことなんだ。ちょっとわかりづらいね。意味不明のマスクをかぶった文字が紛れ込んでいる等式のことを「方程式」と呼んだわけだけれども、この文字のほんとうの値・姿のことを「解」と呼ぶんだ。
たとえば、上の方程式でいえば、aの正体は2なんだ、じつは。
だって、aに2を入れてやると、
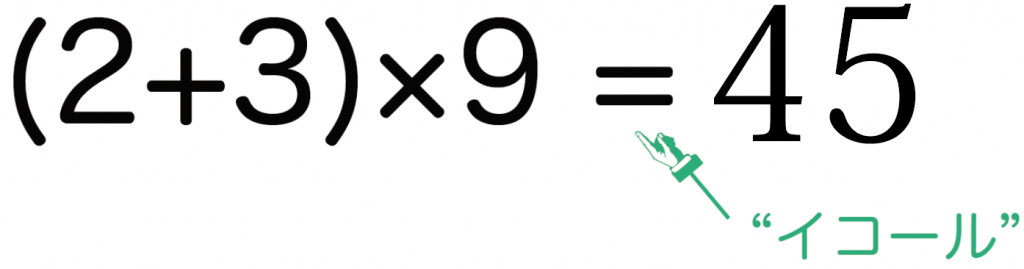
左の式が「(2+3)×9」となって計算すると「45」になるでしょ!?
これで右の値と等しくなるわけ。等式は左と右の計算式の値が等しいやつだったよね?! だからこれでいいんだ。
ちょっとかっこよく言っちゃえば、
となる。どう?? なんだかクラスで人気になりそうでしょ?。
これで方程式の解も楽勝だね。
方程式の中にまじってる正体不明の文字の真実の姿。
これが方程式の解だ。この「解」を求めるってことが「方程式を解く」ってことなんだ。
これさえわかっちゃえばあとはどんなものでも来いヤー!って感じだね!
そんじゃねー!
Ken
こんにちは、インフルエンザ倒したね。
中学1年の数学で一番やっかいなのは「方程式(ほうていしき)」という単元。
方程式なんて小学校の頃は聞いたこともなかった??
名前がかっこよすぎて仲良くなれなさそうだよね!。

今日はチョーカンタンに、
方程式とはいったい何者なのか!??
ということを振り返ってみよう。
方程式の本質を理解しちゃえばあとは問題練習をするだけでいいんだ。
ちょっと広い心をもっていれば一発で方程式と仲良くなれちゃうぜ。
試しにインターネットで検索してみよう。
この「コトバンク」というサイトによると方程式とは、
未知数を含み、その未知数が特定の値をとるときだけに成立する等式。
のことを指すらしい。
なるほど・・・・・・難しそうでよくわかんねーや。
えっ。それじゃあ困るって!?。
そうだね。
この方程式の定義をちょっとカンタンにしてやると次のようになる。
正体不明の文字が入っている等式で、文字にある値が入ると成り立つやつのこと
えっ。ちょっとカンタンになったけどまだわかりずらい!??
そうだねーじゃあこの定義をゆっくり上から順番にみてみようか。
等式ってもうすでに勉強したよね!? まだいまいちピンときていない奴は等式の記事を確認してくれ。
等式って、シンプルにいっちゃえば、
イコール(=)で結ばれている計算式のことだ。
たとえば、こんな感じ。
(2+3)×9 = 45
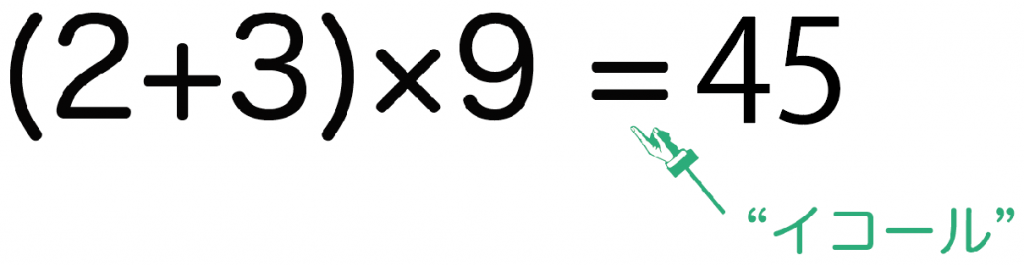
左と右の計算式が(=)で結ばれてるでしょ??
これが等式だ。等式のもっとも大きな特徴は、
右と左の計算式の値が等しいということ。
だから「等」式って呼ぶんだ。この性質を覚えておいてね。
そこでだ。
この等式という奴にわけのわからない文字が入ってくると、
等式は「方程式」と呼ばれるようになるんだ。
たとえば、さっきの等式 (2+3)×9 = 45 で、
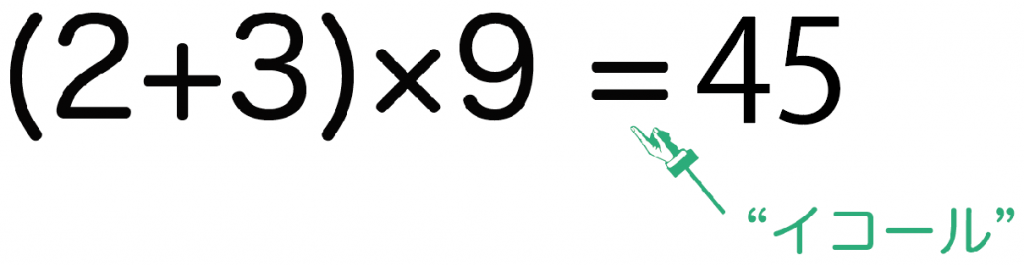
2の代わりに正体不明の文字「a」を入れてみよう。

これで方程式のできあがりだ!
もし、このaが2のとき、この等式の両辺が45になって成り立つよね。
こんな感じで、
正体不明の文字が入っていて、こいつにある特定の数字を入れると、成り立つ等式のこと
を方程式と呼んでいるんだ。
次回は、方程式の解について詳しく説明していくよ〜
それじゃねー!
Ken
こんにちは、ビタミンEが好きなKenです。
「近似値から誤差」を求める方法を勉強します。
近似値?? 誤差?? とか新しい言葉がいっぱい登場しますね!
ただ、基本を押さえてしまえば「近似値」も「誤差」も怖くないです。

今日は一緒に、近似値から誤差を計算する方法を勉強していきましょう!!
~もくじ~
近似値とはWikipediaによると、
ある数の情報を一部削って得られる値
のことです。数学っぽく言い換えると、
本当の数字をちょっと削ったもの
です。本当の数字のことを「真の値」といいますよ。
「真の値」も「近似値」もほとんど同じだということですね!! この状況を式であらわすと下のようになります。

たとえば、「有効数字の計算」の記事で取りあげた「ハンマー投げ」の例をとって説明しましょう。

http://www.irasutoya.com/2014/02/blog-post_282.htmlより
この癒し系の選手は次のような記録をたたき出しました。
測定技術が進歩しすぎて、こんなに細かい記録をとれちゃったわけです。
ただ、審判のぼくとしては大迷惑。
こんなに詳しくないくていいんです。だいたいあっている「近似値」でいいや!って思っています。
そこで、「有効数字3ケタ」という近似値を用いると、
このようにカンタンに表現できます。
有効数字は近似値の一例だというわけですね!!
「近似値」と「真の値」の差を「誤差」と呼んでいます。
誤差はつぎのような式であらわすことができます。
誤差 = 近似値 - 真の値

せっかくなので、「ハンマー投げ」の誤差を計算してみましょう。
近似値が「67.4000000」、真の値が「67.3986598」なので、

誤差は近似値から真の値をひいた「0.0013402」になります。かなり小さい誤差ですね!!
これは有効数字3ケタという近似値の正確さをあらわしています。や、やるなあ・・・・
これで近似値から誤差を計算できますね!!
有効数字でもなんでもバッチコイです。!!
それじゃねー。
Ken
<<関連記事>>
こんにちは、折り紙にはまっているKenです。
中1数学における難関の1つに、
有効数字の計算
というものがあります。
有効数字なんて見た目はかなり難しそうですよね?? 一石二鳥のような四字熟語のように見えます。

ただ、有効数字の計算なんて、
考え方さえマスターすれば楽勝!!
になるのです。いきを吹きかけるだけで有効数字を計算できるようになります。
今日は、
有効数字の考え方から計算方法まで幅広く解説します。よかったら参考にしてください。
~もくじ~
有効数字の考え方からまずはみていきましょう。
有効数字とは、
あるデータの中で意味のある数字のこと
です。そして、その有効数字の個数のことを「有効数字のケタ数」と呼んでいます。そして、有効数字で表すときは、
(有効数字)×(10のべき乗)
となります。ただし、有効数字の整数部分は必ず1ケタとしてくださいね。たとえば、67.3ではなく(整数部2ケタ)、6.73にしてください(整数部3ケタ)。
この有効数字の考え方さえわかっていれば、あとはカンタンです!!
実際の例題を確認していきましょう。

たとえば、ハンマー投げを考えましょう。ハンマー投げとはハンマーを遠くに飛ばしたものが勝つスポーツ。鍛え抜いたカラダを駆使してハンマーを遠くになげたとしましょう。
投げた距離は、超高性能メジャーにより計測しました。すると、こんな計測結果が得られたのです。
なんと、
67.3986598!!
メジャーが正確すぎて小数第7位までの細かいデータが得られました。詳細なデータほどいいデータな気がしますよね??
だがしかし、です。
こんな長ったらしい距離をいちいち記録していては日が暮れてしまいます。たぶん、記録係が逃げ出してしまうでしょう。これでは競技中止を余儀なくされます。
そこで、
有効数字をつかってデータの値をシンプルにしてあげるのです。たとえば、審判が、
有効数字3ケタで記録してーー!
と叫んだとしましょう。すると、この長ったらしい記録の左から「3ケタ」だけ抜き出します。
ここでの注意点は、
左から4ケタ目の数字を四捨五入する
ということ。つまり、有効数字にギリギリ含まれなかった数字を四捨五入してやる必要があるのです。
4ケタ目は9。5よりも大きいので、四捨五入すると3ケタ目が「3→4」になります。
よって、
この選手のハンマー投げの記録を有効数字3ケタであらわすと、
6.74×10
になります!!
以上で紹介した有効数字の考え方を踏まえて、計算方法を確認しましょう。
有効数字は次の3ステップからなります。
長ったらしいデータの数字から、
有効数字ケタ数+1
のケタ数を抜き出します。有効数字3ケタだったら4ケタというわけです。
次に、一番小さなケタ数で四捨五入します。
有効数字が3ケタだったら4ケタ目ですね!
最後に、四捨五入した有効数字と10のべき乗であらわします。
ここで注意するのは、有効数字のケタ数。整数部はかならず1ケタとしてくださいねー!
これで有効数字の計算は終了。意外とカンタンでしたね!!。
以上で有効数字の解説はおわりです。
これから有効数字をじゃんじゃんつかって理科でも数学でも活躍しちゃいましょう!!
そんじゃねー!!
Ken
<<関連記事>>
こんにちは、血糖値が高いKenです。
中学数学で「範囲(レンジ)」という言葉がでてきますよね??
「テストの範囲」の「範囲」と同じ意味です。
ただ、数学でならう「範囲」の意味はちょっと違ってきます。

今日は数学の「範囲(レンジ)」を徹底解説していきます!!
~もくじ~
それでは上から順にみていきましょう!
中学数学で勉強する「範囲(レンジ)」とはずばり、
データの最大値と最小値の差
です。これ以上でも以下でもありません。言葉だけじゃわかりにくいので、例題をみてみましょう。
たとえば、期末テストの結果がこんな点数だったとします。
国語67点、数学89点、英語47点、理科97点、社会72点・・・・・
テストの点数って一種のデータです。この5つのデータの範囲(レンジ)を求めてみましょう!
いちばん大きいデータは理科の点数で97点。
逆に、いちばん小さいデータは英語の47点。
範囲(レンジ)とは「一番大きいデータ」と「一番小さいデータ」の差のことですよね??
よって、
97-47でレンジは「50」になります!!
引き算さえ間違わなければいいのです。レンジでちんするより簡単ですね!!
範囲の計算の方法はわかりましたね??
さて、それでは範囲(レンジ)って何のためにあるのでしょうか?!? 数学のレンジなんて食べられないし、チンできないし、おいしくなさそうです。
じつは、数学の「範囲」って、
データの散らばり具合
を表したものなのです。たとえば、もしたくさん勉強して次のようなテストの点数をとったとします。

国語97、数学91、英語94、理科94、社会95・・・といったハイスコア。月々のおこづかいがアップしそうな点数ですね。
このデータの範囲って、
最大値 97 – 最小値 91 = 6
ですよね!!
まとめると、
1つ目のテストのデータより、
2つ目のデータのほうが、
データの散らばり具合が少ないといえます。その理由は、範囲(レンジ)の値が小さいからです。
範囲は代表値とならぶ、データに意見を付け加えることができる道具なのです!!
以上が範囲(レンジ)の解説です。
意見をいうときの材料として範囲(レンジ)を利用してみてください。
より多くのことがデータからわかるはずです。
そんじゃねー!
Ken
<<関連記事>>
こんにちは、かまぼこにはまっているKenです。
「資料の活用」で「代表値」がでてきますよね!??
代表値に関しては「中学数学で勉強する「代表値」とは??」という記事で解説しました。
よかったら参考にしてくださいね。

今日はもう一歩踏み込んで、
代表値の求め方
を徹底解説します!!
3つの代表値「平均値」、「中央値(メジアン)」、「最頻値(モード)」の求め方を確認していきます。テスト前にチラ見してください。
代表値の1つである「平均値」。
平均値の求め方は以下の式であらわせます。

度数分布表では「階級値」をつかって平均値を計算しましょう!
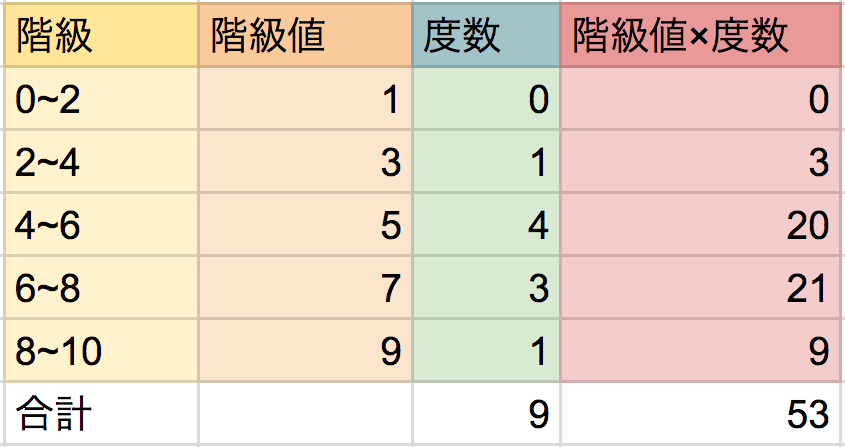
よって、「階級値×度数」を「データの合計数」でわると5.89という平均値が得られます。
平均値は3つの代表値の中で唯一、計算する値です。計算ミスをしないように気をつけましょうねー。
詳しくは平均値の求め方を読んでみてください。
「度数分布表から平均値を求めたいんだよ!」
というときはこちらの「度数分布表から平均値を求める方法」を読んでみましょう。
中央値、通称「メジアン」。
中央値とは、
データを大きい順に並べたときに真ん中になっているもの
です。中央値を求めるにはデータの並べかえが必要なのです。大きい順に!!
つぎのデータをみてみましょう。
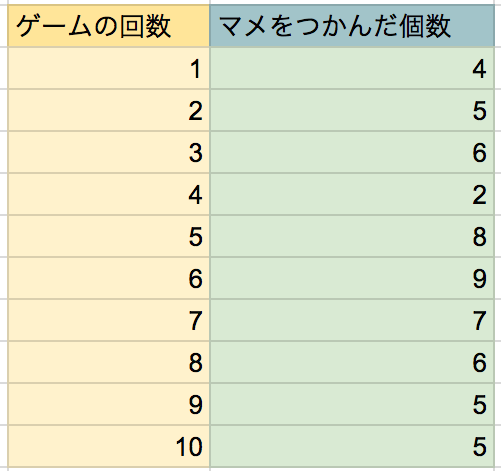
「マメをつかんだ個数」は大きい順に並んでません。むちゃくちゃな順番です。
これを大きい順に左から並べてやると、

「5」と「6」が真ん中のデータであることがわかりますね!
真ん中の数が2つある場合は、その平均が中央値となるので、この例でいうと、
(6+5)÷2
= 5.5
が中央値になりますね。この例のように、データの総数が偶数のときは真ん中の2つの数字の平均をとってあげましょう。
では、
データ数が奇数になったときは中央値はどうなるのでしょうか?
たとえば、
8, 7, 6, 6, 5, 5, 5, 4, 2
というデータが得られたとしましょう。
この場合は真ん中のデータの「5」がそのまま中央値(メジアン)になりますね。

詳しくは「中央値の求め方」を読んでみてくださいね。
最後の代表値は「最頻値(モード)」。
最頻値とは、
データの中でもっとも頻繁にでてくる数字のこと
です。最頻値では、データの全体をながめる技術が必要です。さらーっとみていちばん多いデータの値をチョイスしましょう。
ただ、ミスを防ぐためにデータを大きい順に並び替えるのも1つの手です。
この場合、「5」というデータがいちばん多く含まれているので、
最頻値は「5」!!
ということになります。
詳しくは最頻値の求め方を読んでみてくださいね。
以上で「代表値の求め方」は終了です。
をしっかりマスターして「資料の活用」であばれちゃいましょう!!
それでは!
Ken
<<関連記事>>