よくテストに出てくるのが「式の値」。
シンプルにいうと、
ある値を文字式に代入する
という問題だ。
今日は式の値の応用問題に挑戦しよう。
いきなり数字を代入したいだろうけど、ちょっと待った!
代入前にやることがあるんだ。
それは、
求めやすいように文字式を変形させること。
計算が楽になったり、問題の突破口が開けたりするよ。
例題だと、
$$2x² + xy + 2y²$$
の値を求めたいよね。
ただ、このままだと求めにくいから、文字式を変形させてあげよう。
がわかっているから、これらを使って値を出しやすいように式を変形。
具体的にいうと、
$$2x² + xy + 2y²$$
$$= 2(x+y)² – 3xy$$
のように「$x + y$」と「$xy$」だけであらわすといいね。
これなら代入しやすくなる。
あとは代入するだけ。
$$2(x+y)² – 3xy$$
に
を代入して、
$$2(x+y)² – 3xy$$
$$= 2 × 1² – 3 × (-3)$$
$$= 2 + 9$$
$$= 11$$
になるね。
こんな感じで、式の値のコツは、
代入前に式をいかに変形させるか
ってこと。
代入前に式の形を整えてみよう。
そんじゃねー
Ken
ルート関係でよく出てくるのはこの問題。

一度解きほぐせばすぐに解けるようになるよ。
知っておきたいのは、
ルートの中身が「何かの2乗」になれば自然数になること。
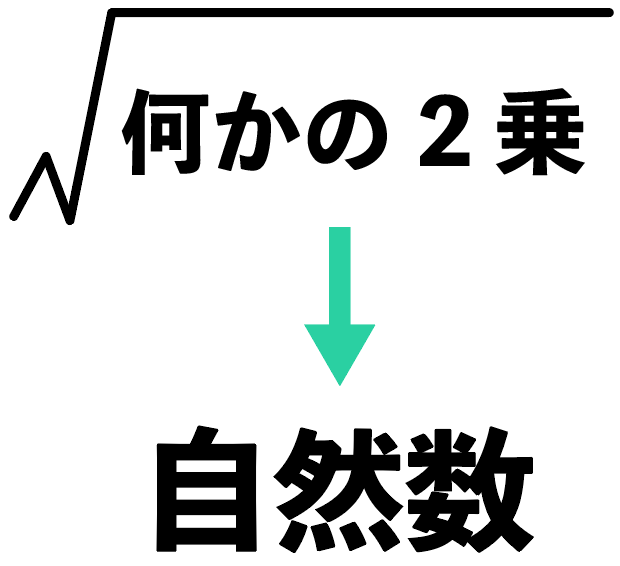
ルートの中身が何かの2乗なら、ルートが外れて自然数になるよね。
例えば、$\sqrt{5}$の2乗だったら、ルートが外れて自然数「5」になるはず。
例題ではルートの中身が「$54a$」だったから、「$54a$」が何かの数字を2乗になるように、$a$を調整すればいい。
ルートの中身を素因数分解しよう。
例題では、ルートの中身が
$54a$
だったから、$a$の前にある54を素因数分解しよう。

詳しくは「素数分解のやり方」で復習してみてね。
素因数分解すると、
$$54 = 2 × 3³$$
になるね。
素因数の指数に注目しよう。
指数とは、
数字についている乗数のこと
だ。
例えば「$3^2$」なら「2」が指数ってこと。
例題では54が
$$2 × 3³$$
に素因数分解できた。
それぞれの因数の「2」と「3」の指数をみると、
になってる。
どの因数の指数も「奇数」ってことだ。
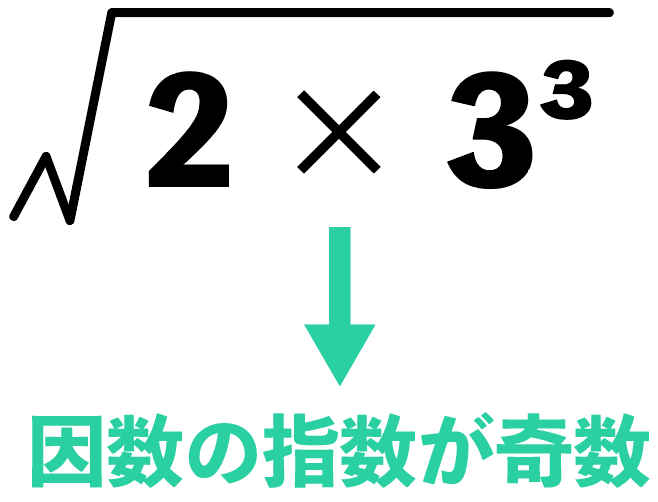
ルートが自然数になるのは、
ルートの中身が「何かの2乗」になるとき
だ。
この場合だと「2」と「3」の指数がぜんぶ偶数になるときさ。
指数が偶数になるパターンは複数考えられるけど、最小の労力で済むのが、
「2」と「3」を1つずつかける方法。
これによって、「$54 = 2 × 3³$」が
$$2² × 3⁴$$
になって、因数の指数がすべて偶数になるね。

だから、54にかける$a$は「 2と3を1個ずつかけた」6が正解だ。
$a$を6とすれば、$\sqrt{54a}$は18という自然数になるはず。

こんな感じでルートの問題と見せかけて、
素因数分解の応用問題だったわけだ。
テストに出やすいからよく復習しておこう。
そんじゃねー
Ken
二次関数の問題では、なぜか三角形が絡んでくるけど、中でも厄介なのが、
「等積変形」を使った問題だ。
例えばこんなやつ↓
右下の図で、点A、Bは関数 y=ax² と直線 l のグラフの交点で、点Aの座標は(-2, 5)、Bのx座標は1である。y = ax² の x > 0 に点Pを、△POB=△AOBとなるようにとる。点Pの座標を求めて。
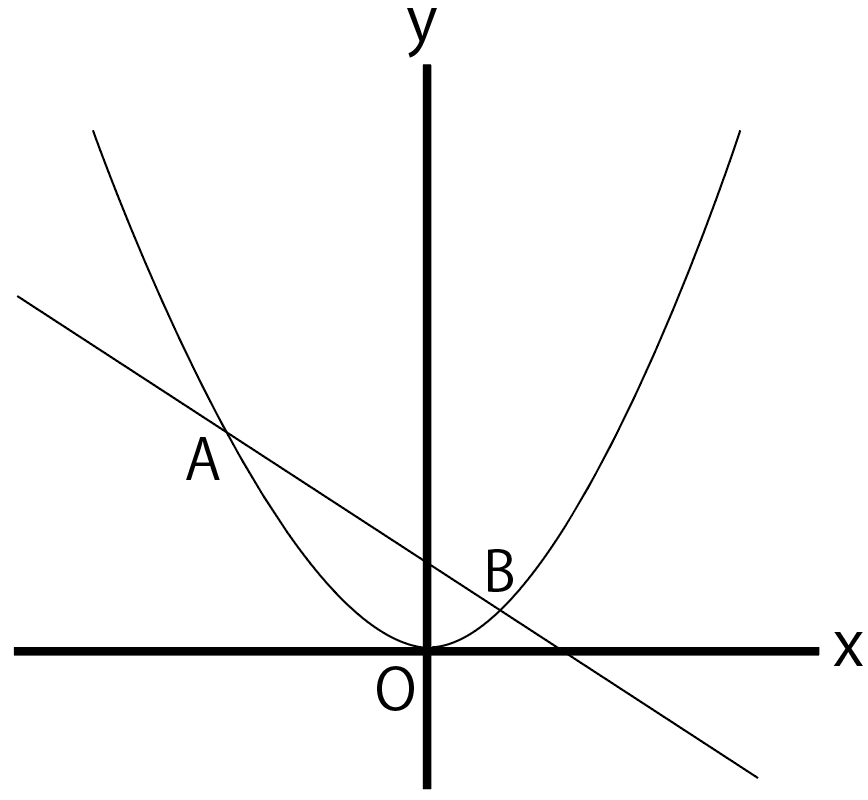
等積変形とは、
底辺が同じ2つの三角形の頂点が同じ平行線上にあると面積が等しくなる
ってやつだったね。
等積変形を忘れてたら復習してみてね。
この手の問題は5ステップで解けるよ。
最初に「大まかな流れ」を見通しておこう。
問題文では、
△POB=△AOBとなるようなPを求めなさい
といっているね。
ここで、等積変形の登場だ。
「OBに平行な直線」で、かつ、「Aを通る直線」を引いてみる。
その直線がy = ax² と交わるもう1つのAではない点が「P」になるね。

なぜなら、△POBと△AOBは辺OBを共有していて、かつ、高さが等しくなるからだ。
△POBと△AOBの底辺・高さが等しくなるから面積も等しくなるはず。

この「P」を求めればゲームクリアってわけ。
まずはBの座標を求めよう。
B は y = ax² を通っていて、かつ、x座標が1。
ってことで、y = ax² にBのx座標「1」を代入すると
y = ax²
= a
が出てくるはず。
つまり、このaがBのy座標になるから、Bの座標は、
(1, a)
になるな!
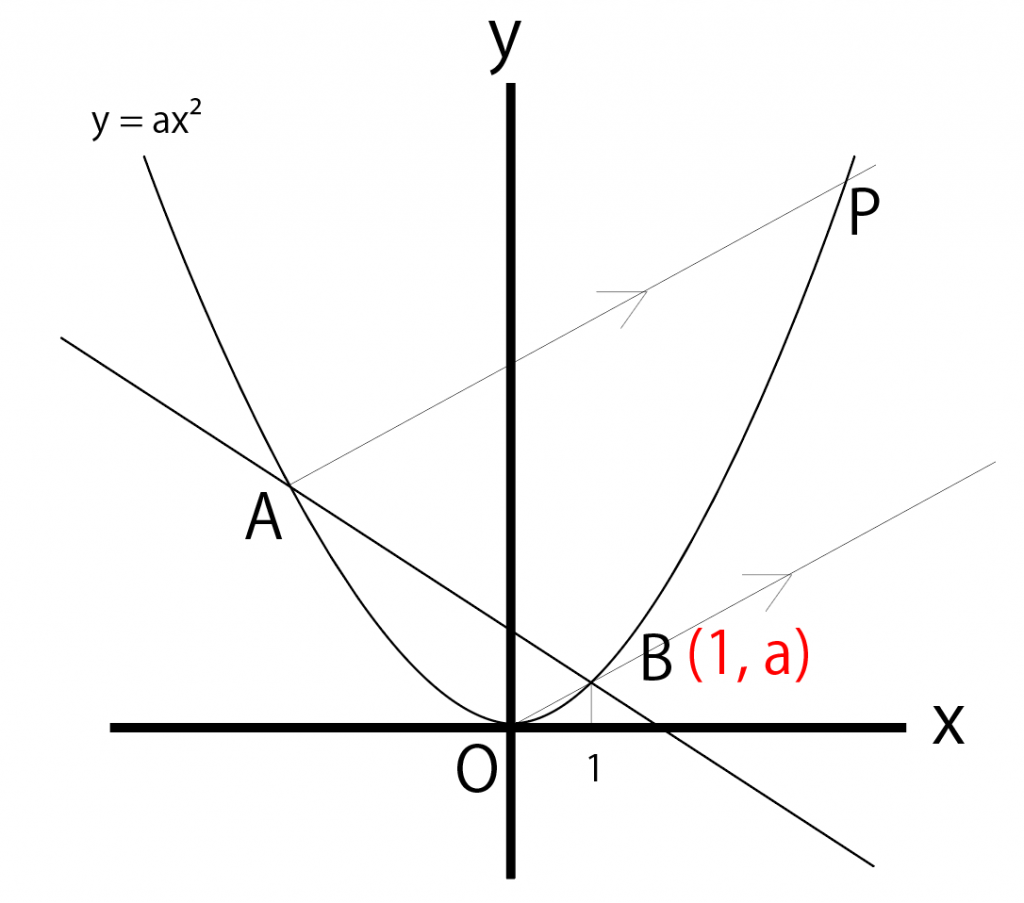
ここでOBの式を求めよう。
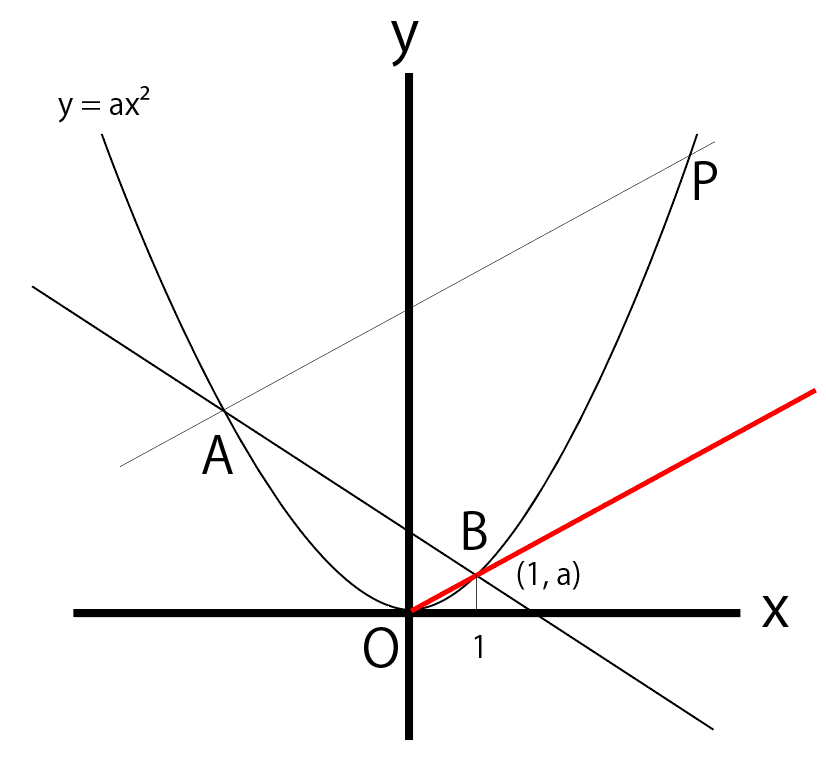
OBの式を求める狙いは、
OBの傾きをゲットすること。
APとOBは平行だから傾きが同じになるはずだからさ。
ってことで、OBの傾きはAPの式を知るための手がかりなんだ。
何もビビることはなく、OBの式を求めるのはすこぶる簡単。
原点を通っている直線だから、OBは比例の関数だね。
で、比例ということは、その傾きに当たる「比例定数」は、
(yの増加量)÷(xの増加量)
で求められる。
Bの座標は(1, a)だから、原点からのxの増加量は「1」、yの増加量は「a」。
よって、OBの傾きは、
(yの増加量)÷(xの増加量)
= a ÷ 1
= a
つまり、傾きは「a」だから
y = ax
がOBの式になるはず。
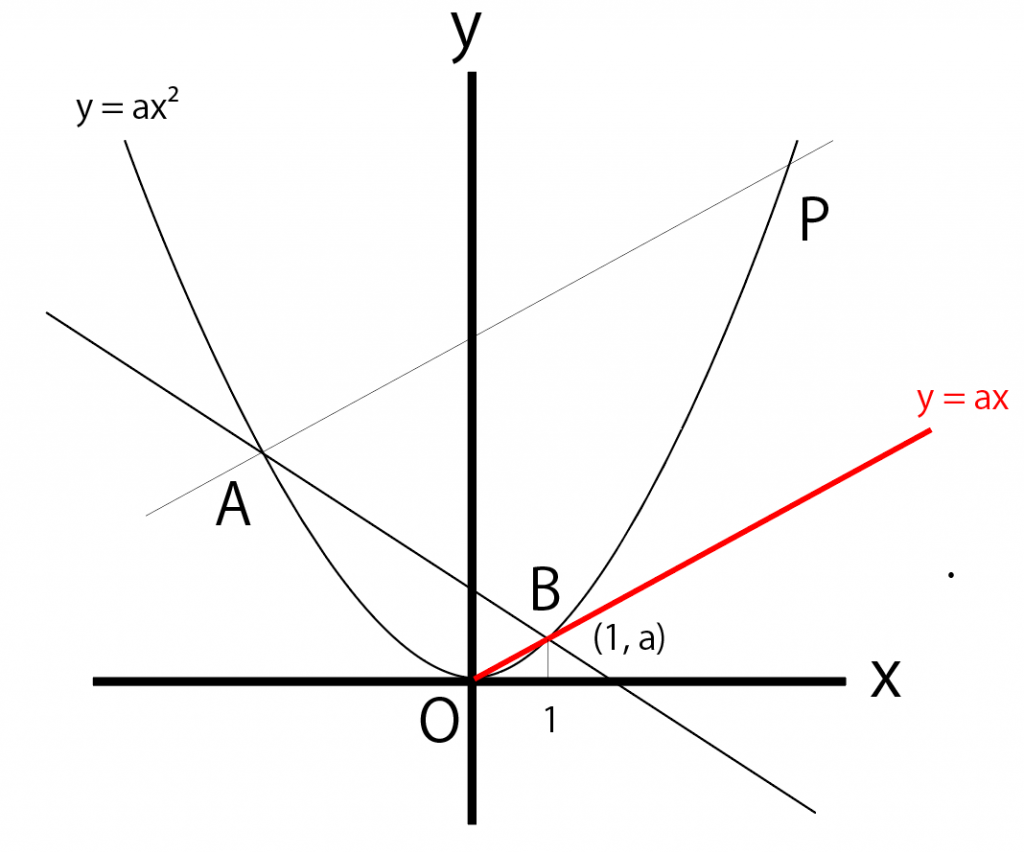
次はAPの傾きを求めるよ。
APはOBと平行な直線だから、傾きが等しい。
つまり、APとOBの傾きは両方「a」だ。
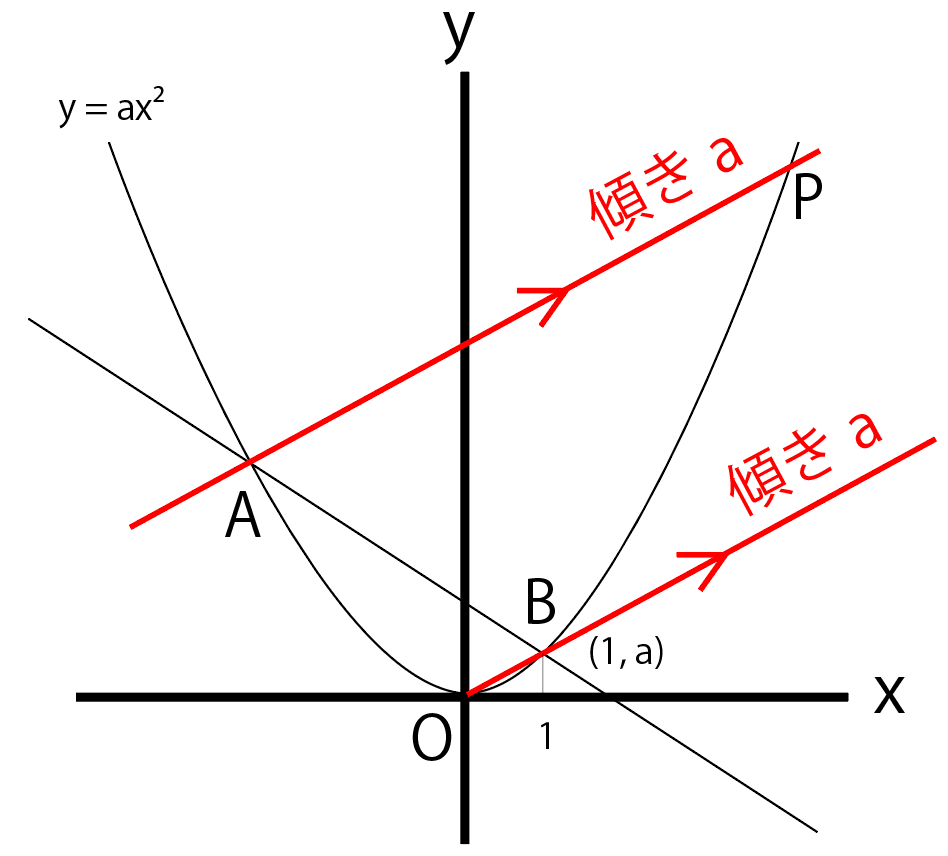
APの傾きもOBの傾きの「a」になるから、APの式の切片をbとすれば
y = ax + b
になるね。
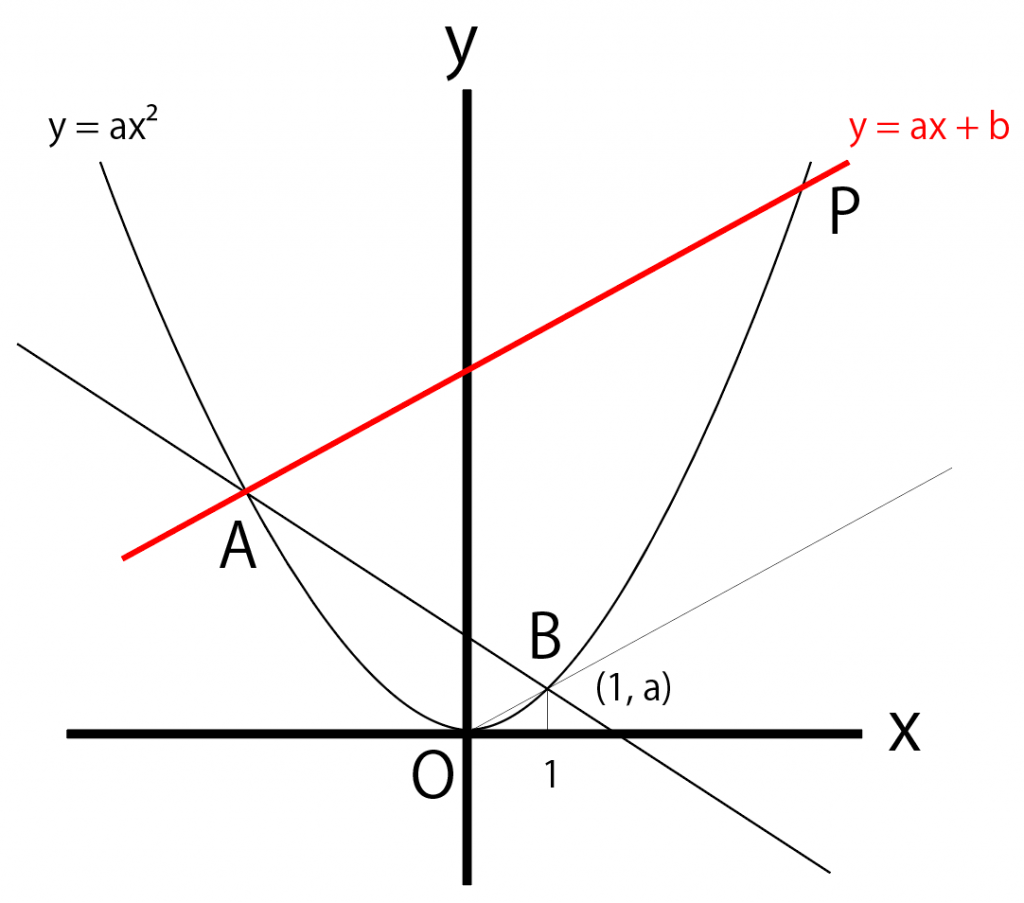
APの傾きはわかったから、あとはこいつに、
Aの座標(-2, 5)
を代入して切片bを求めてみよう。すると、
y = ax + b
5 = a × (-2) + b
b = 2a + 5
になる。
つまり、APの式は、
y = ax + 2a + 5
になる。

次は y = ax² とAPの交点を求めよう。

求めるためには、
という連立方程式を作って解けばいいね。
すると、
ax² = ax + 2a + 5
になる。
さて、ここがこの問題の一番のミソだ。
二次関数 y = ax² とAPは
の2点で交わっているね?

最初から「Aの座標」は(-2, 5)ってわかっていた。
これはなにを意味するのかというと、
を連立させてできた
ax² = ax + 2a + 5
の答えの1つはAのx座標の「x = -2」になるはず。
ってことで、すでにわかっているxの解「x = -2」を代入してaを求めよう。

ax² = a分の1 x + 2a + 5
a ・(-2)² = a分の1 × (-2) + 2a + 5
a = 4分の5
になるね。
いやあ、やっとaの正体がわかったぜ。
二次関数 y = ax² とAPの交点を求める式の
ax² = a分の1 x + 2a + 5
に戻ってみよう。
こいつにaを代入すると、
4分の5x² = 4分の5 x + 2 × 4分の5 + 5
5x² – 5x – 30 = 0
x² – x – 6 = 0
(x-3) (x+2) = 0
x = 3, -2
になる。
x=-2はAのx座標だから、もう1つの「x=3」が「Pのx座標」のはず。

あとはPのy座標を求めればいいから、y = 4分の5x² に x = 3を代入して、
y = 4分の5x²
= 4分の5× 3²
= 4分の45
になる。
したがって、Pの座標は
(3, 4分の45)
だ!!
やった!やっと終わった!
まじなげえな!
もう解きたくねえな!
こんな感じで、二次関数の等積変形を使った問題はちょっと難しい。
正直、息切れは避けられない。
この問題で大事なのは、
解き始める前に等積変形をどのように使うのか?
という見通しを立てることだ。
そして、そのシナリオに合うようにいろいろ条件を整えていけばいいんだ。
難易度が高い問題だけど挑戦してみてね。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。引き、寄せたね。
図形の問題で、なぜか狙われやすいのが
「高さがわからない台形」の面積を求める問題
だね。
例えば次のようなやつ↓
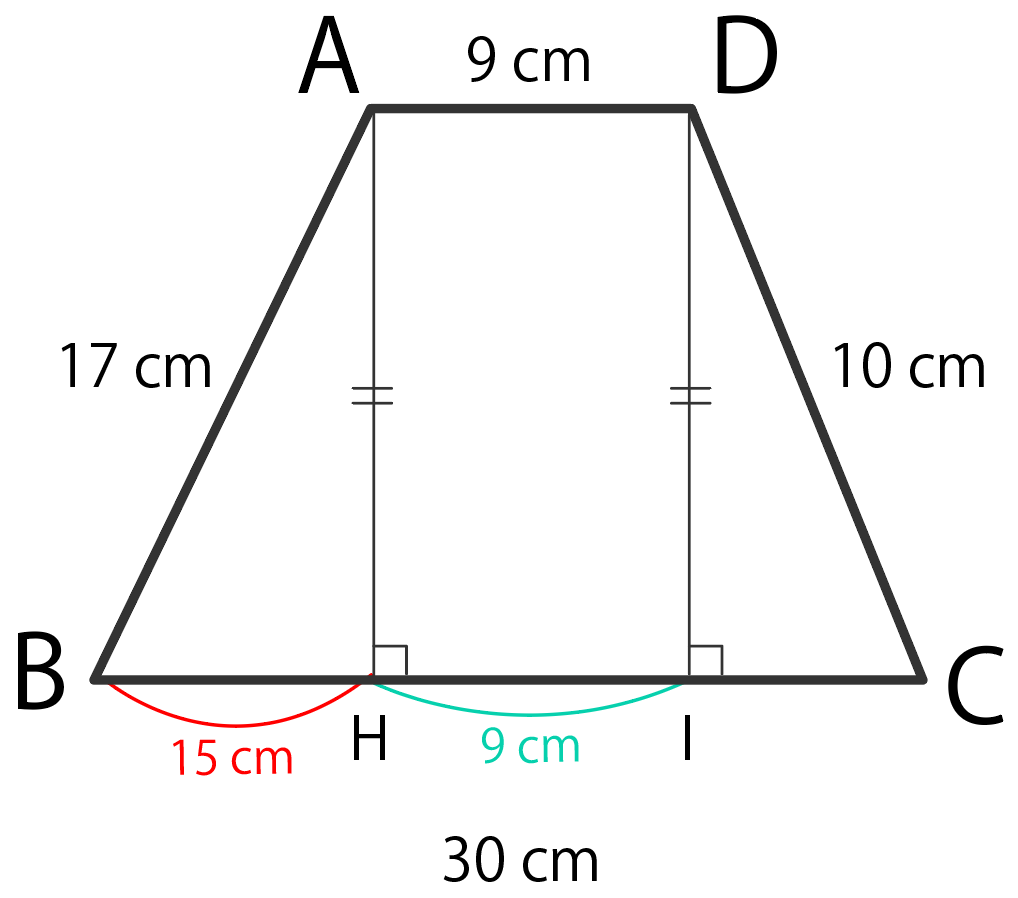
次の台形の面積を求めよ。

たしか台形の面積の求め方は、
(上の辺+下の辺)×高さ÷2
だったはず。

「上の辺」と「下の辺」の長さはわかってるけど「高さ」がわからないから、台形の面積の公式が使えねえ!
いったいぜんたい、どうすりゃいいんだろうね??
そういう時は次の5ステップを踏んでみよう。
上の辺から底辺に「垂線」をおろしちゃおう。
上の頂点から下に垂線を引けばいいよ。
ってことで、垂線は2本。
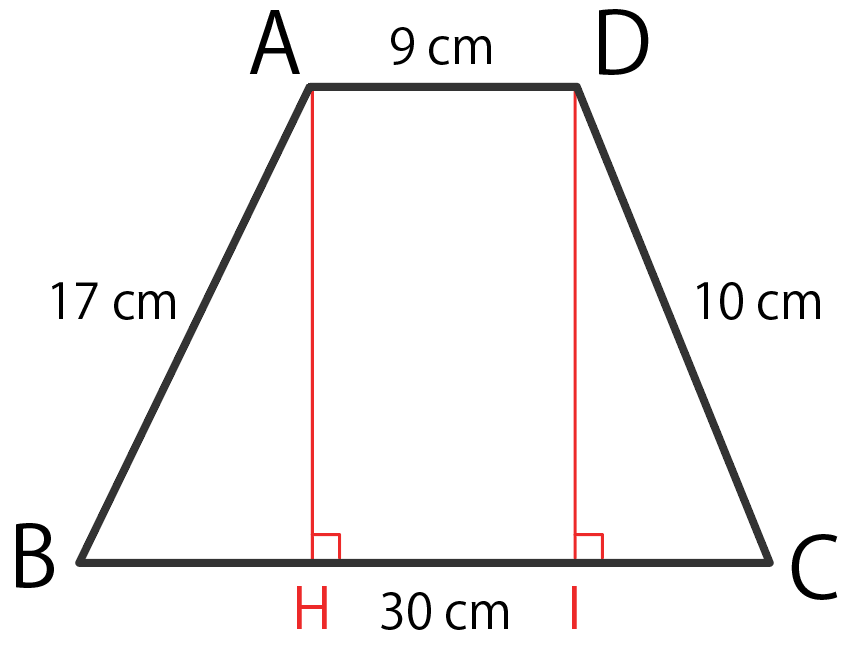
交点をそれぞれ、
としてみようか。
さっきまで「台形1つ」だった図形が、
の3つに分かれるはず。
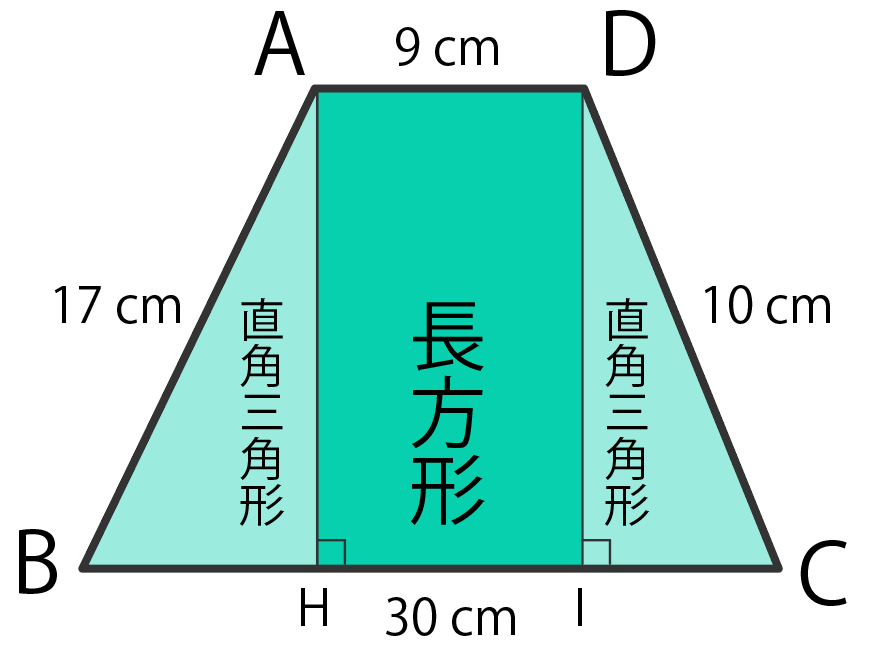
なぜ四角形AHIDが長方形なのかというと、
4つの辺が互いにそれぞれ平行
という平行四辺形の条件を満たしていて、かつ、
すべての内角が等しい(それぞれ90度)
からだね。
長方形の性質には「向かいあう辺の長さは等しい」ってやつもあった。
つまり、長方形AHIDの「HI」は向かい合った「AD」に等しいことになる。
ってことで、
HI = AD = 9 cm
だ。
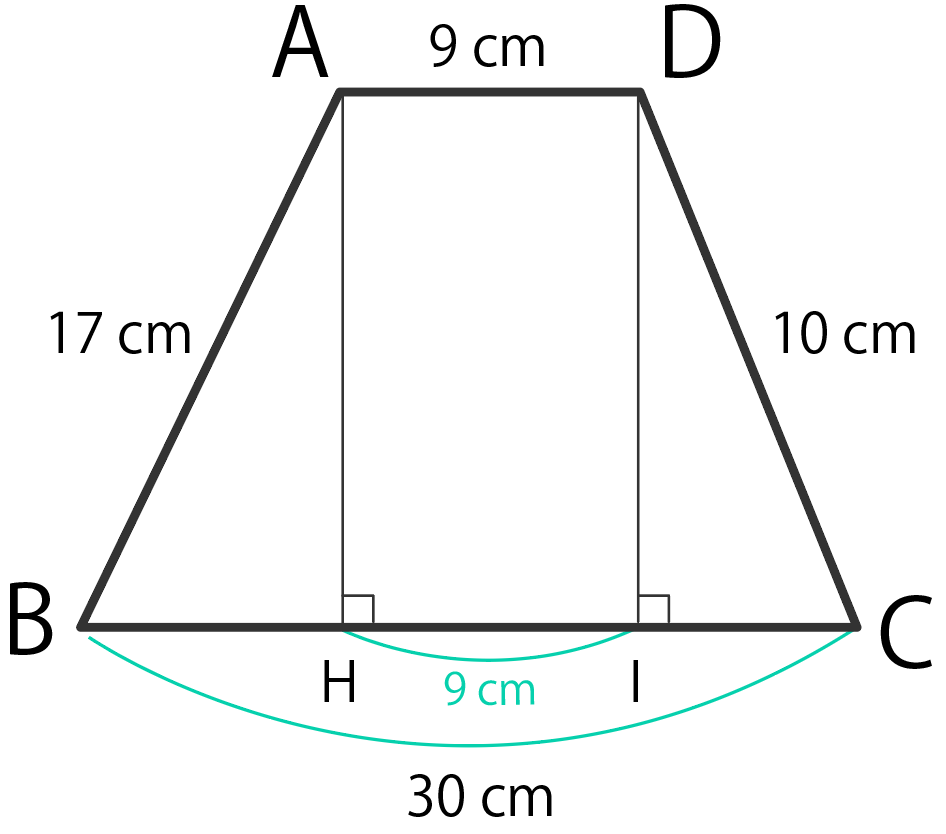
「左下の線分の長さ」をxと置いてみよう。
この例題でいうと、
BH = x cm
だね。
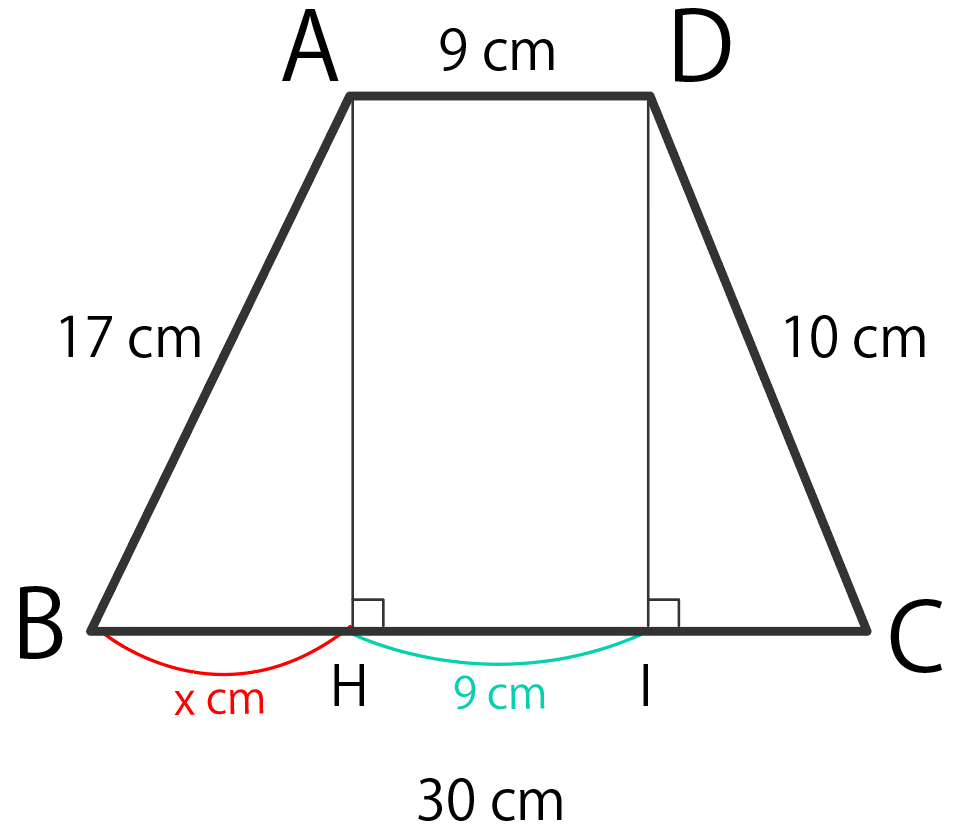
すると、ICもxで表せるね。
ICの長さは、
BC – HI – BH
= 30 – 9 -x
= 21 – x

ここで、
両サイドにできた「直角三角形の高さ」に注目。
四角形AHIDは長方形だから、向かい合う辺の長さは等しい。よって、
AH = DI
なはず。

つまり、
2つの直角三角形(ABHとDCI)の高さは等しいんだ。
この事実を利用して、二次方程式を作ってみよう。
2つの直角三角形の高さをxで表して、イコールで結べばいいんだ。
三平方の定理を2つの直角三角形で使うと、
AH = DI
AB² – BH² = DC² – IC²
17² – x² = 10² – (21-x)²
x = 15
と、「BHの長さ」が出てくるね。
あとは三平方の定理で「台形の高さ」を求めるだけ。
直角三角形ABHに注目してみると、
とわかっているから、残りのAHは、
AH² = AB² – BH²
AH² = 17² – 15²
AH = 8
になるね。

つまり、この台形の高さは「8 cm」ってわけ。
やっと台形の高さがわかったから、あとは公式を使うだけ。
台形の面積の公式は、
(上辺+下辺)× 高さ ÷ 2
だったよね?
まんま公式を使うと、
(上辺+下辺)× 高さ ÷ 2
= (9 + 30)× 8 ÷ 2
= 156
したがって、この台形の面積は「156 cm² 」なわけだ。
という感じで、「高さがわからない台形の面積」も三平方の定理を屈指すれば解けるね。
二次方程式の解き方がむずいから、二次方程式の解き方もいっしょに復習しておこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。音声入力、最高。
中3数学で勉強する方程式は「二次方程式」。
こいつは「次数が2の方程式のこと」なんだけど、解き方が6つもあるせいで、なかなかに解くのが難しい問題だね。
しかも、ただでさえ二次方程式は厄介なのに、たまに、
分数を含む二次方程式
というモンスターが出現することがあるんだ。
今日はこのパターンの二次方程式の解き方をマスターしていこう。
たとえば次のような問題があるよ。
次の二次方程式を解きなさい
X²ー3分の1X = 8
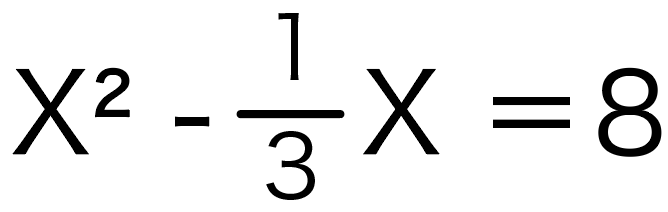
分数が紛れ込んでいる二次方程式の問題は、厄介だからこそテストや宿題に出やすい。。
次の3つのステップで瞬殺してみようぜ。
まず最初にやるべきことは、分数を消し去ること。
分数なければいつも通りの二次方程式になるから簡単になるよね。
じゃあどうやって二次方程式から分数を削除するのかっていうと、
分母の最小公倍数を両辺にかければいいんだ。
この分数の消し方は、
とまるまる一緒だね。
さて、例題の二次方程式を見てみよう。
次の二次方程式を解きなさい
X²ー3分の1X = 8
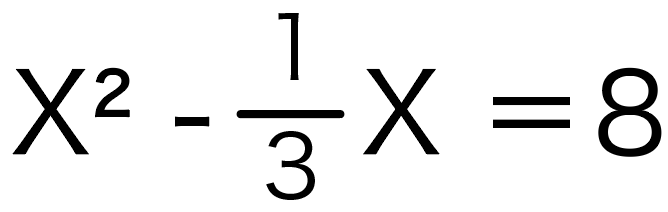
よーく見てみると分数の項が1つで、
ー3分の1X
しかない。

1つしか分数の項がないから、分母の最小公倍数はこの分母の3になるね。
ってことで両辺に3をかけてやると、
になる。

分数が消えたか確認してみてね。
あとはいつも通り二次方程式を解くだけでいいんだ。
例題を見てみよう。
3X²ーX = 24
はx2乗の項とxの項、整数の項がそれぞれ1つずつある二次方程式。
みやすいようにすべての項を左辺に寄せてみよう。
すると、こうなる↓
3X²ーX – 24 = 0
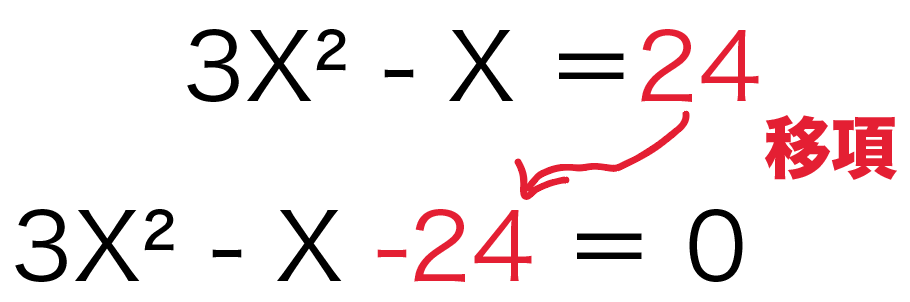
あとは二次方程式をいつも通りとくだけ。
「3X²ーX – 24 = 0」は公式で因数分解できないけど、たすき掛けの因数分解なら使えそう。
3X²ーX – 24 = 0
でたすき掛け因数分解を使ってやると、
3X²ーX – 24 = 0
(X-3) (3X+8) = 0
になるね。

たすき掛け因数分解を忘れちゃった時はこの記事で復習してみてね↓↓
(X-3 ) と(3X-8)のどっちかが0のとき、(X-3) (3X-8)が0になるから、
の2通りの等式ができるはずだね。

よって、この2つの方程式を解くと答えは、
x =3, -3分の8
だ。
以上が分数を含む二次方程式の解き方だったよ。
ポイントはやはり、
一番最初に分数を消し去るということ。
分数がなくなればいつも通りに二次方程式の解き方でとけばいいから、
の6つの二次方程式の解き方が使えるようになるんだ。
テストにも出やすいからよーく復習してこう。
そんじゃねー
Ken
やあ、Dr.リードだよ。今日は「逆」だよ。逆。
これまで勉強してきた、三平方の定理には、
三平方の定理(ピタゴラスの定理)の逆
っていうのがあるんだ。

逆は中2数学で習ったやつだったね。
忘れてるやつも多いと思うから、逆を復習しつつ、
三平方の定理でも逆が言えるのか??
を見ていこう。
=もくじ=
まずは数学の「逆」を復習してみよう。
数学の「逆」とはずばり、
ある命題の「仮定」と「結論」を入れ替えたもの
なんだ。
数学の命題とは、「正しいか、正しくないかを考える事柄のこと」だったね。
たとえば、次のような命題があるとするよ。
x =2, y = 3 ならば x+y = 5

仮定と結論をいれかえて、逆を作ってみると、
x+y = 5 ならば x =2, y = 3
になるね。

この命題の逆は正しいかな?
「x+y=5」を満たすxとyの組み合わせって「x=2, y = 3」以外にもありそうだよね?
たとえば、「x = 0、 y = 5」とかね。
だから、この場合は逆にすると命題が成り立たないね。
この例みたいに、
ある命題は正しいけど、逆は正しい場合もあるし、正しくない場合も両方あり得るんだ。
では、三平方の定理の逆はどうだろ。
三平方の定理(ピタゴラスの定理)とはこうだったな。
【三平方の定理(ピタゴラスの定理)】
直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、
a²+b² = c²
が成り立つ。

この三平方の定理(ピタゴラスの定理)で逆をつくってみようか。
三平方の定理の仮定と結論は、
だ。
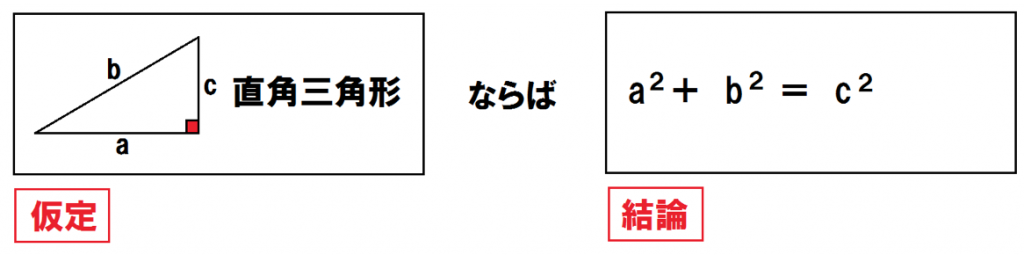
この逆をつくってみると、
になるね。
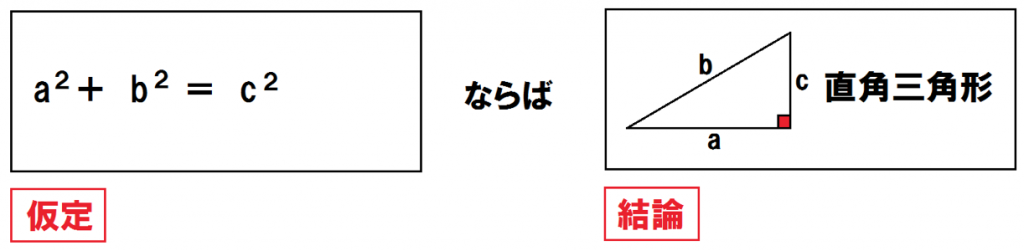
つまり、三平方の定理(ピタゴラスの定理)の逆は、
「a²+b² = c²」ならば「直角三角形である」
だ。
はてさて、これは正しいのかな?
三平方の定理の逆の証明してみるか。

わかりきってても、きっちりいくぜぃ。
下の図のような△ABCと△DEFがある。
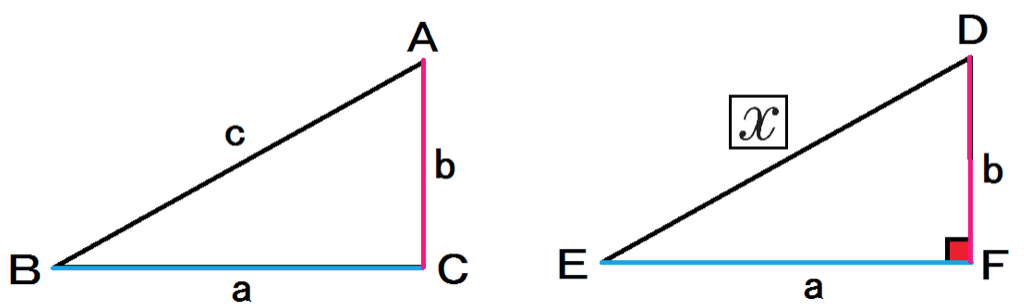
【仮定】
△ABCにおいて a²+b² = c²
△DEFは直角三角形である。
【証明】
△ABC と△DEF について、
仮定より、 a²+b² = c²・・・(1)
△DEFは直角三角形なので 三平方の定理より
a²+b² = x² ・・・(2)
(1)・(2)より、
c² = x²
c も x も正の数なので 、
c = x
△ABCと △DEF の3つの辺がそれぞれ等しいので、
△ABC ≡△DEF
よって ∠BCA =∠EFD=90°
したがって、
△ABC は直角三角形である。
この証明からわかるのは、
三平方の定理の逆も正しい!
ってこと。
中学生ならこの証明で十分かな!

三平方の定理の逆をつかった問題を解いてみよう。
練習問題
次の1辺の三角形があります。直角三角形となるのはどれですか。
(1) 3 cm 4 cm 5 cm
(2) 2 cm √7 cm √10 cm
(3) 15 cm 13 cm 7 cm
(4) 2 cm 2 cm √6 cm
(5) 2√5 cm 2√6 cm 2√7 cm
(6) 2√5 cm 2√5 cm 2√10 cm
2ステップで解けちゃうぜ。
一番長い斜辺は5 cmだから、斜辺の2乗は5² = 25。
他の2辺のに乗の和は、
3² + 4² = 25
になるね。
三平方の定理が成り立つから、直角三角形である!

斜辺は√10cmだから、斜辺の2乗は、
(√10)² = 10
になる。
他の2辺の2乗の和は、
2² + (√7)² = 11
三平方の定理が成り立たないから、直角三角形ではない。

一番長い辺の斜辺は15 cm。
斜辺の2乗は 15² = 225。
他の2編の2乗の和は、
7² + 13² = 218
三平方の定理が成り立たないから直角三角形ではない。

斜辺は√6 cmだから、斜辺の2乗は、
(√6)² = 6
になる。
他の2辺の2乗の和は、
2² + 2² = 8
三平方の定理が成り立たないから直角三角形ではない。

斜辺は2√7 cmだ。
斜辺の2乗は(√7)² = 7
他の2辺の2乗の和は、
(2√5)² + (2√6)² = 44
三平方の定理が成り立たないから直角三角形ではない。

斜辺は2√10 cmだから、斜辺の2乗は (2√10)² = 40になる。
他の2辺の2乗の和は、
(2√5)² + (2√5)² = 40
三平方の定理が成り立つから、直角三角形。

三平方の定理の逆はどうだったかな?
散々「ピタゴラスった!」から慣れたようだね。
つぎは立体で三平方の定理を使えるようになってみよう!
それじゃあな!
Dr.リード
やあやあ、Dr.リードだよ。
3年生の数学もいよいよ大詰め。
今日は、高校入試でよく出てくる、
正四角錐の高さを求める問題
を解説していくぞ。
正四角錐って、底面が正方形で、先っちょが尖ってる立体のことだったね。

ちょうど、エジプトのピラミッドが正四角錐だな。
正四角錐の高さを求めるためには、中3で勉強した三平方の定理も使っていくぞ。
正四角錐の高さの求め方はつぎの4ステップだ。
つぎの例題をいっしょに解いていこう。
練習問題
つぎの正四角錐の立体の高さを求めなさい。
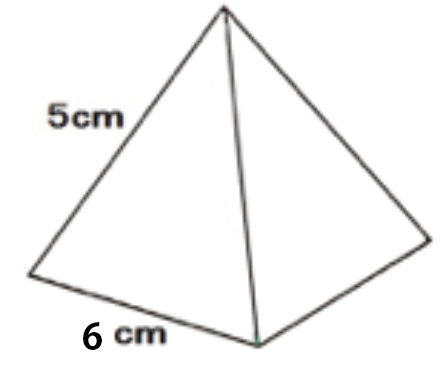
まずは、補助線をガンガン入れる。直角にも印をつけるといい。
正四角錐の中の直角三角形を見つけやすくするためだ。
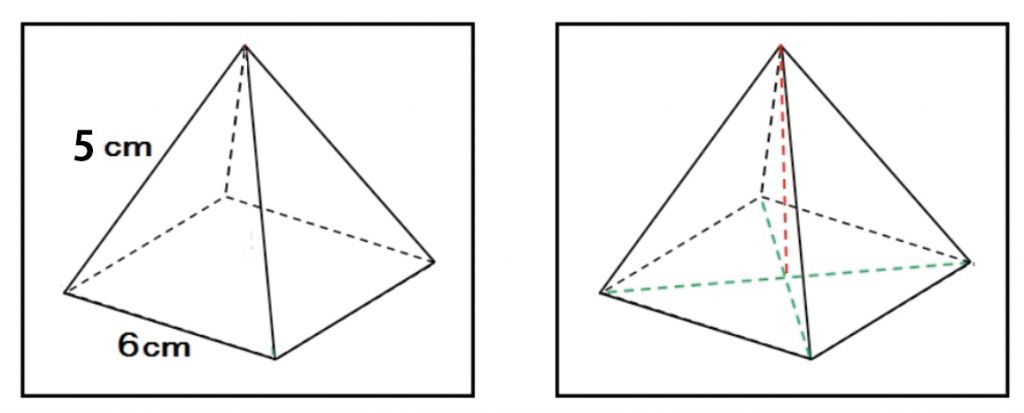
つぎは、正四角錐の底面に注目してみよう。
底面の正方形の対角線の長さを計算していくんだ。
底面は1辺が6cmの正方形だったな?
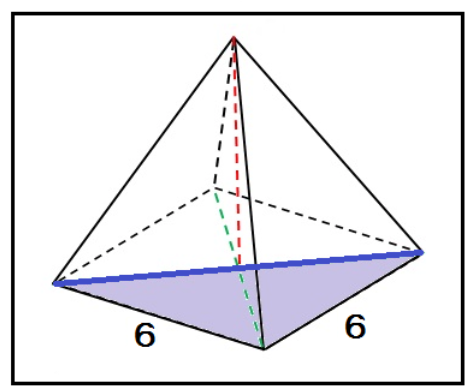
この正方形の半分の直角三角形で三平方の定理を使ってやると、
6² + 6² = x²
x = √72 = 6√2
になるぞ。
ってことは、正四角錐の底面の対角線の半分の長さは、
6√2÷2 = 3√2
だ。
つぎは、正四角錐の頂点からの垂線に注目。
垂線をふくむ直角三角形を探して、三平方の定理を使えばいいんだ。
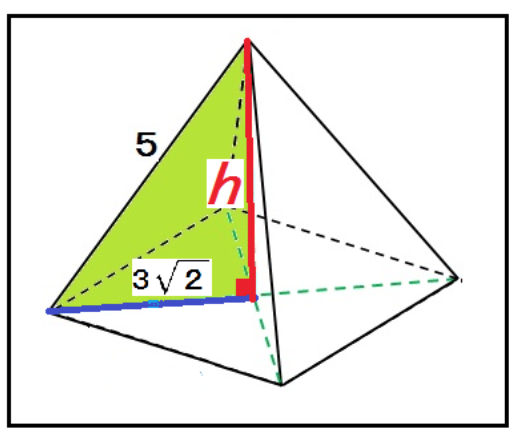
さっき見つけた正四角錐の頂点からの高さを求めてみよう。
使うのは、もちろん、
三平方の定理!
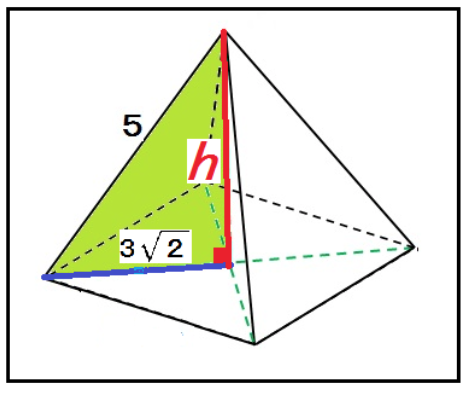
正四角錐の頂点からの高さをhとしてやると、
5² = (3√2)² + h²
h = √7
になるね。
つまり、この正四角錐の高さは√7 cmってわけ!
正四角錐の高さの求め方はどうだったかな?
つぎの4ステップで計算できちゃったな。
入試問題によく出てくるから復習しておこう。
正四角錐の高さが計算できたら次は円錐の高さに挑戦してみよう。
じゃあな
Dr.リード
tomo の中学3年生の数学の単元ごとにまとめてみたよ。
テストや試験の復習に参考にしてね!

二次方程式を解くために必要な計算方法を勉強していくよ。
二次方程式や三平方の定理で活躍する「平方根の計算方法」を勉強していくよ。
いよいよ二次方程式を解いていくよ。
二次方程式を使って次数が2の関数を勉強していこう。
相似な図形にチャレンジ!
円周角と中心角を使いこなせ!
ピタゴラスが発見した定理を駆使しよう!
統計学の基礎をマスター!
こんにちは!この記事を書いてるKenだよ。ナンは1つでいいね。
三角形の角の二等分線の定理・性質
っておぼえてるかな??
念のために復習しておくと、
「三角形の二等分線と底辺の交点」と「各頂点の長さの比」が、他の辺の2辺と等しい
っていう定理だったよね??
言葉じゃわかりづらいから図をみてみよっか。
たとえば、
の△ABCで、∠Aの二等分線との交点をDとすると、
AB : AC = BD : DC = a : b になってるんだ。
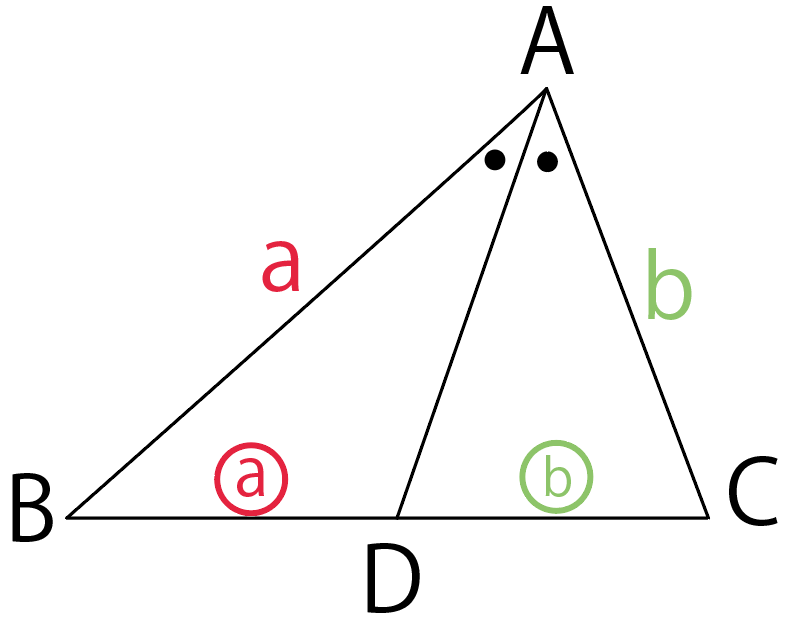
なぜ、三角形の角の二等分線の性質が使えるのかわからない??
そういうときは、角の二等分線の定理の証明の記事を読んでみてね。
今日はこの定理を使った問題を解説していくよ。
つぎの問題を解いてみよっか。
つぎの△ABCにおいて、線分BDの長さを求めなさい。
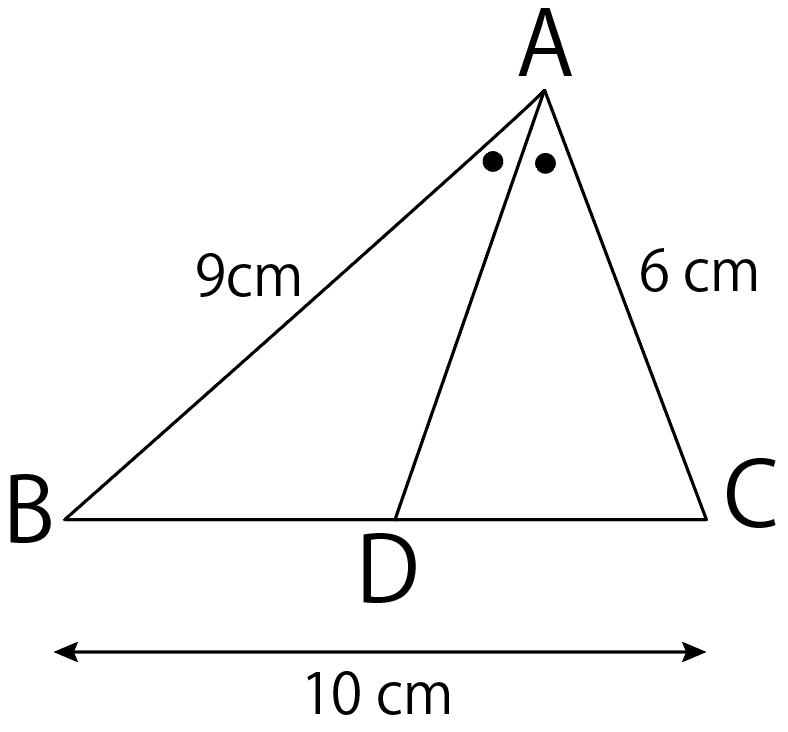
このタイプの比の問題はつぎの3ステップで解けちゃうんだ。
まずは、三角形の2つの辺の比を求めてみよう。
練習問題でいうと、
の2辺だね。
こいつの辺の比を求めてみると、
AB : AC = 9 : 6 = 3 :2
になる!
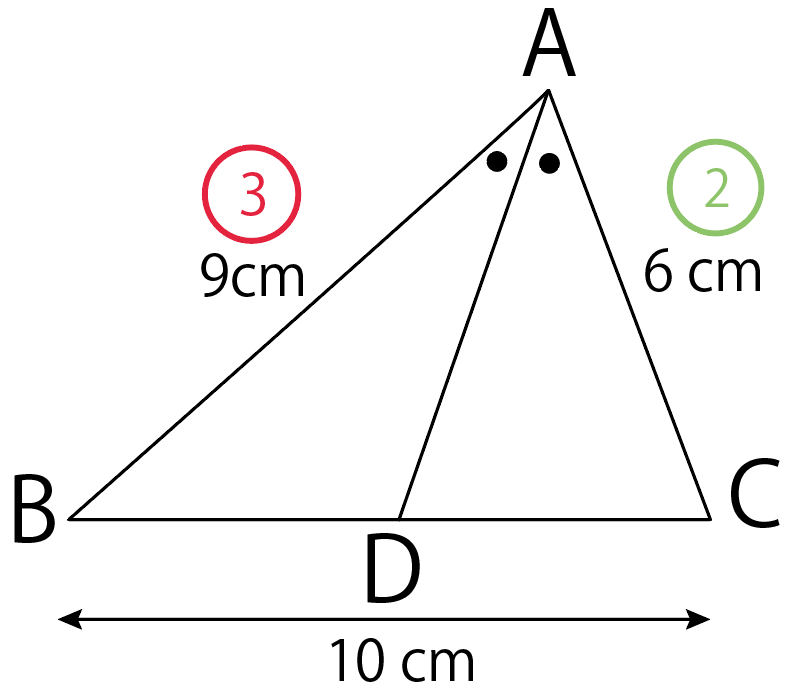
これが第一ステップ。
いよいよ三角形の角の二等分線の定理の出番だ。
さっき求めた「三角形の2辺の比」と「二等分線と底辺の交点でできた線分の比」が等しいってことがいえるからね。
練習問題でいうと、
AB : AC = BD : DC
が言えるわけ。
ステップ1で、AB : AC = 3 : 2がわかったから、
BD : DC = 3 : 2
ってことがわかるね。
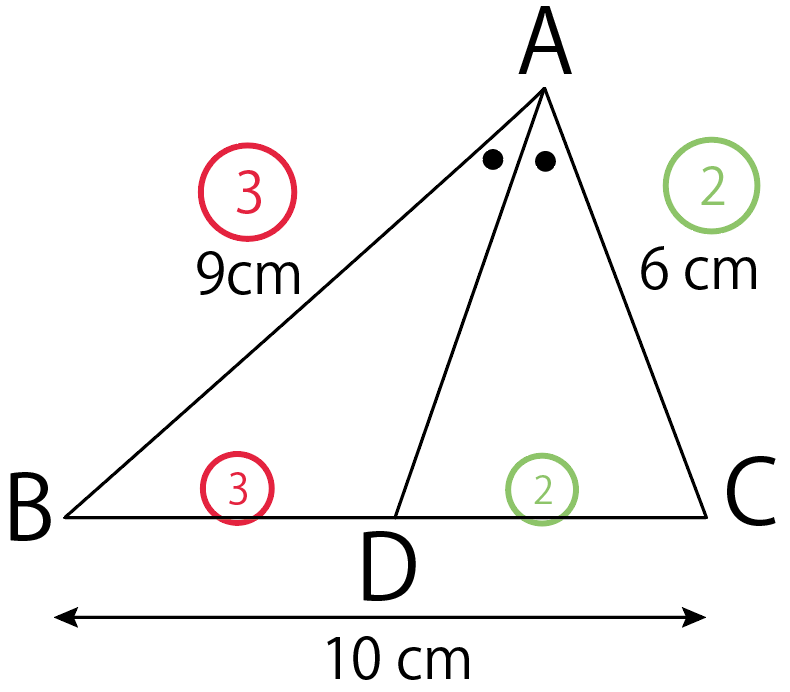
これが第二ステップ!
求めた辺の比を使って、辺の長さを計算しよう。
練習問題でいうと、
BD : DC = 3 : 2
っていう比をつかって、BDの長さを求めればいいね。
底辺BCの長さは10cmだったから、
BD = 10 × 5分の3 = 6 cm
になるんだ。
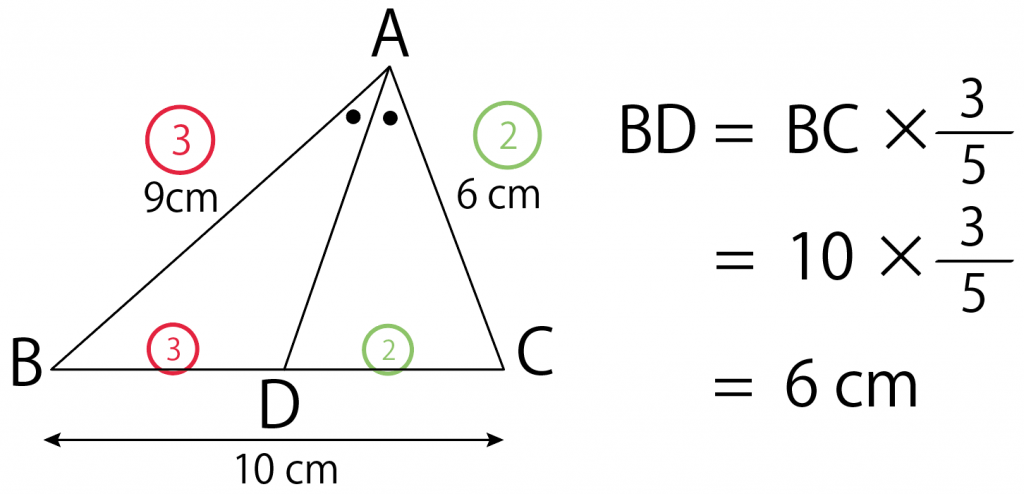
角の二等分線の性質の問題はどうだったかな??
の3ステップでだいたい解けそうだったね。
最後につぎの応用問題を解いてみよう!
つぎの△ABCにおいて、AE : EDを求めなさい。
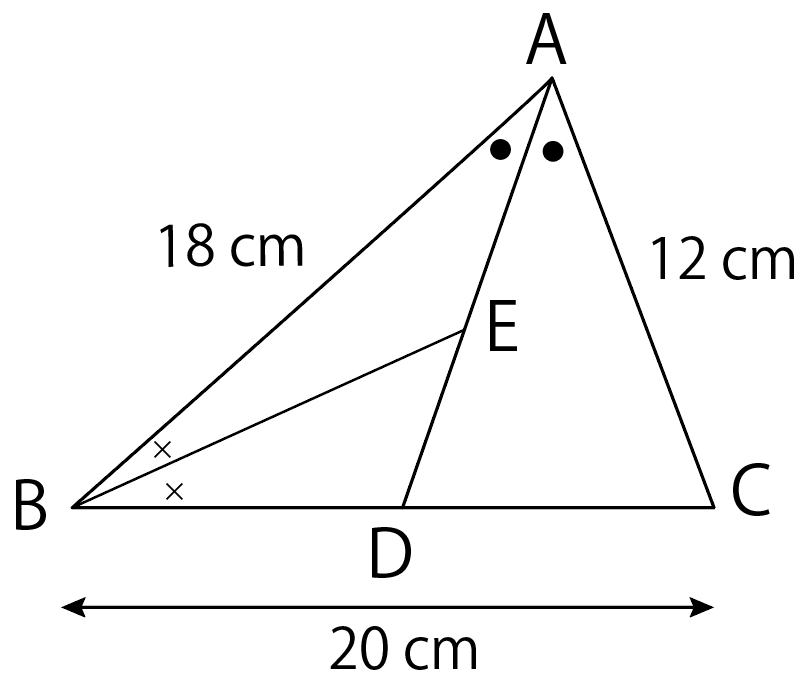
そんじゃねー
Ken
こんにちは!この記事を書いてる Kenだよ。分子を振動させたね。
中2と中3数学の平面図形で、
三角形の「合同条件」と「相似条件」
を勉強してきたよね。

両方とも数学の証明のために必要なアイテムだから、テスト前には覚えなきゃいけないね。
念のためおさらいしておくと、
だったね。
でもさ、この2つの条件ってちょっと似てない??
ごちゃ混ぜにしちゃうことあるよね。
そこで今日は、
三角形の合同条件と相似条件をごちゃ混ぜにしないために、整理して覚えてみよう!
合同条件と相似条件の似ているところと、違うところを中心に復習していくよ。
三角形の合同条件と相似条件をうまく覚えるために、3つの種類に分類してみたよ。
| 3つの何かが等しい条件 | 2つの角が等しい条件 | 2辺を角で挟んだ条件 | |
|---|---|---|---|
| 合同条件 | 3つの辺がそれぞれ等しい | 両端の角とその間の辺が等しい | 2つ辺とその間の角が等しい |
| 相似条件 | 3つの辺の比がすべて等しい | 2つの角がそれぞれ等しい | 2つの辺の比とその間の角が等しい |
まず1つ目の条件の種類は、
3つの「何か」が等しいやつだ。
合同条件と相似条件をそれぞれ見ていこっか。
「3つの辺の長さ」がすべて等しいっていう条件は合同条件だ。
この条件を満たす三角形たちは合同である、ってことが言えるわけね。
たとえば、次の2つの△ABCと△DEFを想像してみて。
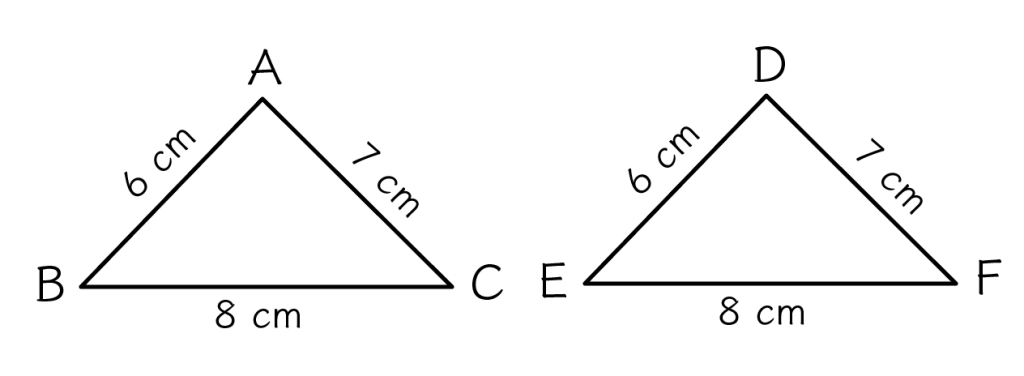
と、
この2つの三角形は合同って言えるんだ。
なぜなら、すべての3つの辺の長さがそれぞれ等しいからね。
「3つの辺の比」がすべて等しいとき、2つの三角形は相似って言えるんだ。
たとえば、2つの△ABCと△DEFを想像してみて。
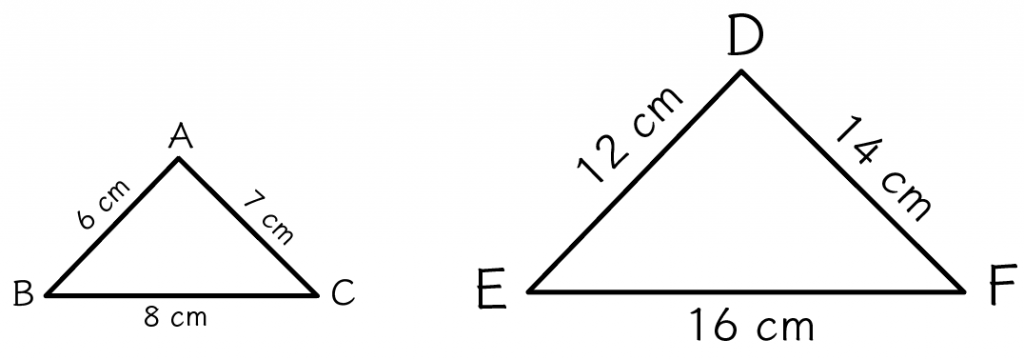
と
だ。
この2つの三角形は相似になってるはず。
なぜなら、
になっていて、すべての辺の比が全部1:2で等しくなってるね。
つぎの条件は、2つの角が等しい条件だ。
2つの角が等しいことを使った条件が、なんと偶然にも合同条件と相似条件に1つずつ存在しているんだ。
まず三角形の合同条件には、
1つの辺とその両端の角がそれぞれ等しい
っていう条件があるよ。
つまり、
1つの辺が等しくて、それを挟んでいる2つの角が等しかったら合同が言えるってわけね。
たとえば、つぎの2つの△ABCと△DEFを想像してみて。
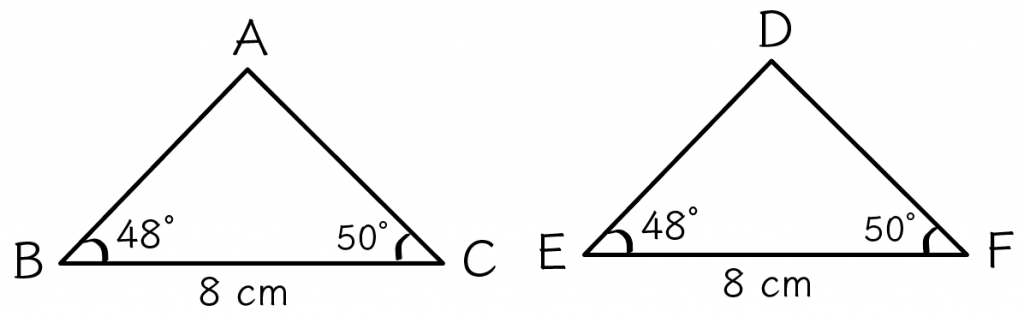
と、
この2つの三角形はへんのひとつの辺の長さが等しくて、その両端の額の大きさが等しいよね。
だから、この2つの三角形は合同であると言えるんだ。
ふたつめの相似条件は、2つの角がそれぞれ等しいっていうやつだね。
この相似条件は1番簡単で、でてきやすい相似条件なんだ。
たとえば、次の△ABCと△DEFを想像してみて。
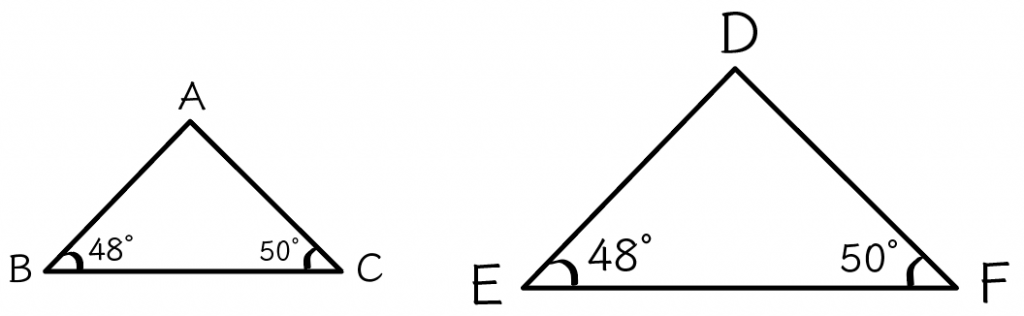
この場合、2つの三角形は、「2つの角がそれぞれ等しい」っていう相似条件に当てはまるから、相似であるといえるんだ。
つぎは、2つの辺が角を挟んじゃってる条件だ。
合同条件と相似条件には2つあるよ。
最後の合同条件は、
2つの辺との間の角がそれぞれ等しい
ってヤツ。
等しい辺たちが等しい1つの角を挟んでいれば、2つの三角形は合同って言えるんだ。
たとえば、つぎの△ABCと△DEFを想像してみて。
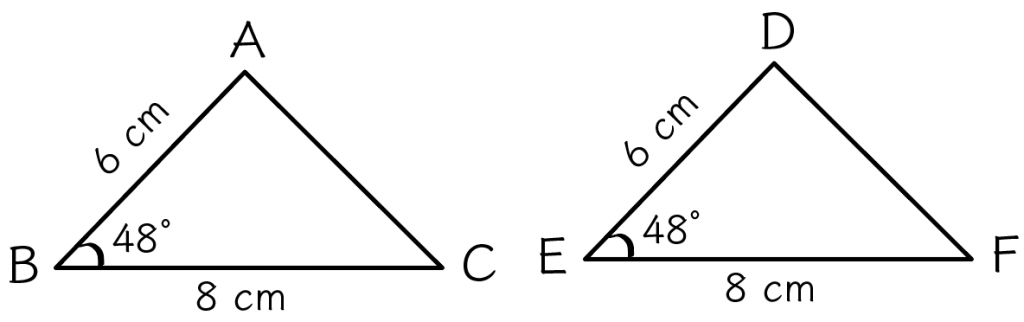
と、
この2つの三角形は、2つの辺(BCと EF、 ABとDE)が等しくて、
なおかつ、その辺に挟まれた間の角(∠ABC と∠DEF)が等しいから合同って言えるんだ。
最後の相似条件は、
2組の辺の比とその間の角がそれぞれ等しい
ってヤツね。
つぎの△ABCと△DEFを想像してみて。
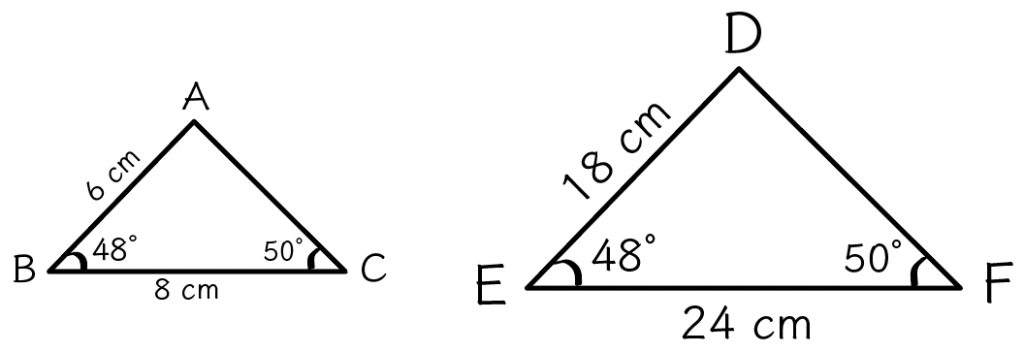
と、
この2つの三角形は相似なんだ。
なぜなら、
で2組の辺の比が1:3で等しくなっていて、なおかつ、その2辺の間に挟まってる角の、∠ABCと∠DEF が等しくなってるからね。
三角形の合同条件と相似条件は思い出せたかな??
最後にもう一回復習してみよう。
| 3つの何かが等しい条件 | 2つの角が等しい条件 | 2辺を角で挟んだ条件 | |
|---|---|---|---|
| 合同条件 | 3つの辺がそれぞれ等しい | 両端の角とその間の辺が等しい | 2つ辺とその間の角が等しい |
| 相似条件 | 3つの辺の比がすべて等しい | 2つの角がそれぞれ等しい | 2つの辺の比とその間の角が等しい |
どちらも証明問題に必要な条件だから、しっかりテスト前には覚えておこうね。
そんじゃねー
Ken
どうも、Drリードだぞい。
中3数学では、
三平方の定理(ピタゴラスの定理)を勉強してきたよな?
簡単に復習すると、
直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、
a²+ b² = c² が成り立つ
ってやつだったな。

さあ、この定理を使いこなせるようになるんだぞ。
今回はそのための基礎トレーニングだ。
三平方の定理をつかった問題でよく出てくるのは、
直角三角形の辺の長さを求める問題。
今日はこの問題を4つのパターンに分けてみたぞ。
問題集では、いろいろな直角三角形がでてくるし、簡単なのも難しいのも混じっているからな。
初めは解けなくっても、がっくりこないで、
負けんぞ!!
と構えとけ。

まず1つ目の問題は、
直角三角形の辺の長さを三平方の定理の公式で求めるタイプ。
これは、
三平方の定理の公式に、辺の長さを代入して計算するだけだから簡単だ。
たとえば、つぎの練習問題な。
練習問題1.
つぎの直角三角形の辺の長さxを求めてください。
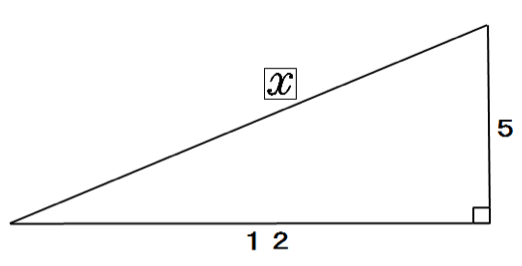
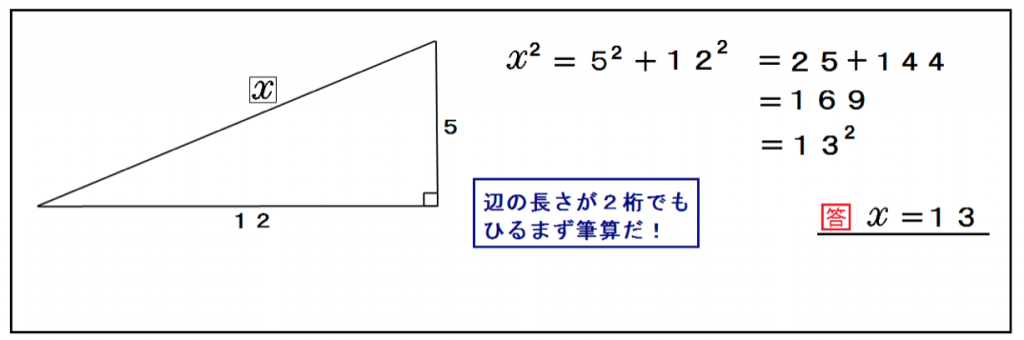
辺の長さが2桁でも気にすんな。
三平方の定理(ピタゴラスの定理)の公式にぶち込めばいいんだ。
x² = 5² + 12²
x = 13
直角三角形と言えども、いつも右下に直角が来るとは限らんぞ。
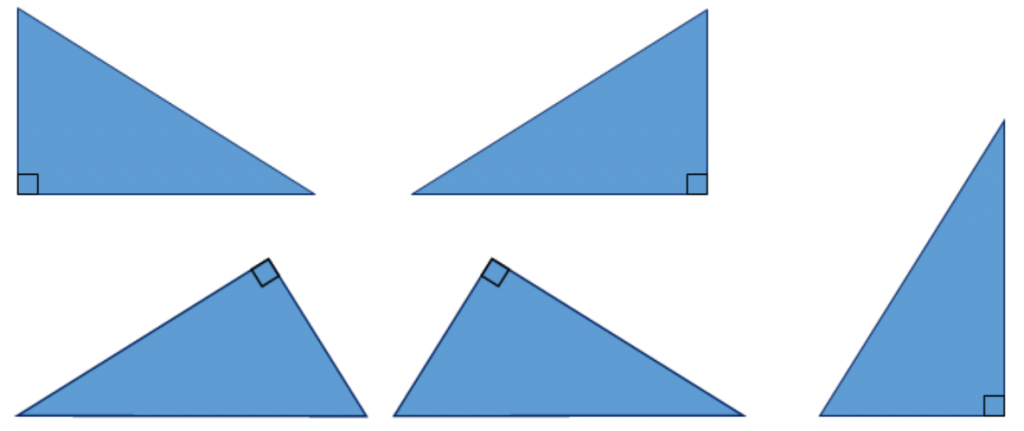
なっ。向きが変わると、斜辺がどれなのかうっかりしてしまうよ。
要注意だな。
2つ目のタイプは、
三平方の定理の計算に「平方根・ルートの計算」が混じってるやつだ。
たとえば、次のような練習問題。
練習問題2.
つぎの直角三角形の辺の長さxを求めてください。
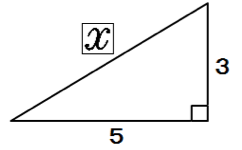
三平方の定理で直角三角形の辺の長さを計算してみると、
x² = 3² + 5²
x = √34
になるね。

答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。
つぎは、直角二等辺三角形の辺の長さを三平方の定理で計算する問題。
たとえば、三平方の定理を発見したピタゴラスも悩んだと知られる次の問題だ。
練習問題3.つぎの直角三角形の辺の長さxを求めてください。
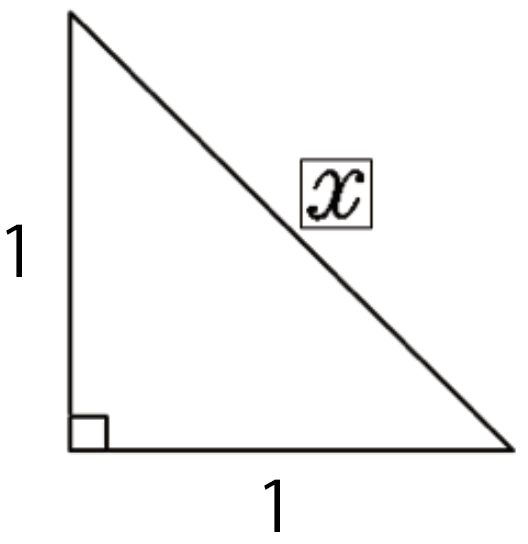
直角二等辺三角形だけど、さっきの計算問題と同じだ。
三平方の定理の公式を使ってやると、
x² = 1² + 1²
x = √2
になるぞ。
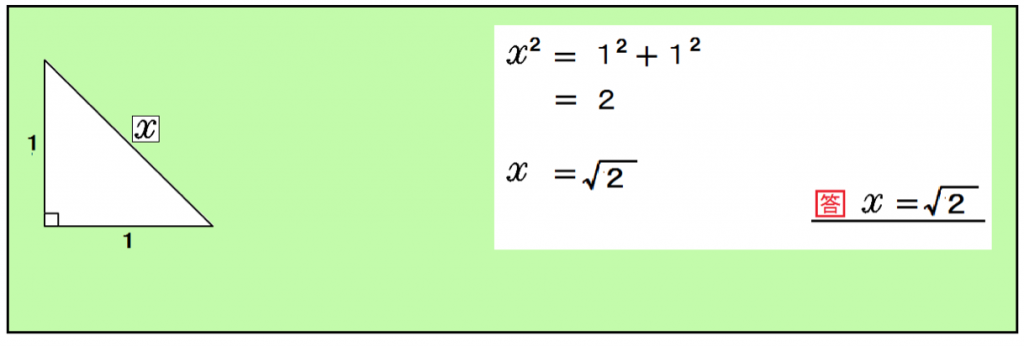
この直角二等辺三角形からピタゴラスは「無理数」を発見したと言われているんだ。
でも、ピタゴラスの生きてた時代は、まだまだ自然科学より宗教の勢力の方が主流でな。
ピタゴラス学派がうっかり、そして見事にピタゴラスの定理を見つけたんだが、
2乗して2になる数なんて、まだ見つかってなかった。
やや、これを発表したら、世の中大変なことになる・・・・
ってんで、長いこと秘密にしてたらしいぞ。

今は平和だ。
無理数はある!!と大声で言えるいい時代だ。(。)
つぎは、
直角三角形が2つくっついてる問題な。
たとえば、次の練習問題だ。
練習問題4.
つぎの直角三角形の辺の長さxを求めてください。
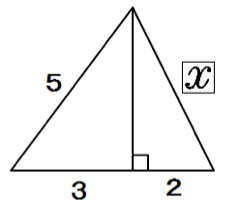
このタイプの問題では、高さを新しい文字で置いて2つの三角形の辺を出していくぞ。
まず、大きい三角形の高さをyとしてみよう。
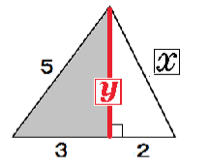
まず、灰色の直角三角形でyを計算してみる。
5² = 3² + y²
y = 4
そして、残りの白い直角三角形でxを出せばいいのさ。
x² = 4² + 2²
x = 2√5
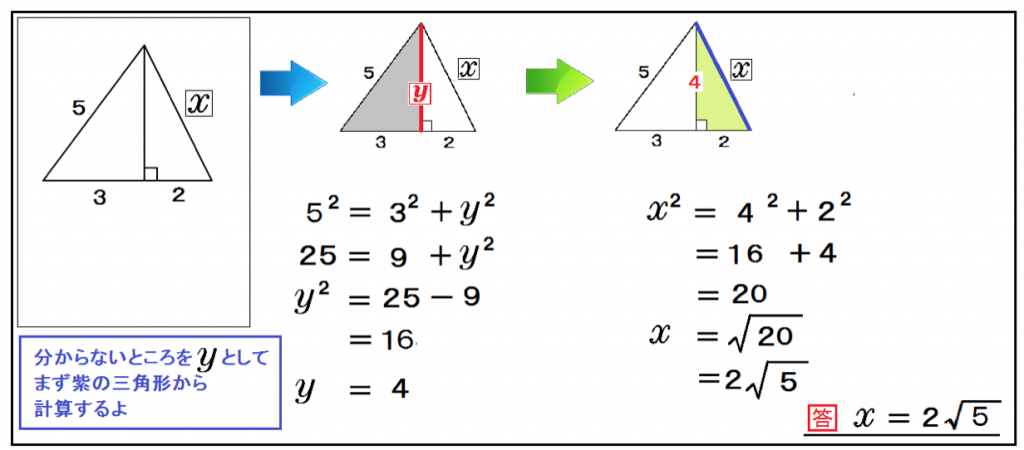
解き方大体わかっただろ??
じゃあつぎの計算問題にもチャレンジしよう。
練習問題5.
つぎの直角三角形の辺の長さxを求めてください。
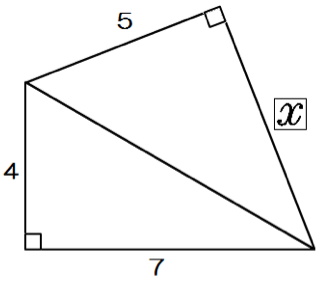
この問題も解き方はおんなじだ。
まず、真ん中の辺をyとして、yから計算すればいいんだね。
y² = 4² + 7²
y = √65
つぎはxを計算!
65 = 5² + x²
x = 2√10
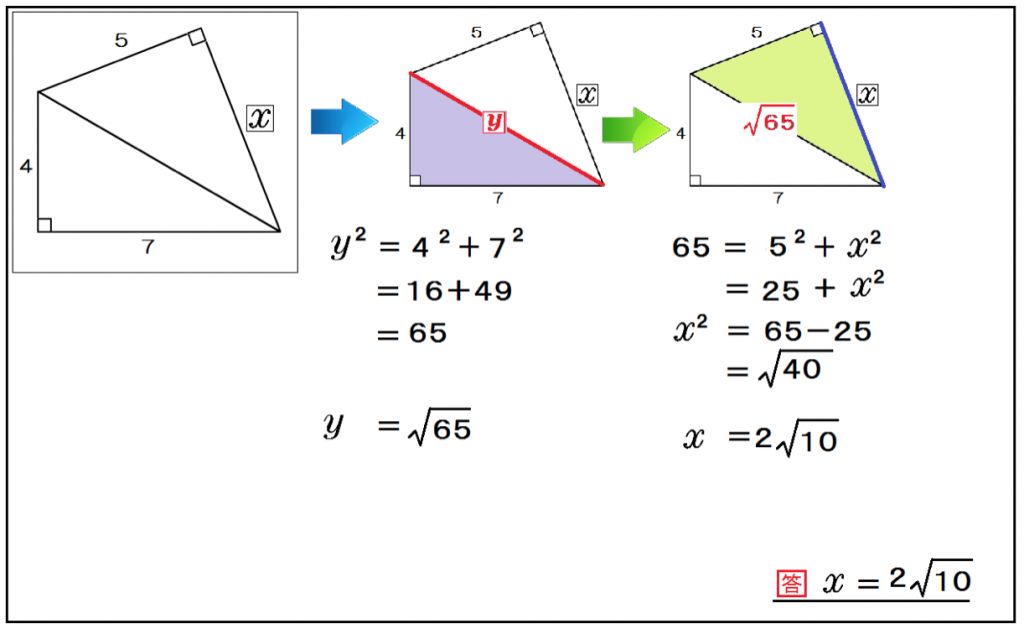
三平方の定理で、直角三角形の辺の長さを求める問題はどうだった?
今日勉強した問題のパターンは4つだったな?
これだけの基本パターンやったら、少しは自信がついたな。
慣れるまではピタゴラスの定理の式に丁寧に数値を代入してくれ。


それじゃあな
Drリード
こんにちは!この記事を書いてる Kenだよ。ゆれた、ね。
中3数学で相似を勉強していると、
中点連結定理(ちゅうてんれんけつていり)
を習うよね??
中点連結定理とはその名前の通り、
三角形の辺の中点を連結したときに使える定理のこと
をいうんだ。
三角形の2つの辺の中点を結んであげるとね、
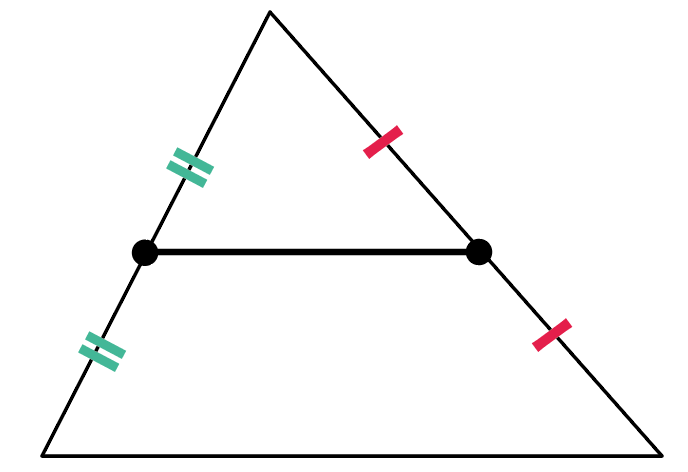
なんと、その中点を結んでできた辺の長さは、底辺の長さの半分になっていて、
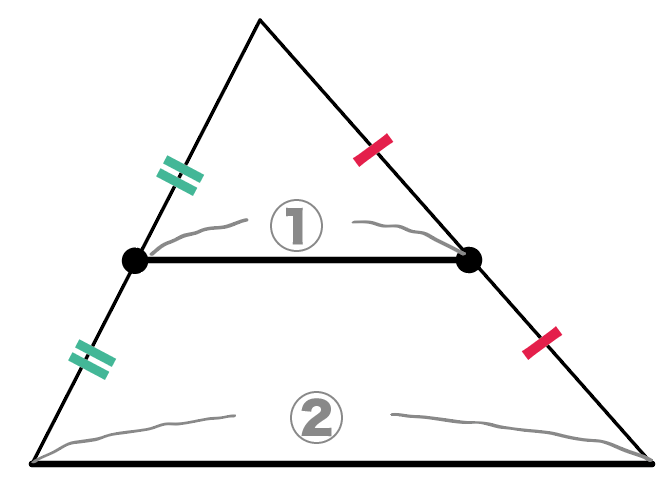
なおかつ、底辺と平行になっているんだ!
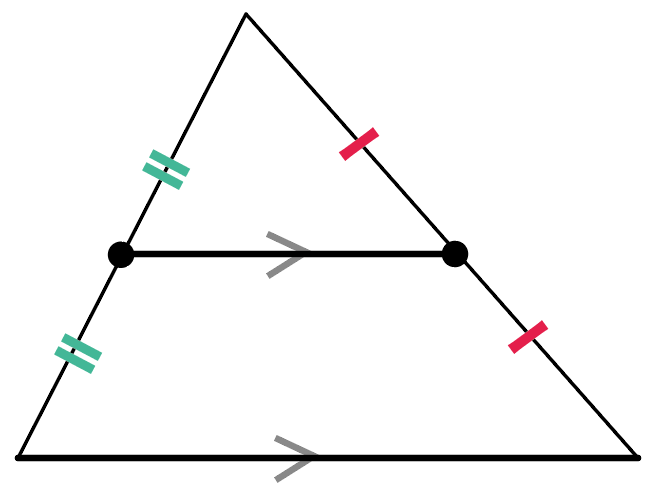
これが中点連結定理の正体。
つまり、中点連結定理の中身を開けてみると、おもに2つに分かれてるわけ。

三角形の中点を結ぶだけで底辺の半分の線が引けて、しかも、そいつは底辺に平行でもあるっていうんだ。
むちゃくちゃ楽チンな定理だね。
えっ。中点連結定理は役に立つのかって??
今日はそんな疑ってるみんなのために、実際に中点連結定理を使ってみよっか。
つぎの△ABCを想像してみて。
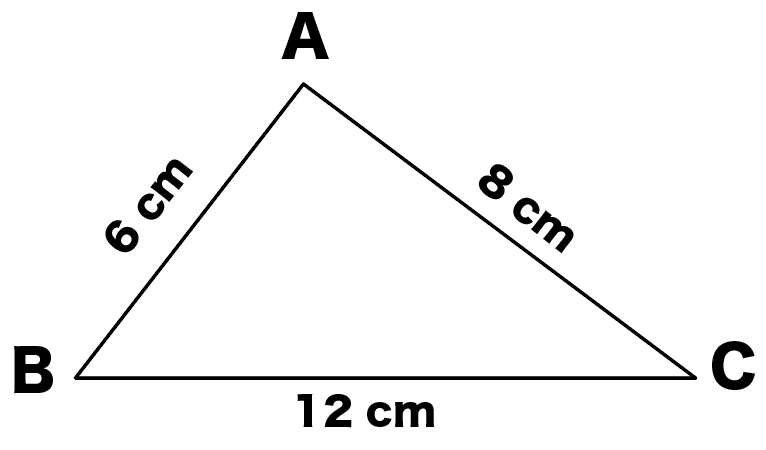
こいつの、辺 ABとACの中点 Mと Nを結んでみたんだ。
∠ACB=48°のとき、
を求めてみよっか!
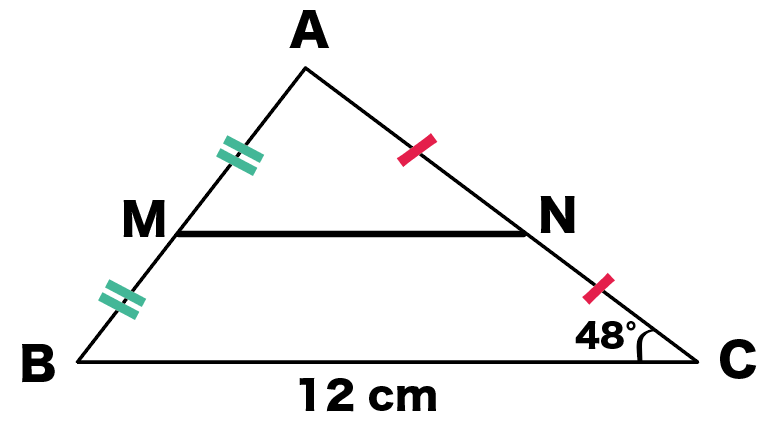
まずはMNの長さを求めてみよう。
MとNはそれぞれ三角形の辺の中点だから、さっき勉強した中点連結定理が使えるね。
中点連結定理では、三角形の辺の中点を結ぶと、
「結んだ線分の長さ」は「底辺の半分の長さ」になる
って習ったね?
だから、MNの長さは底辺BCの半分になるはずなんだ。
よって、
MN = 1/2 BC = 12×1/2 = 6cm
になるよ。
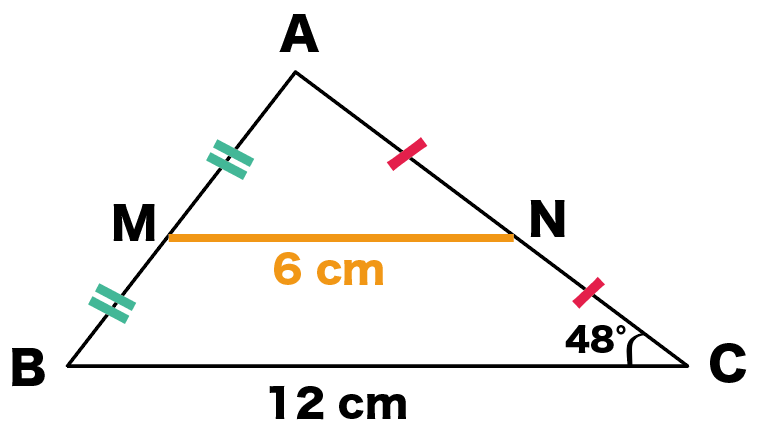
中点連結定理を使ってやると、中点を結んだ線分の長さを1秒ぐらいで計算できちゃうんだ。
ね?便利でしょ??
つぎは、∠ANMの大きさを求めてみよっか。
中点連結定理のもう1つの性質の、
三角形の辺の中点を結んだ線分は底辺に平行になる
を使うと求めることができるよ。
MとNは△ABCの辺のそれぞれ中点になってるよね??
だから、中点連結定理を使うと、
MN//BC
ってことがわかる。
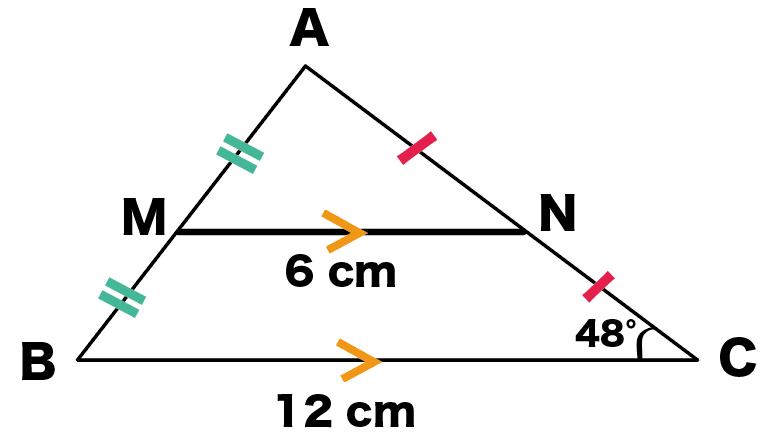
平行な線分同士の同位角は等しいから、同位角の位置にある、
は等しいはずなんだ。
問題によると、∠ACB = 48° だから、
∠ANM = ∠ACB = 48°
になるってわけ!
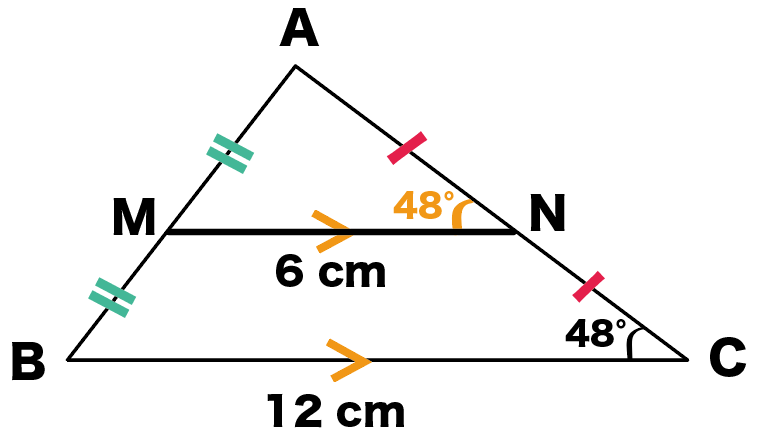
やったね!
これで中点連結定理の平行になる性質も使うことができた!
中点連結定理はどうだったかな?
最後にもう一回復習しておこっかー!
【中点連結定理】
三角形の2辺の中点を結ぶと、
結んでできた線分は、底辺の長さの半分になり、
しかも、底辺に平行である。

中点連結定理を使った証明問題はよく定期テストにも出てくるから、しっかりおさえておいてね。
そんじゃねー
Ken