こんにちは!この記事をかいているKenだよ。昼寝は好きだね。
連立方程式ってムズいよね。
加減法や代入法とかあるし、
方程式も2つあるからクラクラしてこない?。

今日はそんな「連立方程式の解き方」を徹底解説していくよ。
わからないときに参考にしてみて。
連立方程式の解き方では、
2つある文字を1つ消去する
ってことが基本になるよ。

えっ?なんでメンドクサイことするのかって??
それは、中1数学でならった
「一次方程式」の解き方を使うためさ!
知ってる解き方を使うために、文字を1つ消そうってわけ。
つぎの例題をみながら解説していくよ。
次の連立方程式を解きなさい。
2x+3y = 16
x + 7y = 19
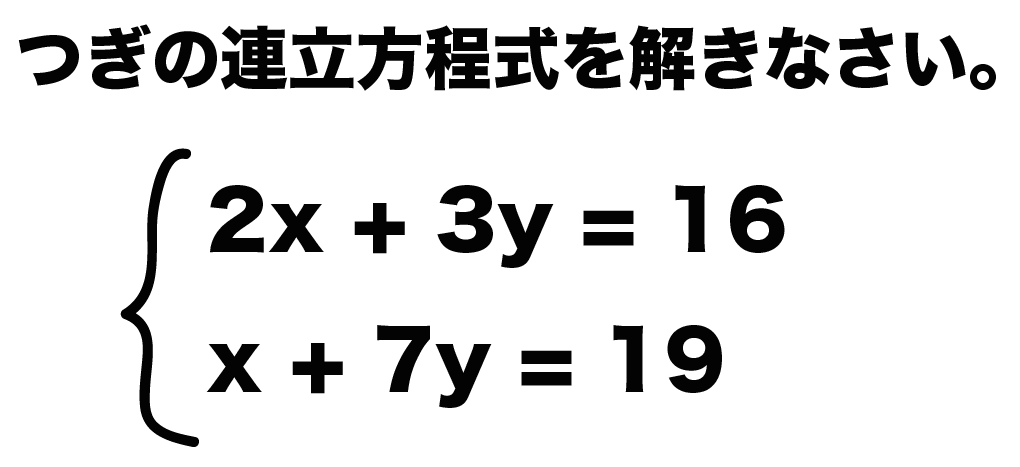
つぎの3ステップで連立方程式もイチコロさ。
連立方程式の文字を1つにしてあげよう。
どんな手を使っても構わない。
1つになれば、一元一次方程式になって解けるからね。

消去する方法はつぎの2つさ。
どっちの消去法を使うのか??
はぜんぜん自由。
だけど、だいたい「加減法」を使うことが多いね。
※連立方程式の解き方のコツ 参照
例題でも「加減法」で文字を消していくよ。
2つ目の式を2倍して1つ目の式からひいてやると、
xが消えるよね?

yだけの
-11 y = -22
っていう方程式になる。
一元一次方程式をといてあげよう!
解き方を忘れたときは「一次方程式の解き方」をみてみてね。
例題をみてみよう。
yの係数(-11)で両辺をわってあげると、
y = 2
っていう解がゲットできるよ。
あとはxだけだね!
解を代入してみよう。
代入する方程式はどっちでもいいよ。
簡単に計算できる式を選んでみて!
例題では、
x + 7y = 19
に「y =2」を代入してみたよ。

すると、
x + 14 = 19
x = 5
って感じでxの解もゲットできる。
これでようやく、
(x, y) = (5, 2)
と2つの解が得られたね。
おめでとう!!
連立方程式の解き方はどうだった??
の3ステップでいいんだ。
やり方がどうしても覚えられない!
ってときは問題をたくさん解いてみてね!
そんじゃねー!
Ken

連立方程式の解き方には2つある。
それは、
だったね。
連立方程式の解き方が2つもあって便利・・・
って思うじゃん?。
だけれども、
「加減法・代入法」のどっちを選んだらいいのかわからない
って戸惑っちゃうことが多いんだ。

今日は、そんな迷いをぶっ放すために、
連立方程式の解き方(加減法or代入法)をみわけるコツ
を紹介していくよ。
すっきりしたいときに参考にしてみて。
〜もくじ〜
まずやっぱり気になるのは、
加減法と代入法のどっちが多いのか??
ということだよね。
平等に「50:50」なのか??
もしくは、
超不平等に「1:99」なのか??
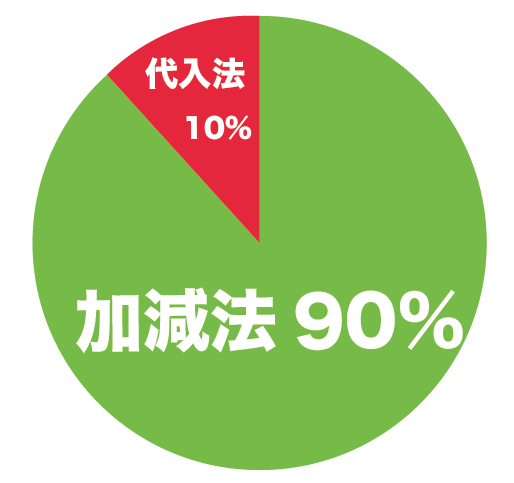
じつは、これは経験上の話になるんだけど、
連立方程式の約90%が「加減法」を使っているんだ。
つまり、
「代入法」を使うときってめずらしいんだ。
「代入法」ってめんどうだからね。 使いたくないのは当然のことさ。
「加減法」を使ったほうが簡単に解ける問題が多いんだよ。
連立方程式の解き方(加減法or代入法)を見分けるコツは、
代入法で解く特殊なケースを覚える
ってことさ。
これを覚えちゃえば、
特殊なケースに出くわしたら「代入法」、
ソレ以外は「加減法」で解けるよね!
代入法を使う特別なケースってつぎの2つのときが多いよ。
連立方程式の式で、
文字が片方によっている連立方程式
は代入法で解いたほうが便利なんだ。
しかも、よっている文字の係数が1ならなお最高!
たとえば次のような連立方程式の問題のときだね。
例題1. つぎの連立方程式を解きなさい。
$$2x+3y=11$$
$$y = 5x$$

この問題では、2つ目の方程式では「y」が左辺によっているよね??
こういう場合、
よっている文字をもう1つの方程式に代入するだけでいいから、
代入法のほうが簡単なんだよ!
問題文で「代入法で」連立方程式を解きなさい!
って命令されているパターンだ。
このときは指示に逆らわず、「代入法」で連立方程式をといてあげよう。
数学のテストでは問題文の命令はゼッタイだからね。
逆らってもろくなことがない。
たとえば、つぎのような問題のケースだ。
例題2. つぎの連立方程式を、代入法で解きなさい
$$2x+3y = 11$$
$$5x-9y =90$$
このパターンの場合、
どんなに「加減法」を使いたくても「代入法」で解かなきゃいけない。
おそらく、
解答用紙に「計算式」をかけ!
って要求してくるだろうからね。
問題文の命令はゼッタイ!
その道が険しくても・・・・ね!
連立方程式の解き方はだいたい「加減法」だよ。
困ったら加減法。
めんどかったら加減法。
迷ったら加減法。
いや、なんとなく加減法。

そんじゃねー
こんにちは!この記事をかいているKenだよ。カフェはやっぱいいね。
中学2年生になると、
二元一次方程式
を勉強するよね??
正直、聞いただけでもむずかしそうだし、数学が嫌いになっちゃいそうだ。

いや。
いやいや。
大丈夫。
そんなときはこの記事を読んでみて。
二元一次方程式の意味がしっくりするはずさ。
〜もくじ〜
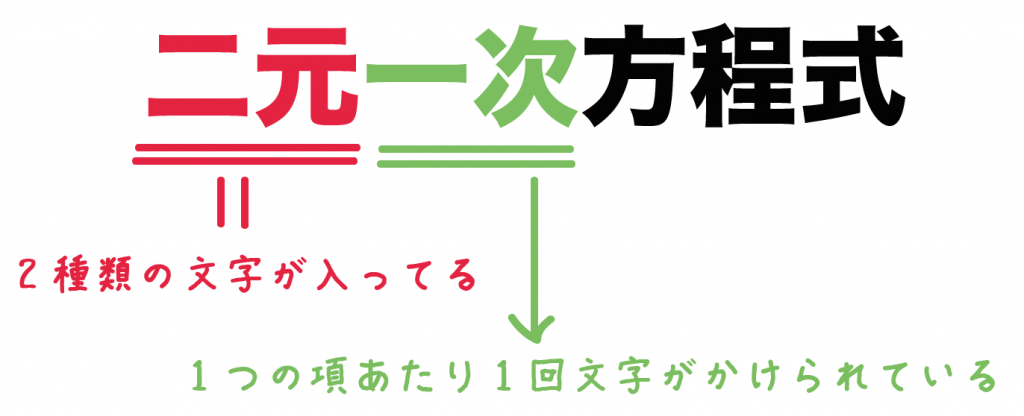
二元一次方程式って、
2種類の文字が使われている一次方程式のこと
なんだ。
もっと簡単にいうと、
2種類の文字が入っていて、1つの項あたり最大1回文字がかけられている方程式
のことなんだ。
たとえば、
2x – 5y = 26
とかね。

この方程式は、
xとyの「2種類」の文字が使われていて、
なおかつ、
1つの項に1回ずつ以下ずつ文字がかけられているからね。
じつは、
ってことを表しているんだ。
だから、
x + y + z = 90
っていう方程式は「三元一次方程式」だし、

2x + xy + z^4 – w = 90
っていう方程式は「四元四次方程式」になるのさ。

数学の先生に、
この方程式は何元何次方程式ですか??
ってきかれたら、
ということを見極めよう。
即答できればクラスの人気者さ!
二元一次方程式にも「解」があるよ。
方程式の「解」って、
文字に入れても等式が成り立つ「数字」のこと
だったよね。
たとえば、さっきの「2x-5y = 26」という二元一次方程式の解は、
・・・・・・・・・
などなど・・・2つ以上あるよね。
どうしよう・・!
解が1つじゃねえよ・・・・
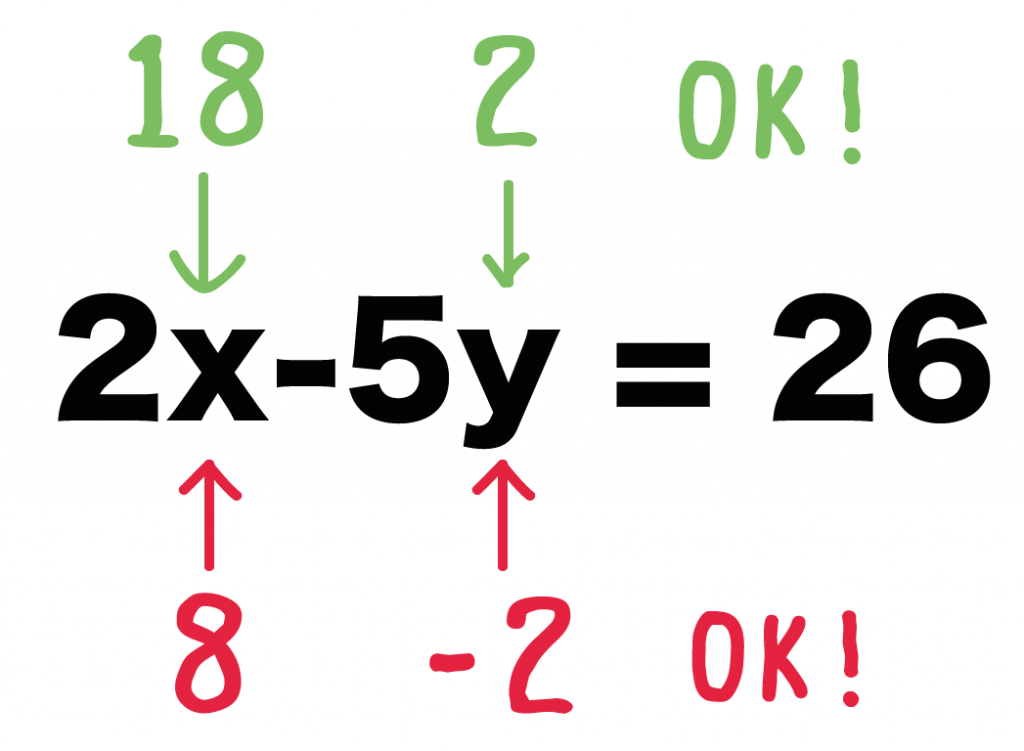
じつは、二元一次方程式1つだけでは解が1つに定まらないんだ。
二元一次方程式の解を求めるには、
2つ以上の二元一次方程式が必要だよ。
たとえば、
っていう2つの方程式があったら、
さっきの2つの解のうち、
しか成り立たなくなるよ。
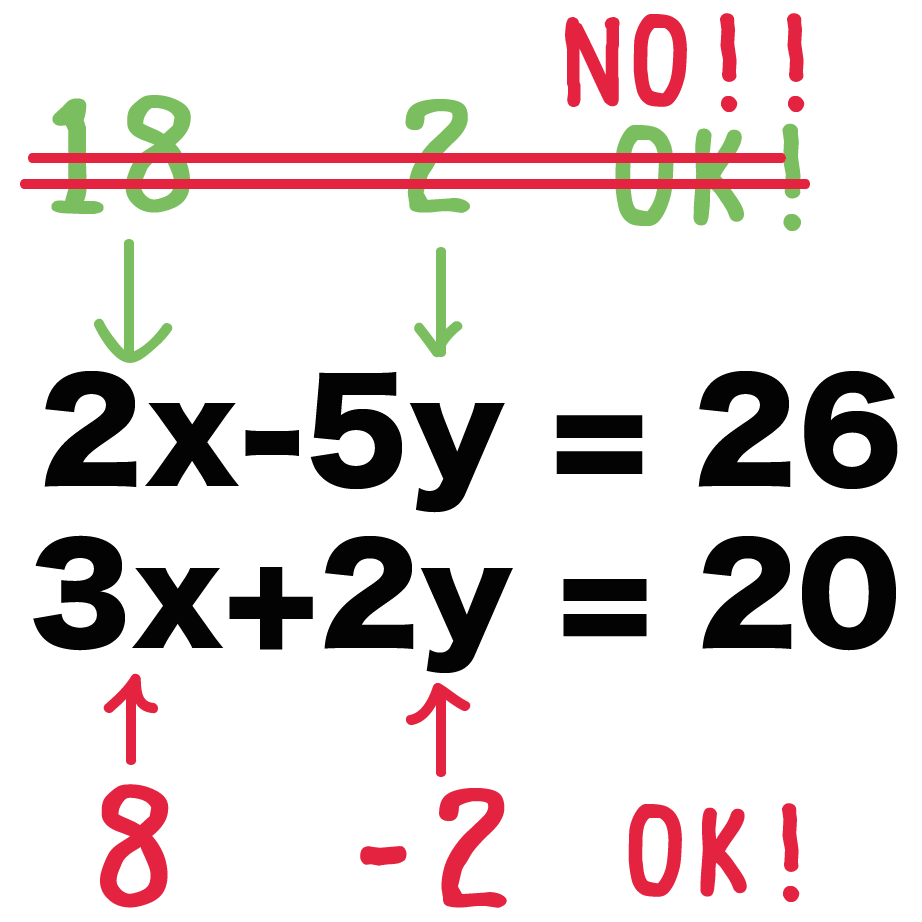
ってことで、
二元一次方程式の解を1つに決めたかったら、
2つの二元一次方程式を用意する
ってことをおぼえておこう。
このように、2つの方程式を組にしたものを「連立方程式」っていうんだ。
これから連立方程式をみっちり勉強していくよー!。
二元一次方程式って呪文みたいに聞こえるけど、
じつはシンプル。
2種類の文字が入った一次方程式のことなんだ。
もっと簡単にいってしまえば、
2種類の文字が入っていて、1つの項あたり最大1回文字がかけらている方程式
のことなんだ。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。うたたねが得意だね。
中2数学の「文字式の利用」はけっこうむずい。
ここでは、
文字式を利用して「すごいこと」をしなきゃいけないんだ。
ただ計算するだけじゃ許してくれない。
まったく、中2数学もきついね。

今日は、中2数学の山場ともいえる、
文字式の利用の問題の解き方
を3ステップで解説していくよ。
つまずいたときに参考にしてみてね。
文字式の利用の解き方はたったの3ステップさ。
例題をときながらみていこう!
2つの整数が、偶数と奇数のとき、その和は奇数になります。そのわけを説明しなさい。

問題文の「数字」を「文字」であらわしてみよう!
イメージでいうと、
「数字」っていう野菜を、
「文字」っていう包丁で切って「文字式」っていうカレーをつくるって感じw

えっ。ちょっと想像できないだって??w
それじゃあ例題をみていこう。

例題では「偶数」と「奇数」っていう2種類の数字がでてきたね。
こいつらを文字で表現してやればいいのさ。
m、nを整数とすると、
と文字式ができるね。
だって、偶数は2で割り切れる数だからね。
ってことは、ある整数を2倍した数ってことになるでしょ??
また、奇数は「偶数に1を足した数」だから整数を2倍して1を足せばいいんだ。
これで偶数と奇数という「数字」を、
m・nという「文字」であらわせたね。
文字式を使って指示されたことをやってみよう。
文字式の利用では、必ず、
数字の文字式をつかって何かしてみて??
っていうメッセージが込められているんだ。
よーく問題文を読み返してみよう!

問題文を読み直してみると、
「その和は奇数になります」
っていう文にメッセージが隠されていない??
そう。
そうなんだよ。
この文章では、
「偶数」と「奇数」を足してみて??
っていうダイイングメッセージが込められているんだ。
コナンでもきっと読み取ってくるだろう。
つまり、この問題では、
「偶数」と「奇数」をたして「奇数」になるよー
ってことをいってあげればいいんだ。
だから、まずはその2つをたしてやるのさ。
実際に「偶数(2m)」と「奇数(2n+1)」をたしてやると、
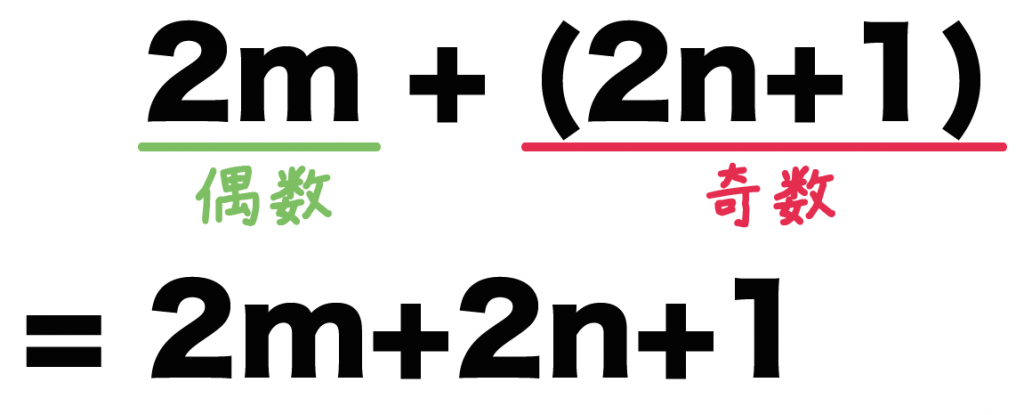
2m + (2n+1)
= 2m+2n+1
になるね!
あとは問題文の「ゴール」に力技で着地するだけさ。
問題文をよーく読んで、
何をすればゲームクリアなのか??
ということを見極めよう!
たいてい、メッセージ後に「ゴール」が潜んでいることが多いよ。
例題の文章をもう1度読んでみよう。
すると、
「その和は奇数になります」
という文から、
「偶数」と「奇数」の和が「奇数」になること
がゴールだと読み取れるはずだ。

つまり、
偶数と奇数をたしたら奇数になる!
って言ってやれば問題でマルがもらえるってわけさ。
奇数ってことは、
整数×2+1
になってればいいよね??
2m + 2n +1
という文字式のmとnを係数2でかこってあげると、
2(m+n) +1
になるね。(m+n)は「整数+整数」で「整数」になるから、
2(m+n) +1 は「奇数」
ってことがいえるんだ。
これで、問題のゴールの、
「偶数と奇数の和は奇数になる」
ってことがいえたわけ!
おめでとう。
これで文字式の利用の解き方もゲットだね!
文字式の利用の解き方は、
の3ステップだったね。
この中でもっとも重要なのは、
問題文からゴールをみつける
ということ。
これさえできれば、どんな文字式の利用の問題でも大丈夫!
問題に慣れてテストをむかえてみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。家具の匂いが好きだね。
文字式の計算でいちばんむずかしいことって、
分数の通分
だよね。
分数だけでヤッカイなのに、それが文字になる?!?
たまったもんじゃない。

そこで今日は、
分数の文字式の通分方法
を3分で解説するよ。
通分がどうしてもできねえ!ってときに参考にしてみて。
〜もくじ〜
文字式の分数の通分方法を勉強する前に、
分数の通分ってなに??
ということを確認しよう。
これがわかってないと文字式の通分どころじゃないからね。
通分って、
2つ以上の「分母の違う分数」を1つにすること
なんだ。

これが分数の通分っていうものさ。
たとえば、
1/2 + 1/3
っていう分数式を通分して1つにしてやると、
5/6
になるんだ。
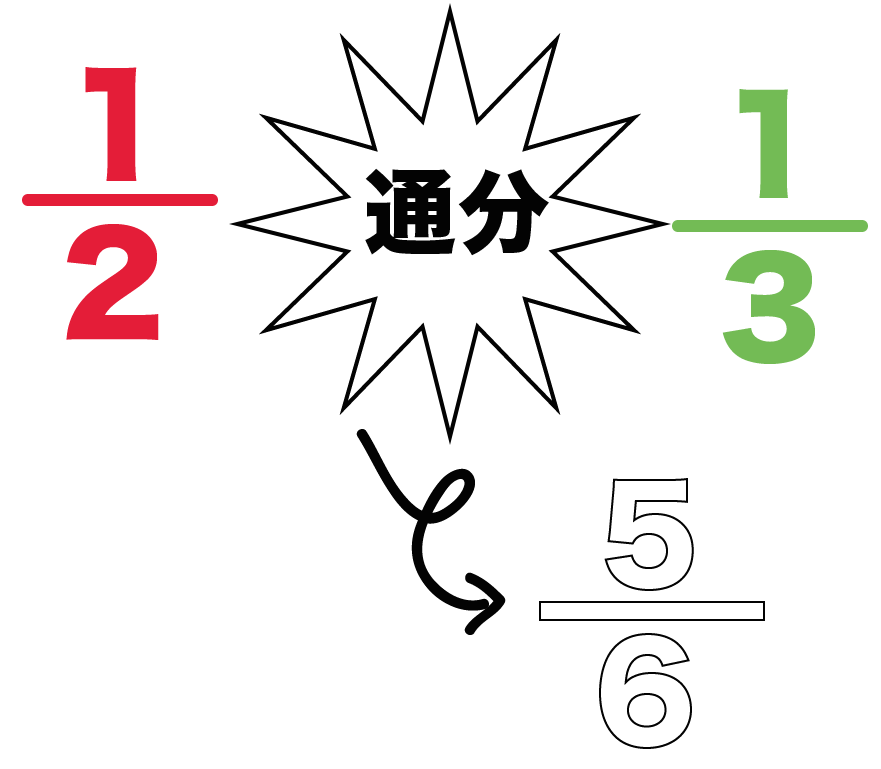
これを文字式の分数でもやっていくってわけさ。
分数の文字式を通分する方法は、
っていう2ステップだ。
分子と分母を順番に計算すればいいってことだね。
つぎの例題をときながら通分をマスターしていこう!
つぎの分数の文字式を通分して1つにしなさい。
2b/a – 5d/c

まずは通分後の分母をきめちゃおう。
通分後の分母は、
分母をかけあわせたもの
なんだ。
例題の計算式の2つの分母は、
だったよね??
こいつらをかけあわせてやればいいんだ。
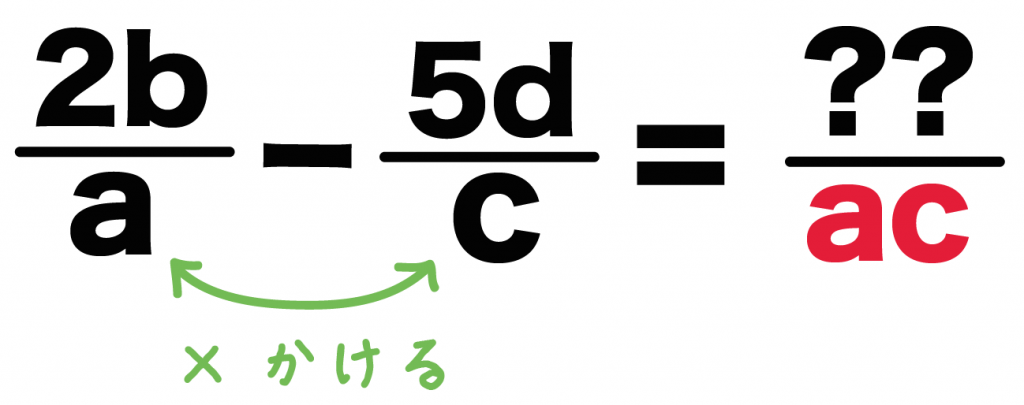
その答えが通分した分母になるってわけ!
あとは分子だ!
通分後の分子の計算方法は、
たすきがけ
というものさ。
「自分の分母」と「相手の分子」をかけたものを足し合わせればいいんだ。
ななめに掛け合わせるようすが「駅伝のたすき」に似てるから、
「たすきがけ」って呼ばれているんだ。
例題でいうと、
っていう計算をして、そいつらを足してやればいいんだ。
足したものが通分後の「分子」になるのさ。
それぞれ計算してやると、
になる。そんで、そいつらをたしあわせてやると、
2cd-5ad
になるよね。こいつが通分後の分子になるわけさ。
ってことで、
最終的に例題の分数を通分すると、
(2bc-5ad)/ac
になるよー!
おめでとう。 これで文字式の分数の通分もマスターできたね!
分数の文字式の通分はどうだったかな??
っていう2ステップで簡単に計算できちゃうはず。
中学数学の基礎だから、ここでマスターしておこうね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。10円玉募金をはじめたね。
分数がふくまれる「等式の変形」ってむずかしいよね。
整数だけでもヤッカイなのに、分数がはいったらもっとヤバい。
そこで今日は、
「分数がふくまれている等式の解き方」をわかりやすく解説していくよ。
分数がふくまれる「等式の変形」には2つのパターンがあるんだ。
まず1つ目は分母を払うパターンだ。
これは「求める文字」が分子にあるタイプだね。
たとえば、
つぎの等式をaについて解きなさい。
a/2 + b/5 = 2
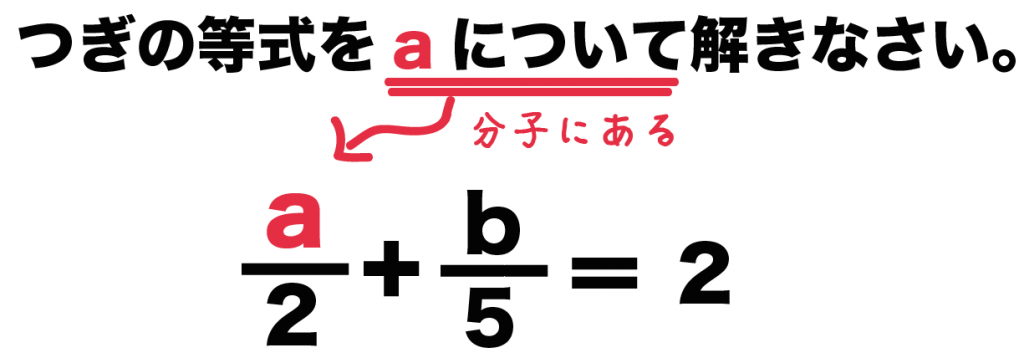
っていう問題だ。
これは、
○○について解きなさい
っていう○○の文字が分子にはいっているよね。
このタイプの問題はつぎの3ステップでとけちゃうんだ。
まず分母をはらっちゃおう。
等式から分数を消せちゃうってわけ。
つまり、
分母の最小公倍数を等式全体にかけてやればいいのさ。
例題でいうと、
分母の「2」と「5」の最小公倍数は「10」だよね。
こいつを等式の両辺にかけてみると、
10×(a/2 + b/5) = 2 × 10
5a + 2b = 20

になるね!
分母をはらった??
そのつぎは移項だね。
「求めたい文字」を左辺に移動させよう!
それ以外は反対の右辺におしこんでね。
例題でいうと、
等式で求める文字は「a」だったよね??
ってことは「a」をふくむ項を左に、ソレ以外の項を右によせてやろう!
すると、
5a + 2b = 20
5a = 20 -2b
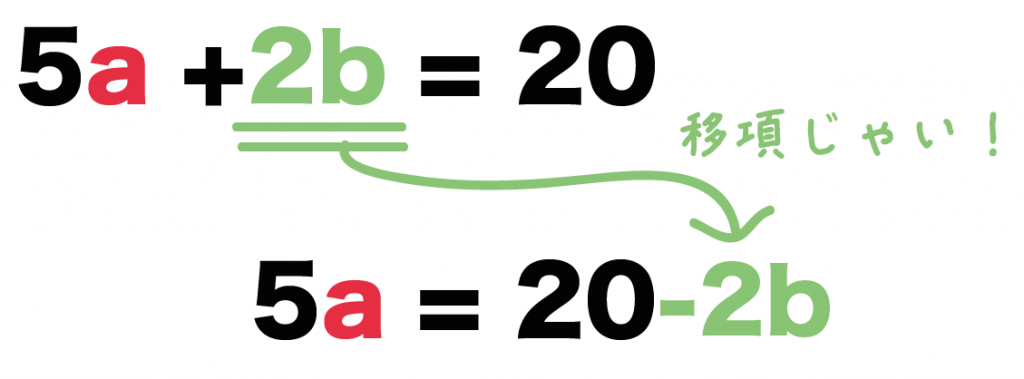
になるね!
移項するときに、項の符号が変わることに注意してね。
最後は「求める文字」の係数をとってあげよう!
求める文字の前についている「数字」が係数だよ。
こいつで両辺をわってあげよう!
すると例題の式は、
5a ÷ 5 = (20-2b) ÷5
a = (20-2b)/5
になるね!
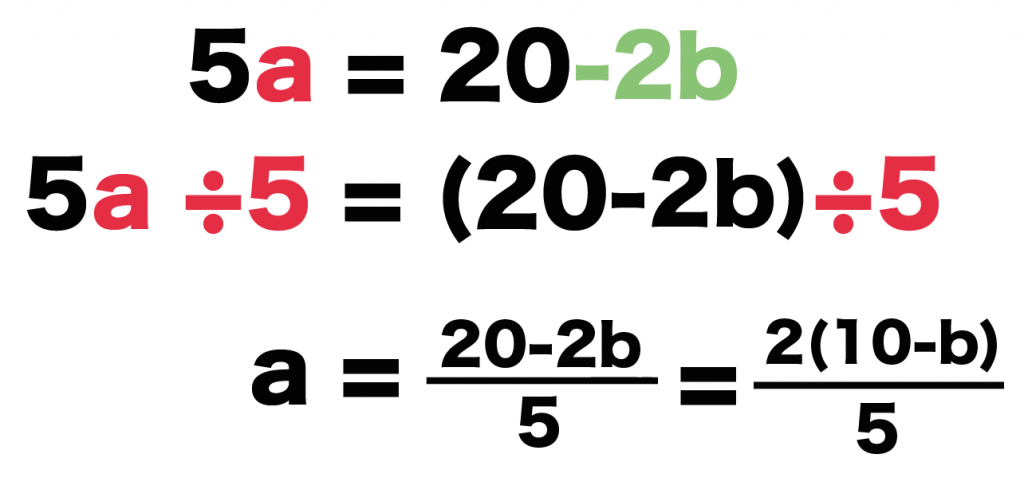
これで分母をはらうやり方はオッケーだね!!
等式の変形の2つ目のパターンは、
「求める文字」が分母にある場合だ。
たとえば次の問題のように、
つぎの等式をaについて解きなさい。
1/a + 1/b = 1/c
「〜について解きなさい」の「〜」が分母にはいっちゃっているパターンだ。
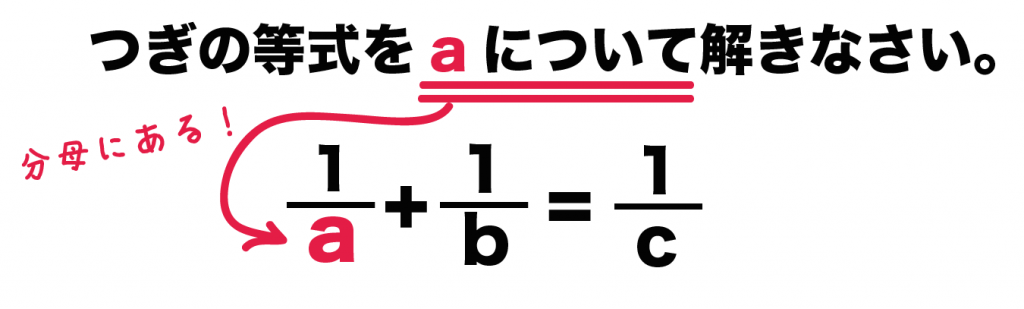
このタイプはつぎの3ステップでとけちゃうよ。
「求める文字」を左辺に、ソレ以外の項を右辺によせちゃおう!
符号に注意して移項しちゃってくれ!
例題の等式では「a」が求める文字だったよね?
だから「a」を左辺に、ソレ以外の項たちを右辺によせてみよう。
すると、
1/a = 1/c -1/b
になるね!
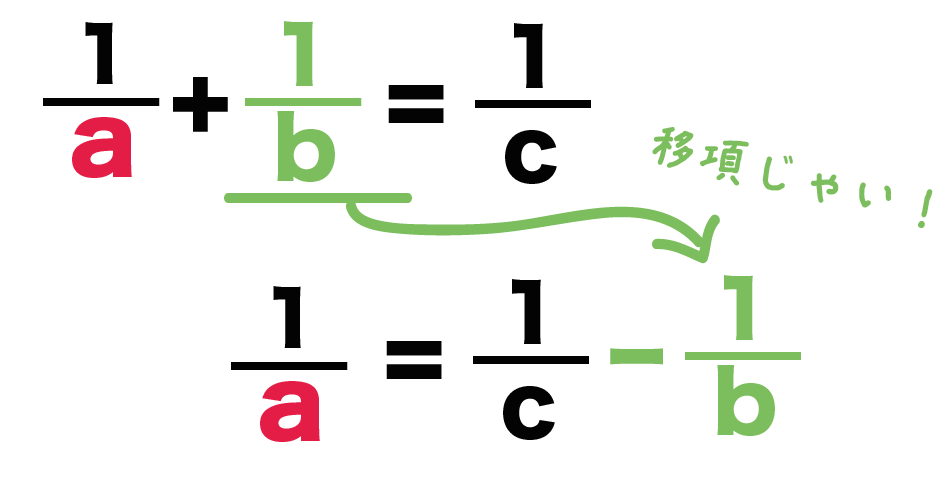
右辺を通分して1つの分数にしてみよう!!
例題でいうと、
1/c -1/b
っていう右辺を通分してやればいいんだね。
えっ。通分のやり方がわからない!?
そんなときは「分数をふくむ文字式の通分方法」を復習してみてね。
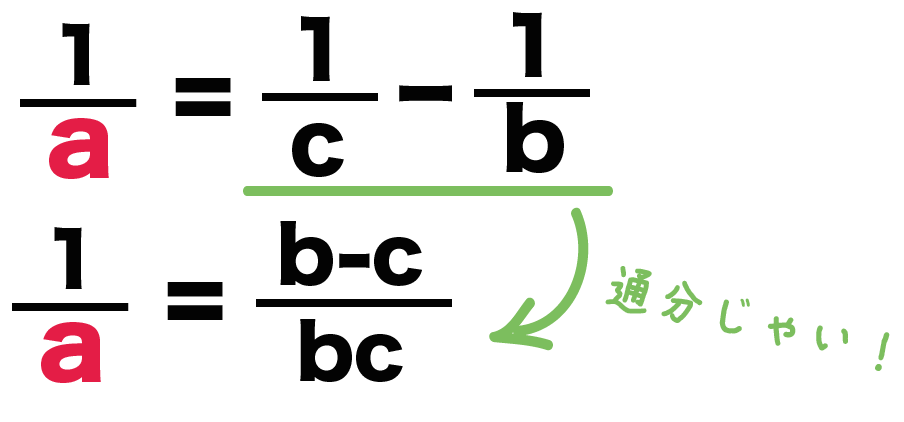
通分してやると、
(b-c)/bc
になるね!
いよいよ最後のステップ。
両辺の分数を逆数にしてあげよう!!
左辺と右辺はそれぞれ1つの分数になっているから、
分子と分母を入れ替えてやればいいのさ。
例題でいうと、
1/a = (b-c)/bc
a = bc/(b-c)
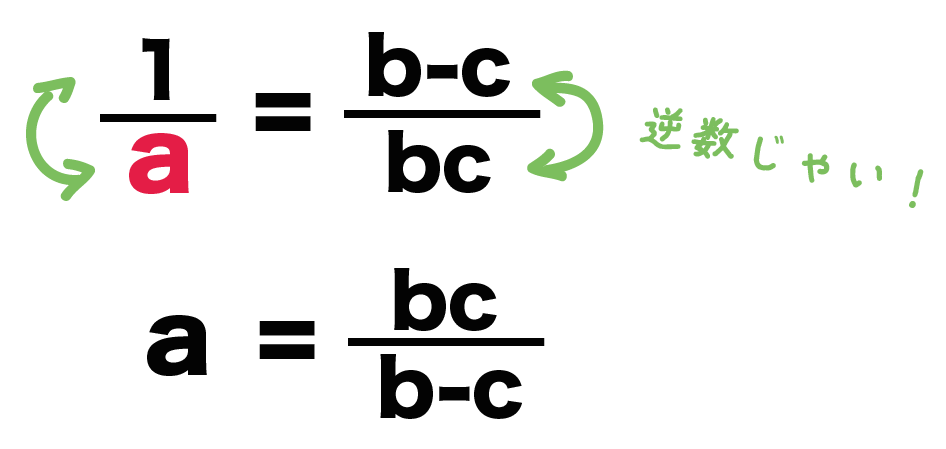
になるね!
これで「通分するパターン」の解き方もマスターしたね。
おめでとう!
分数がふくまれている等式の変形のやり方はどうだった??
をマスターしておけば大丈夫。
きっとテストでいい点とれるはず!本番前によーく復習しておいてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。もやしは安いね。
等式の変形のやり方がわからない・・・・
ってときあるよね??
うん、わかるよ。その気持ち。
だって、等式の変形なんて見た目がむずかしそうだよね。
しかも、等式の変形なんてなくても生きていけるからね。できれば避けたいはずだ。
今日は、そんな「等式の変形」の問題を3秒ぐらいでとける解き方・やり方を伝授するね。
つぎの練習問題をときながら解き方をみていこう。
練習問題
つぎの等式を[ ]内の文字について解きなさい。
12a + 5b = 2 (4a-1) [a]

等式の変形はつぎの3ステップでとけちゃうんだ。
等式を分配法則をつかってカンタンにしてみよう。
例題でいうと、右辺の2(4a-1)の()をはずすことができるよね??

分配法則で計算してやると、
12a + 5b =2(4a-1)
↓↓
12a + 5b =8a -2
になるよ。
等式の変形の問題では「メイン文字」に注目しよう。
メイン文字とは、
〜について解きなさい
という「〜」の部分にあてはまる文字のこと。
つまり、「aについて解きなさい」っていう問題は「a」が「メイン文字」になるってわけ。

このステップでは、
メイン文字を左辺によせる
ってことをしよう。
ぶっちゃけ右でも左でもいいんだけど、左に寄せたほうが解きやすいからね。
メイン文字以外の項は右辺によせてね。

例題でいうと、
aがメイン文字だよね? だって「aについて解きなさい」って言ってるからね。
aがついている項を左辺によせればいい
ってことさ。
12a + 5b = 8a -2
という等式で、aがついている項を左辺に、それ以外の項を右によせてみよう。
すると、
12a – 8a = -2 -5b
になるね!

そんで、この等式の両辺の同類項をまとめてやると、
4a = -2 – 5b
になるね!
メイン文字の係数で両辺をわってあげよう。
つまり、
メイン文字をちょっとスリムにしてやるってことさ。
コイツはちょっと太りすぎてるからね。
係数でわってメイン文字だけを残してあげよう。
例題のメイン文字の係数は「4」だよね??
こいつで両辺をわってあげよう。

4a = -2 – 5b
の両辺を「4」でわってやると、
a = (-2 -5b)/4
になるね!
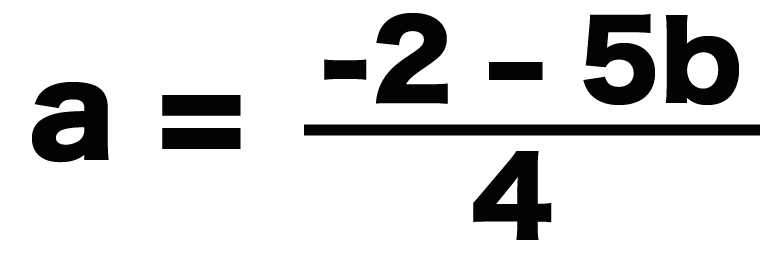
むちゃくちゃ左辺がすっきりしたっしょ?? だって、メイン文字しか残ってないからね。
これでこの例題の等式は、
aについて解けた!
ってことになるよ。
おめでとう!!これで等式の変形も完ぺきだね。
等式の変形は意外とシンプル。
〜について解きなさい、
の「〜」の文字を左辺によせて両辺を係数でわるだけ!
中1数学で勉強した「移項」さえマスターしておけば大丈夫さ。
等式の変形はテストに出やすいから、解き方をよーく復習しておいてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。焼き肉はうまいね。
中2数学のテストでいい点をとるためには、
いろいろな多項式の計算方法
をマスターしておくべきなんだ。
だって、中2数学の基礎的な内容だからね。
多項式の計算の攻略なしにして、中2数学の攻略なし、
ってわけさ。
今日はそんな中2数学のカギをにぎる「多項式の計算」の問題の解き方を
3ステップで紹介していくよ。
よかったら参考にしてみて。
例題をときながら多項式の計算方法をみていこう!
例題:
つぎの計算をしなさい。
2(a+3b+c)-3(2a+5b+3)
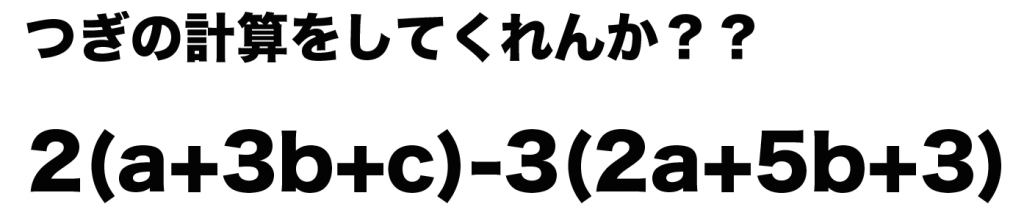
つぎの3ステップでいいんだ。
分配法則をつかって多項式の()をはずしちゃおう!
()がついている多項式ってぽっちゃりしてるっしょ?
だから、こいつをスッキリさせちゃうってわけ。
例題の多項式も()が2つあるよね。
この邪魔くさい()を分配法則ではずしてやると、

2(a+3b+c)-3(2a+5b+3)
= 2a+6b+2c-6a-15b-9
になるね!
−の符号に注意しながら()をはずしてみてね。
スッキリした多項式の中から、
同じ文字の項(同類項)
をみつけてみよう!
aが使われている項、bが使われている項・・・というように文字ごとに洗い出していけばいいんだ。
例題をみてみると、
分配法則でカンタンにした多項式(2a+6b+2c-6a-15b-9)には、
っていう4種類の項があるよね??

こいつらがそれぞれ何個ずつあるかってことを押さえておこう!
さっきみつけた「同じ文字の項(同類項)」の係数を足し合わせてみよう。
あ、係数って文字の前についている数字のことだよ。
例題の多項式では、
という2種類の文字が2つ以上ふくまれていたよね?
ってことはコイツらの係数を足してやればいいわけさ。
すると、
2a+6b+2c-6a-15b-9
= -4a -9b +2c -9

になるね!
これで多項式の計算は終了さ。おめでとう!!
多項式の計算問題は、
っていう3ステップで攻略できちゃうんだ。
これさえ押さえておけば中2数学の基礎はできたようなもんさ。
テスト前にもう一度復習してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。カラオケもいいね。
中2数学でh「式の値」っていうやっかいなヤツがでてくる。
「式の値」の問題って、
文字式の中の「文字」に数字をいれたときの値を求める
っていうやつなんだ。
文字に数字をいれて計算するだけ!
慣れれば簡単だからガンガン点をとっていこう。
今日は中2数学ででてくる、
「文字が2つ以上登場する」式の値の問題
を解説していくよ。
よかったら参考にしてみて。
さっそく「式の値」の解き方をみていこう。
つぎの例題をといてみよう!
a = 3/2、b = -2/17のとき、次の式の値を求めなさい。
(8a + 3b) -2(3a-7b+1)

この手の問題は3ステップでちょちょいのチョイさ。
文字式を簡単にしてあげよう!
チョー簡単な式はそのままでいいんだけど、
()のついた式はもう少しシンプルにしちゃおう。
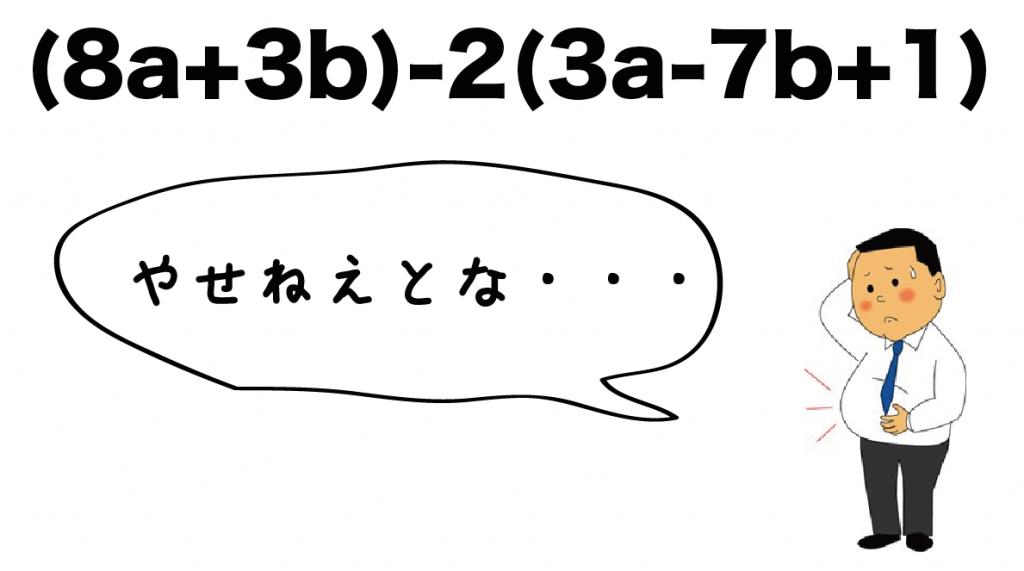
例題の文字式をみると、
(8a + 3b) -2(3a-7b+1)
って感じで()で文字式が太っているよね??
とてもじゃないけどスリムなんかじゃない。
(8a + 3b) -2(3a-7b+1)
をスリムにするために分配法則をつかってあげよう。
すると、
(8a + 3b) -2(3a-7b+1)
= 8a + 3b -6a + 14b -2
になるね!
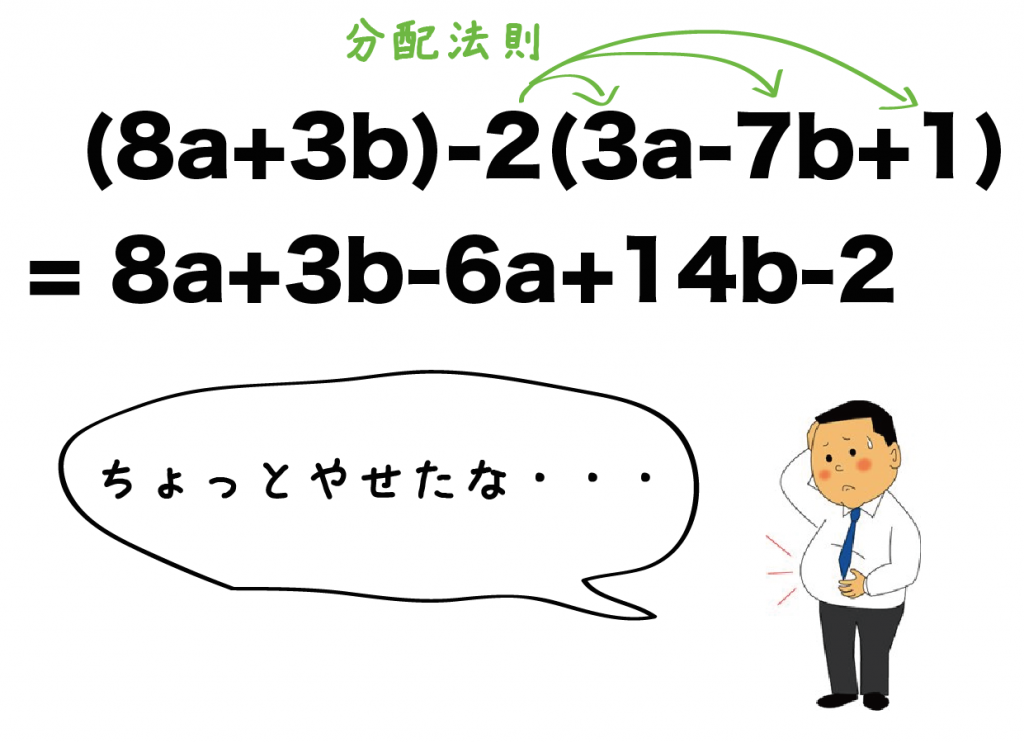
どう??だいぶスリムになったよね?。
文字式の()をはずしただけじゃまだスリムじゃない。
式は横に長いし、どうにかしてあげたくなるよね?。
つぎはもっとシンプルにするために、
同類項をまとめる
っていう荒技で勝負してみよう。
例題でちょっと簡単にした、
8a + 3b -6a + 14b -2
という式にはつぎの3種類の項があるよね?
同じ文字の項は係数をたしてみよう。

すると、
2a +17b -2
って感じで文字式がスリムになったでしょ??
最後に文字に数字を代入してみよう。
どんな数字を入れればいいのか
ってことは問題にかいてあるよ。
この例題では、
って問題で指定されているよね?
こいつらをStep2で計算した超スリムな文字式に代入してあげよう。
すると、
2a +17b -2
= 2 × 3/2 + 17×(-2/17) -2
= 3 + (-2) -2
= -1
っていう式の値が求まるね!
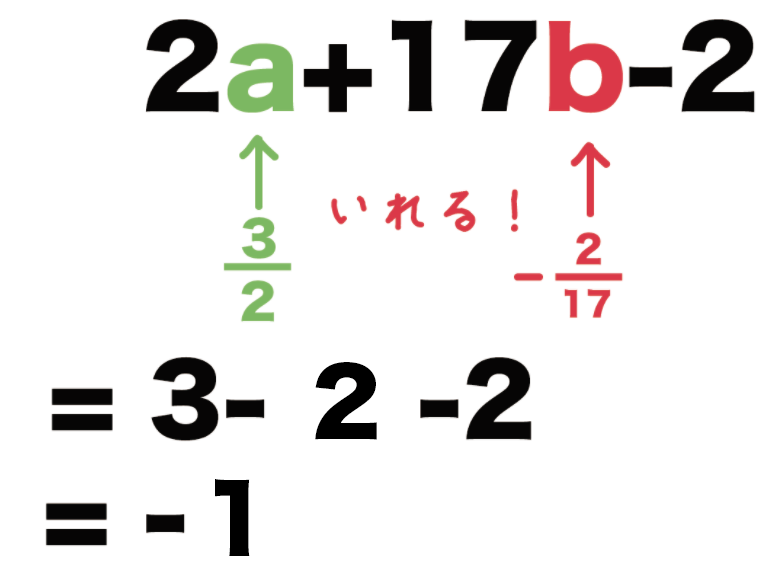
おめでとう。これで「式の値」もマスターしたね。
式の値を求める前には必ず、
文字式をできる限りカンタンにする
ってことを忘れずにね!
これなら焦らずに式の値を計算できるはず!
テスト前にもう一度復習してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。我が家にたんすが来たね。
「同類項」って、
「文字」と「次数」が同じ項たちのこと
なんだ。
つまり、
同じ英文字を使っていて、なおかつ、その文字が何回かけられているかが一緒
の項たちってことさ。
たとえば、
a²-2a-3a+4
っていう多項式があったとしよう。
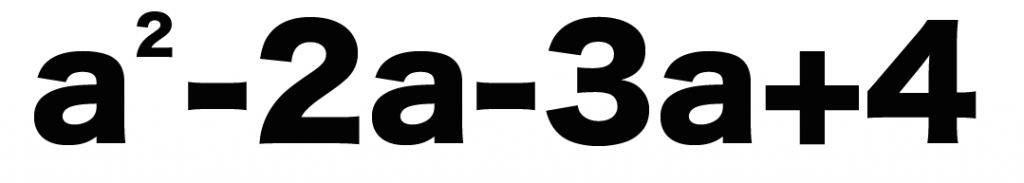
この多項式にはぜんぶで4つの項があるけど、
「文字」と「次数」が同じなのは次の2つだね。
この2つの項が同類項ってことになる。

そんで、中2数学の「式の計算」っていう単元では、
同類項をまとめる
っていうワザをマスターしていないといけないんだ。
今日はその「同類項のまとめ方」をわかりやすく3ステップで解説していくよ。
同類項がどうしてもまとめられん!ってときに参考にしてみてね。
「同類項をまとめる」ってつまり、
2つ以上の同類項を1つの項にするってこと
だ。
その「同類項のまとめ方」は3ステップでできちゃうんだ。
つぎの例題をときながらみていこう。
つぎの式の同類項をまとめてね。
2a + 7b – 2a² + + 8c + a³ – 6a²
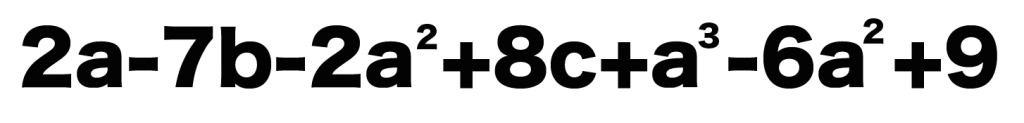
まずは同じ「文字」が使われている項をさがしてみよう。
つまり、同じアルファベットの文字をみつけるってわけ!
あ、数字の項は「数字」っていう文字だと思っていいよ。
例題の、
2a + 7b – 2a² + + 8c + a³ – 6a²
を3秒ぐらいみつめていると、
っていう4つの項に同じ「a」っていう文字が含まれていることに気づくよね。

だから、まずはこいつらが、
同類項である疑いが高い項たち
ってことさ。コナンでいえば、いかつくて犯人っぽいキャラみたいな感じだね。
つぎは「次数」が同じ項だけを抜き出してみよう!!
「次数」が同じってことは、
その文字がかかっている回数が同じ
ってことだね。つまり、
何乗されているか?ってことが一緒ならいいんだ。
例題をみてみよう。
さっきの「同じ文字の項たち」のうち、次数が同じやつは、

の2つだね。こいつらは文字も一緒だし、次数も同じだ。
だから同類項ってわけ!!
最後に、同類項たちをまとめちゃおう。
まとめ方はいたって簡単。
同類項の係数を足し合わせるだけでいいんだ。
係数って「文字式」の「文字じゃない部分」
のことだったよね??
例題をみてみよう。
っていう2つの項の係数はそれぞれ、
だ。こいつらを足しあわせてやると、
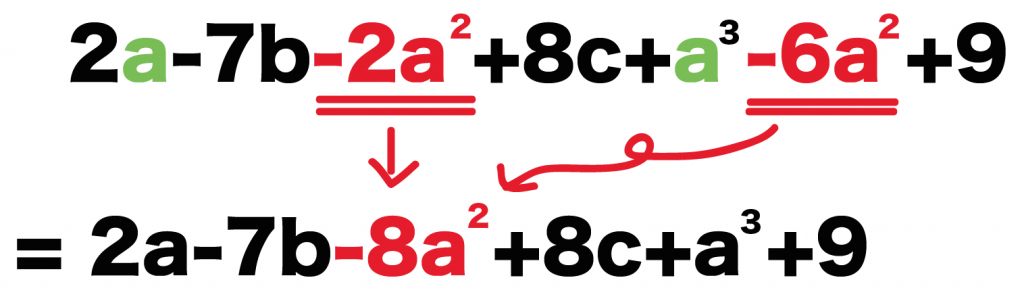
-2 + (-6) = -8
になるはず!!
係数じゃない文字の部分はそのままにしていいので、
例題の式の同類項をまとめると、
-8a²
になるね。
おめでとう!これで同類項をまとめられたね。
同類項のまとめ方はどうだった??
っていう3ステップで完了なんだ。
テスト前にもう一度確認してみてね。
そんじゃねー!
Ken

中2数学の「式の計算」で押さえたいことは、
「単項式」と「多項式」の違い
だね。この2つはごっちゃにしやすい数学用語なんだ。
だって、「単項式」と「多項式」って漢字で1文字しか違わないし、

ひらがなに直しても1文字違いだからね。

当然、勉強していると、
単項式と多項式をごっちゃまぜにする
という事態におちいるわけさ。
今日は、そんなミスをなくすために、こんな記事をかいてみたよ。
その名も、
3分でわかる!単項式と多項式の違い
さ。「単項式」と「多項式」の違いがわからないときに参考にしてみて。
「単項式」と「多項式」ってどっちも、
「文字」と「数字」でできた式
のことなんだ。

それで、こいつらにはこんな違いがあるんだ。
つまり、
「かけ算」だけできた文字式は「単項式」、
「かけ算」と「たし算」で成り立つ文字式は「多項式」ってことになるね。

それじゃあ、単項式と多項式をそれぞれ詳しくみてみよう!!
改めてもう一度復習だね。
単項式って、
「かけ算のみ」で表される「文字」と「数」の式のこと
なんだ。
たとえば、「5a」っていう式は単項式だね。

なぜなら、
「5」という数字と「a」っていう文字が「かけ算のみ」でつながっているからね。
また、文字だけの「p」っていう式も「単項式」だし、
数字だけの「5000」っていう式も単項式だ。
だって、なにもかかっていないように見えても
「1」がかけられているからね。
足し算が含まれていなければ単項式になる
ってことを覚えておこう!
多項式とは、
「かけ算」と「足し算」でできた「文字と数字の式のこと」
を言うんだ。
たとえば、
2a+7

とか、
a^2 + 3abc + 7
とかね。

もっといっちまえば、
単項式を+でつなげたもの
ともいえる。

だって、多項式の中の1つ1つの項は単項式になっているからね。
さっきあげた例でいうと、
「a^2」「3abc」「7」はすべて単項式
だね。

単項式を足し算で結ぶもの。
それが多項式だ!!
ただ、1つだけ多項式で注意すべきことがあるんだ。
それは、
「引き算」が含まれている文字式も多項式
ってことさ。
たとえば、
7a -9
なんかね。その理由は、
「-」は「-の項をたす」って解釈できるからだよ。

引き算ではなく、「−の項」を足しているってすればいいんだ。
−が含まれる単項式の集まりも多項式である
ってことを忘れずにね。
単項式と多項式の違いはどうだったかな??
発音はすげえ似てるけど、
単項式と多項式は「たし算」を含むかどうかが違う!

って覚えておこう。
そんじゃねー!