【三角形の比】角の二等分線の定理・性質の問題の解き方がわかる3ステップ

三角形の角の二等分線の定理をつかった問題わからん！

こんにちは！この記事を書いてるKenだよ。ナンは1つでいいね。

三角形の角の二等分線の定理・性質

っておぼえてるかな？？

念のために復習しておくと、

「三角形の二等分線と底辺の交点」と「各頂点の長さの比」が、他の辺の2辺と等しい

っていう定理だったよね？？

言葉じゃわかりづらいから図をみてみよっか。

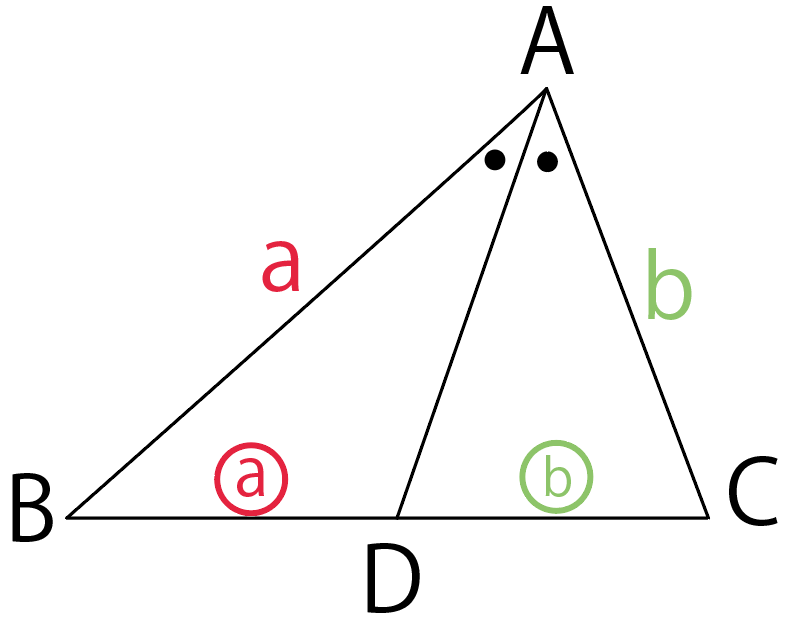
たとえば、

AB = a
AC =b

の△ABCで、∠Aの二等分線との交点をDとすると、

AB : AC = BD : DC = a : b　になってるんだ。

なぜ、三角形の角の二等分線の性質が使えるのかわからない？？

そういうときは、角の二等分線の定理の証明の記事を読んでみてね。

tomo

2016.09.22

三角形の角の二等分線の性質・定理の証明がわかる5ステップ

https://text.tomo.school/triangle-bisector-proof

三角形の角の二等分線の性質の証明？？ある日、数学が苦手なかなちゃんは、三角形の角の二等分線の定理の証明に出会いました。以下の図で∠BAD＝∠CADのとき、AB：AC = BD：DC であることを証明しなさい。証明なんか、嫌いだ！何で？文章書くのむずい。。確かに。でも、数学の証明もやっぱり数学なんだ。へっ？どこが？うーん、スタートとゴールが明確なとこかな。例えば計算問題だと？問題を解くと、答えにたどり着くってこと？そう、証明も同じ。証明することを見つけるのがスタートで、証明できたらゴール！ってこ...

今日はこの定理を使った問題を解説していくよ。

三角形の角の二等分線の公式をつかった問題の解き方3ステップ

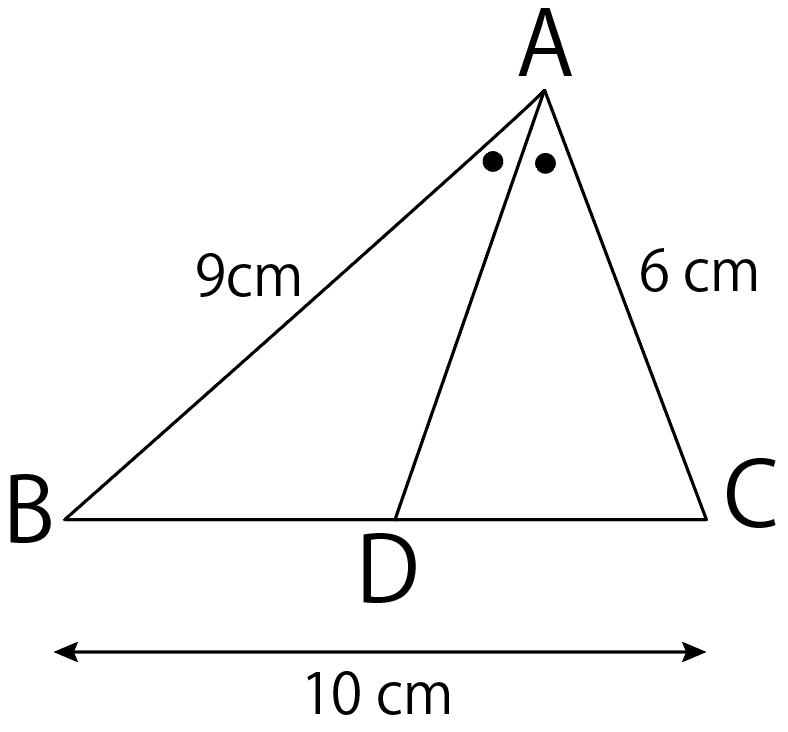
つぎの問題を解いてみよっか。

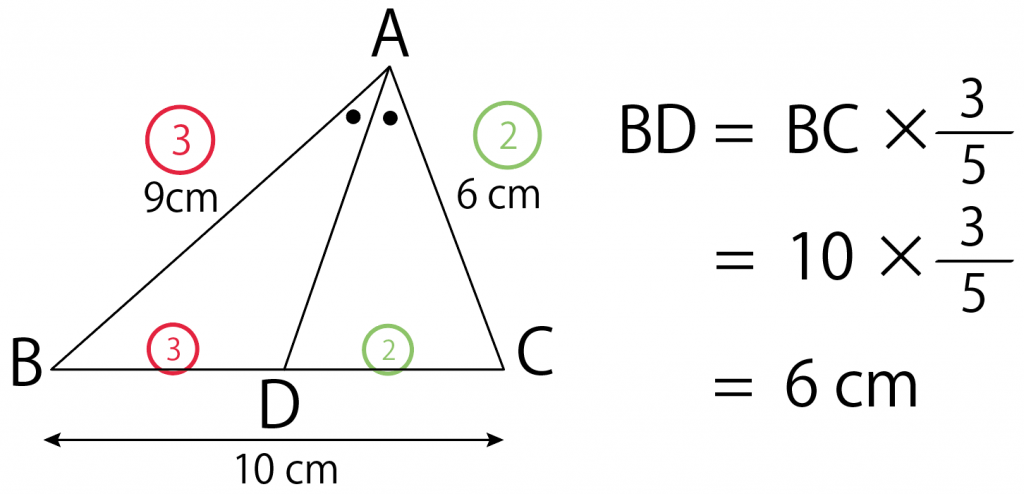
つぎの△ABCにおいて、線分BDの長さを求めなさい。

このタイプの比の問題はつぎの3ステップで解けちゃうんだ。

三角形の2つの辺の比を求める
底辺の比を求める
比で計算する

Step1. 三角形の2つの辺の比を求める

まずは、三角形の2つの辺の比を求めてみよう。

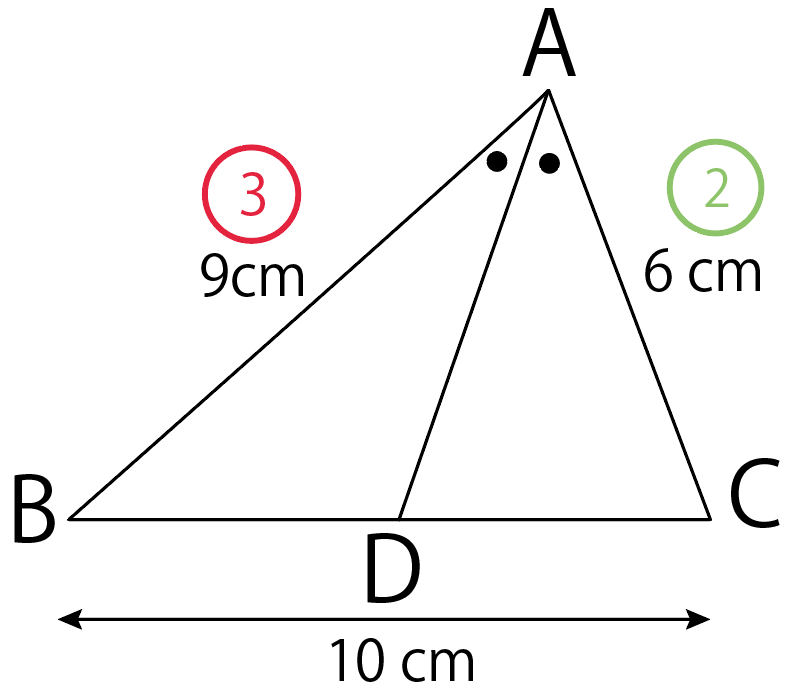
練習問題でいうと、

の2辺だね。

こいつの辺の比を求めてみると、

AB : AC = 9 : 6 = 3 :2

になる！

これが第一ステップ。

Step2. 底辺の比を求める

いよいよ三角形の角の二等分線の定理の出番だ。

さっき求めた「三角形の2辺の比」と「二等分線と底辺の交点でできた線分の比」が等しいってことがいえるからね。

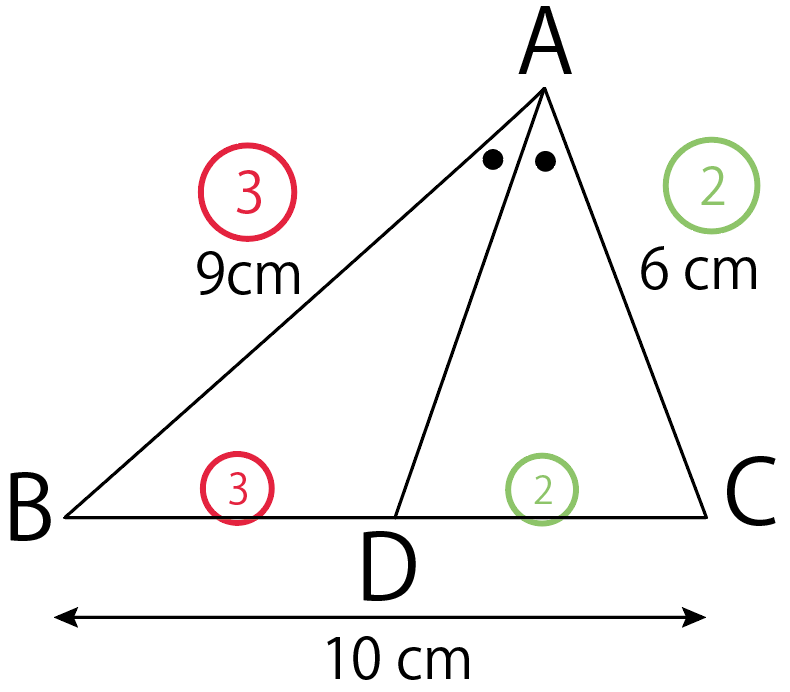
練習問題でいうと、

AB : AC = BD : DC

が言えるわけ。

ステップ1で、AB : AC = 3 : 2がわかったから、

BD : DC = 3 : 2

ってことがわかるね。

これが第二ステップ！

Step3. 比で計算する

求めた辺の比を使って、辺の長さを計算しよう。

練習問題でいうと、

BD : DC = 3 : 2

っていう比をつかって、BDの長さを求めればいいね。

底辺BCの長さは10cmだったから、

BD = 10 × 5分の3 = 6 cm

になるんだ。

三角形の角の二等分線の性質の問題にチャレンジ！！

角の二等分線の性質の問題はどうだったかな？？

三角形の2つの辺の比を求める
底辺の比を求める
比で計算する

の3ステップでだいたい解けそうだったね。

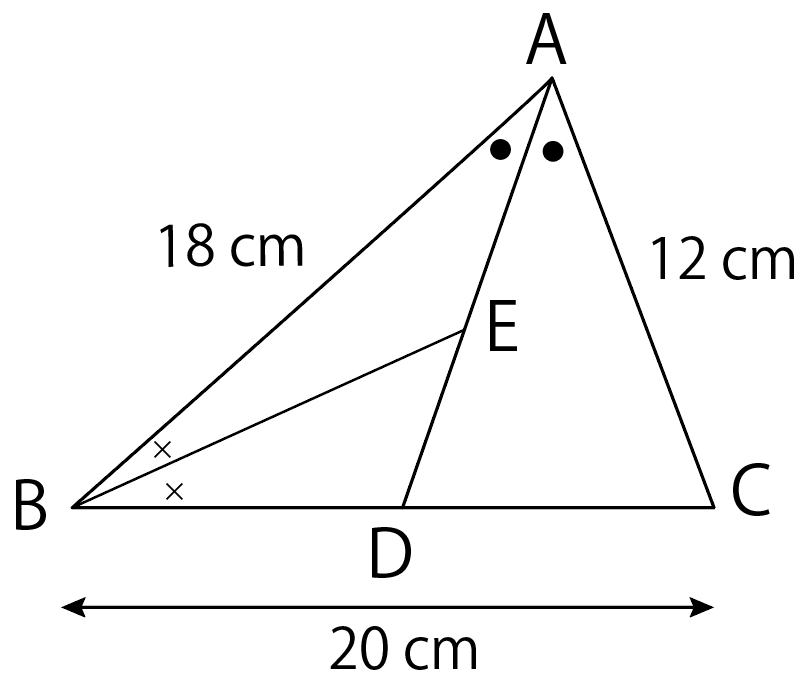
最後につぎの応用問題を解いてみよう！

つぎの△ABCにおいて、AE : EDを求めなさい。

そんじゃねー

Ken