【数学証明】仮定・結論とはいったいなにもの??
証明の「仮定」と「結論」ってなにもの??
こんにちは!この記事をかいているKenだよ。ビタミンCがほしいね。
数学の証明を勉強していると、
仮定
とか、
結論
っていうムズい用語言葉がでてくるね。
日常生活で使わないから、
わけわからないよね??

そこで今日は、
「仮定」と「結論」という用語をわかりやすく解説していくよ。
よかったら参考にしてみてね。
〜もくじ〜
- 仮定とは??
- 結論とは??
数学の「仮定」ってどういうこと??
まずは仮定からみていこう。
意味を辞書(デジタル大辞泉)でしらべてみると、
1) 未定のこと、不確かなことを仮にこうと定めること。また、仮に定めた事柄。「今ここにコップがあると仮定してみよう」「仮定の上に立って物を言う」
2 ) 論理学などで、ある命題を導き出す推論の出発点におかれる前提条件。
ってかいてある。
数学の証明では2つめの意味がそれにあたるんだけど、正直よくわからないよね?。
あまりにも中学生にはむずかしすぎる・・・たぶん、大人にもむずい・・・
そこで、もう少し簡単にいってやると、
ある問題においてのみ、仮に正しいとされたこと
といえる。
えっ。これでもよくわらかないって!?
そうだな、たとえばつぎの問題があったとしよう。
例題
AB = AC である△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
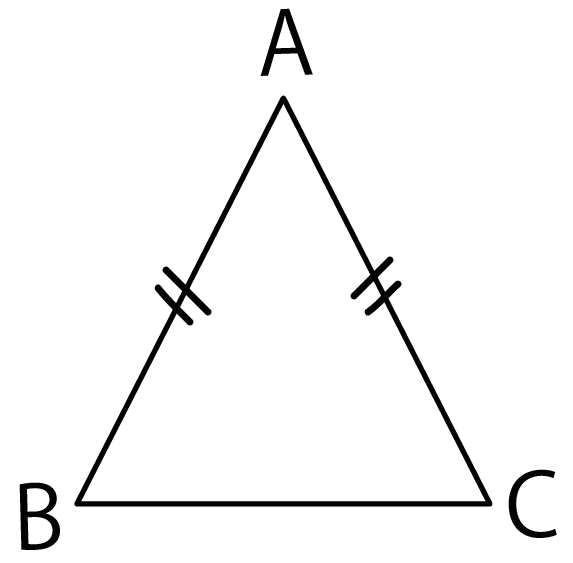
この問題のいっちゃんはじめに、
AB = AC である△ABCがあるとします。
ってかいてあるね。
じつはこの「AB = AC」はこの問題限定でいえること。
世界中に存在する△ABCのすべてが「AB = AC 」ってわけじゃあない。
AB = BCの△ABCもいるかもしれないし、
はたまた、
辺がぜんぜん等しくない△ABCもいるかもしれないね。
だから、
「AB = AC」は例題限定で正しいとしていることだから、
こいつは「仮定」なんだ。
どう?ちょっとスッキリしたかな?
じゃあ結論っていったいなにもの??
結論は、
仮定をつかって正しいといえること
だよ。仮定がなければ結論をみちびけない。
たとえ、どんなに天才だとしてもね。
さっきの例題をみていみよう。
例題
AB = AC である△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
この問題の仮定は、
AB = AC
だったね。
この仮定があるから、結論である「△ABCは二等辺三角形である」っていう結論がみちびけるんだ。
なぜなら、2つの辺が等しい三角形は二等辺三角形だからね。
もし、仮定がない問題だったら↓↓
例題
△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
これはね、無理。無理だよ。
この問題には仮定がどこにもない。
△ABCが二等辺三角形であるって結論を導けるわけがないんだ。
「仮定」をつかってみちびける事実を「結論」という
ことをおぼえておこう。
まとめ:仮定と結論は証明問題には必須!
「仮定」と「結論」は証明問題には必要不可欠なものさ。
なぜなら、証明とは、
与えられた仮定をつかって結論を論理的にみちびくこと
だからね。
「仮定」や「結論」がない証明問題はたとえるなら、
豚肉がない生姜焼きみたいなもんさ。
テスト前にもう一度復習してみてね。
そんじゃねー
Ken


