なぜ相似比をつかって面積比が計算できるのか??
なんで相似比から面積比がわかるの???
ある日、数学が苦手なかなちゃんは、
面積比の公式をにらんでいました。

だああー!
何で面積比が求まるの?
意味不明!!
おっ!
相似比から面積比もわかるってやつだね。
相似比が面積比に……?
もっとわけわかんない……
よし、じゃあ今回は、
相似比と面積比のつながり
を見つけていこう!
相似比から面積比が求められる2ステップ
相似比から面積比がだせる理由は、
つぎの2ステップをふむとわかりやすいよ。
- 正方形で考える
- 三角形で考える
へー!
2ステップなら楽勝じゃん!
そうそう!
いけるいける!
Step1. 「正方形の面積比を考える」
まずは、
正方形の面積比を考えてみよう。
何で?
面積比の公式をみちびきやすいからかな!
たとえば、
2つの正方形A・Bに注目してみて。
1辺の長さが3cmと5cmの正方形ね。
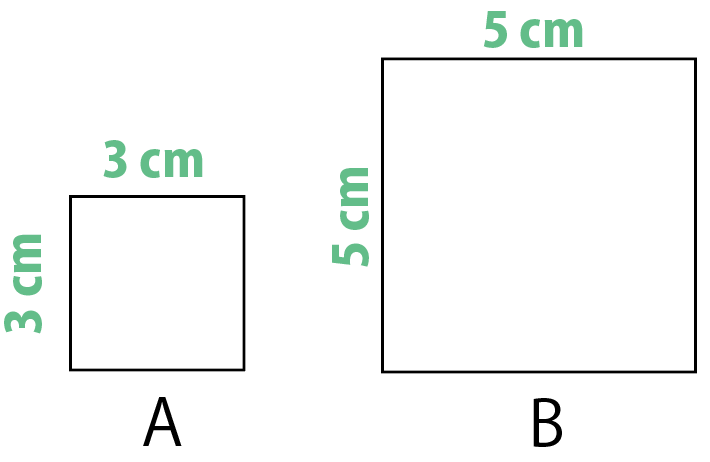
まずは、2つの正方形の面積を求めてみようか。
正方形の面積の公式をつかってね。
正方形の面積の求め方は、
一辺を2乗するだけだよね??
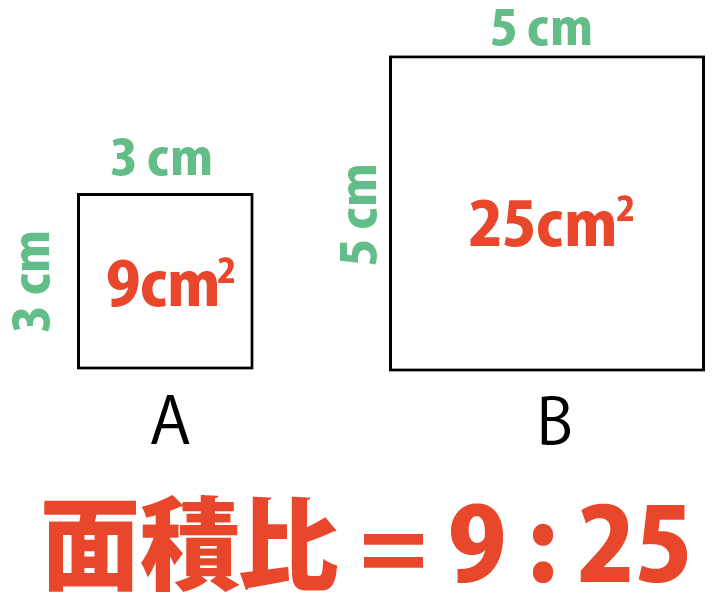
小さい正方形Aの面積は9㎠で、
大きい正方形Bは25㎠かな!
いいね。
次はそこから面積比を求めてみよう!
面積比は、
9:25
だ!
ここで、登場するのが相似比!
2つの正方形の相似比はいくつ??
えっと・・・
相似比は1辺の長さの比をとればいいから、
3:5かな!
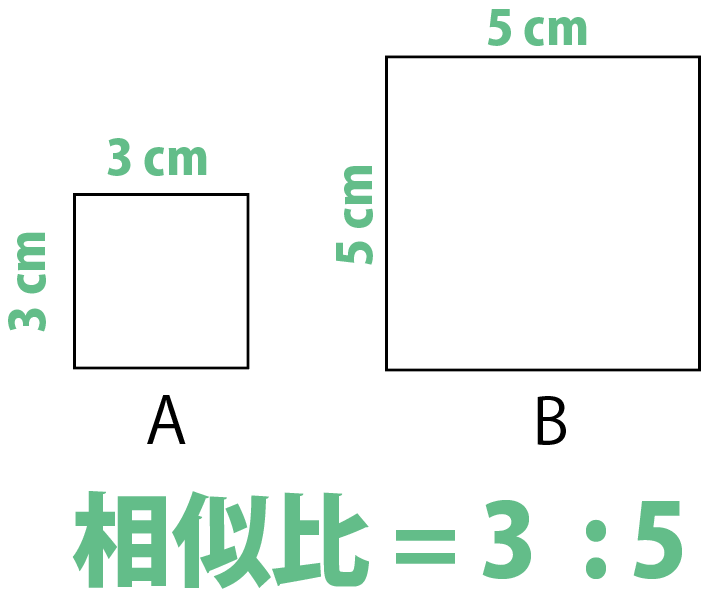
おっ。いいね。
相似比と面積比くらべると・・・??
あっ。
ああああああー
相似比の2乗が面積比になってない??
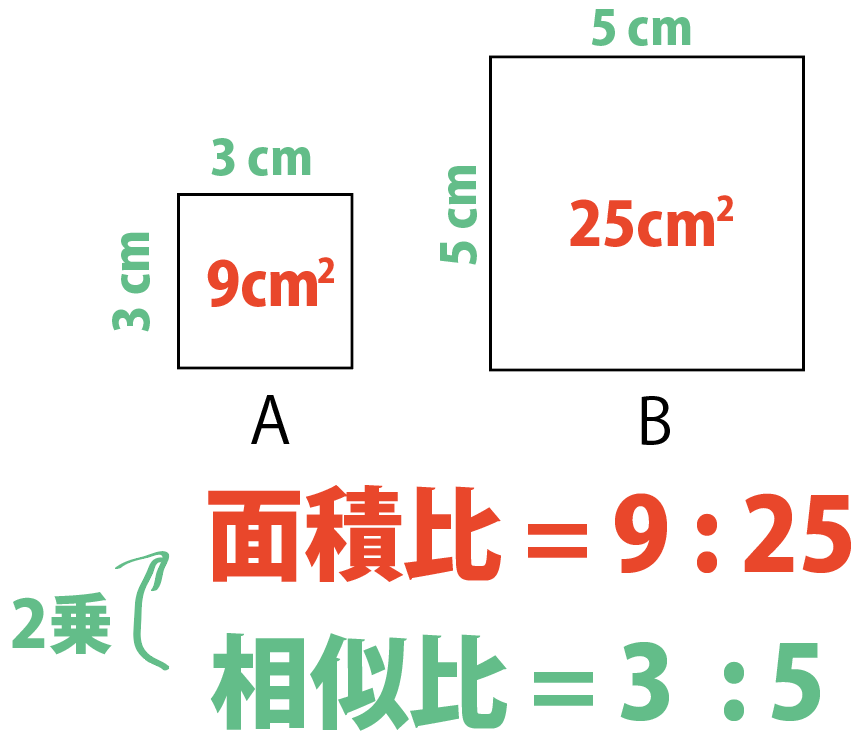
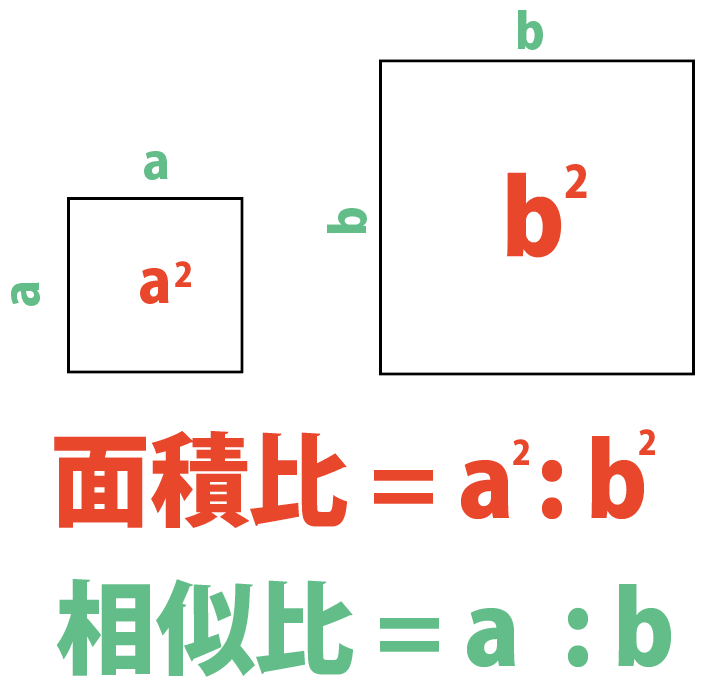
そう!相似比がa:bなら、
面積比はa²:b²になるんだ。
Step2. 「三角形にわけて考える」
形は様々だけど、
どの図形も三角形に切り分けることが出来るんだ。
なるほど!
ってことは、
今度は三角形で考えろってこと?
鋭いね!
次は三角形で考えていくよ。
相似比がa:bの三角形。
それぞれの面積を求めよう。
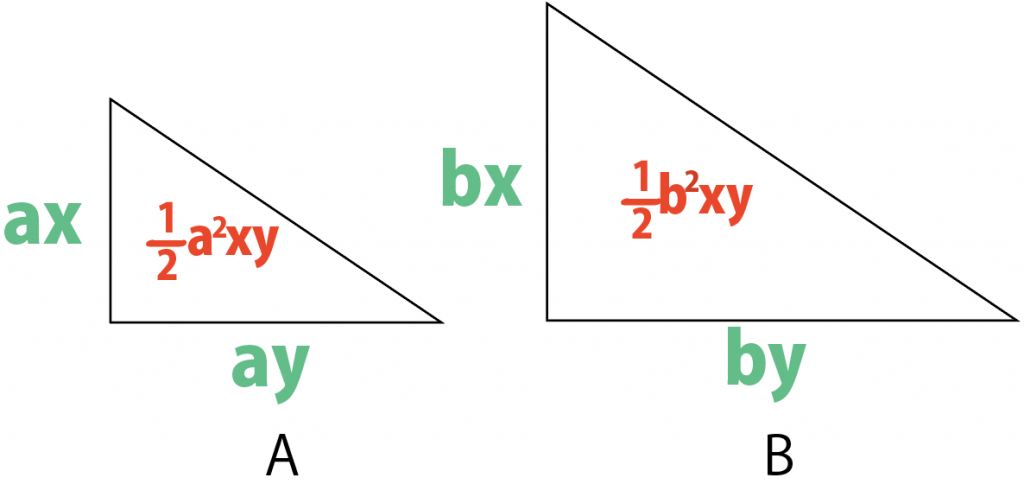
いいね。
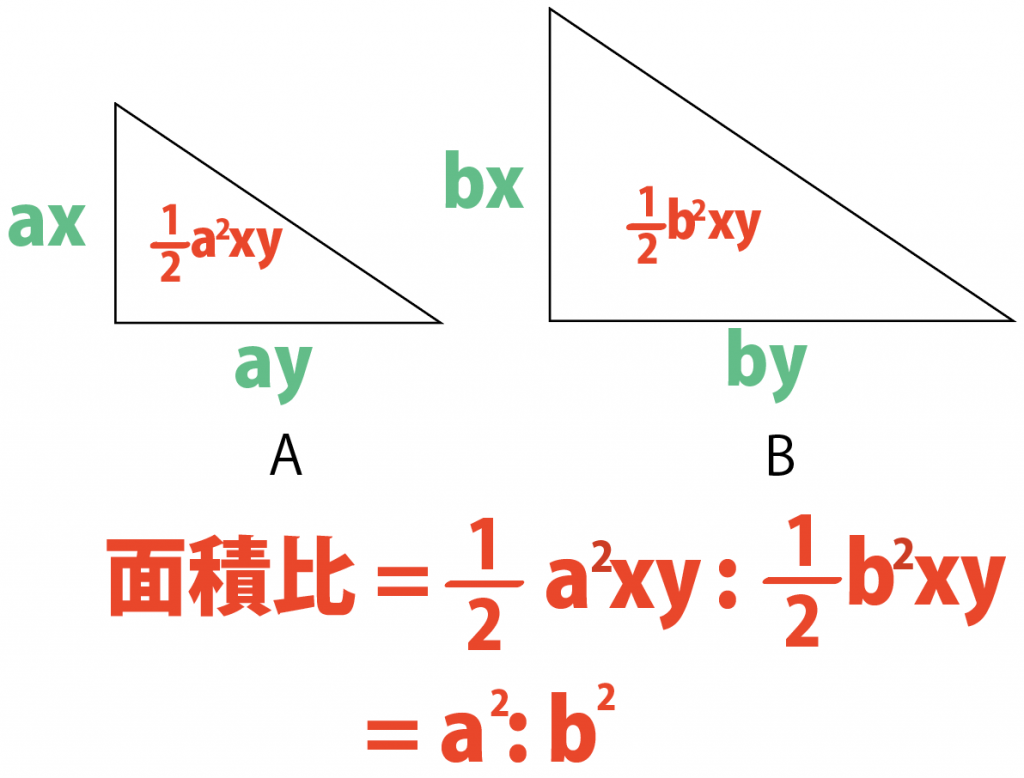
ここで、2つの図形の面積を比べると……?
あっ、
面積比を簡単にすると、
a²:b²になる!
で、他の図形も分けて考えれば三角形と同じだから、
相似比がa:bなら、面積比はa²:b²って関係が当てはまるんだ!
そういうことか!
合点!!
まとめ:相似比を2乗すると面積比になるね!
どう?
何で相似比が分かると、
面積比を求められるのかが分かったかな?
- 正方形で考えてみる
- 三角形で考えてみる
の2ステップでいいんだ。
計算するとそうなるっていうのはわかったけど、
公式は覚えるの嫌だしそもそも覚えられない。
確かに、最初は慣れないし、何度も使うしかないね。
なんか、いい方法ないかな……
正方形を思い出すって手もあるよ。
何がいいかは人それぞれだね。
自分にあった覚え方を見つけてみよう!
ういす!




