【中3数学】2分でわかる!三平方の定理の逆
三平方の定理の逆ってなに??
やあ、Dr.リードだよ。今日は「逆」だよ。逆。
これまで勉強してきた、三平方の定理には、
三平方の定理(ピタゴラスの定理)の逆
っていうのがあるんだ。

逆は中2数学で習ったやつだったね。
忘れてるやつも多いと思うから、逆を復習しつつ、
三平方の定理でも逆が言えるのか??
を見ていこう。
=もくじ=
- 逆の復習
- 三平方の定理の逆って?
- 三平方の定理の逆の証明
- 三平方の定理の逆の問題
中2数学の復習!数学の「逆」ってなに?
まずは数学の「逆」を復習してみよう。
数学の「逆」とはずばり、
ある命題の「仮定」と「結論」を入れ替えたもの
なんだ。
数学の命題とは、「正しいか、正しくないかを考える事柄のこと」だったね。
たとえば、次のような命題があるとするよ。
x =2, y = 3 ならば x+y = 5

仮定と結論をいれかえて、逆を作ってみると、
x+y = 5 ならば x =2, y = 3
になるね。

この命題の逆は正しいかな?
「x+y=5」を満たすxとyの組み合わせって「x=2, y = 3」以外にもありそうだよね?
たとえば、「x = 0、 y = 5」とかね。
だから、この場合は逆にすると命題が成り立たないね。
この例みたいに、
ある命題は正しいけど、逆は正しい場合もあるし、正しくない場合も両方あり得るんだ。
じゃあ三平方の定理の逆とは??
では、三平方の定理の逆はどうだろ。
三平方の定理(ピタゴラスの定理)とはこうだったな。
【三平方の定理(ピタゴラスの定理)】
直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、
a²+b² = c²
が成り立つ。

この三平方の定理(ピタゴラスの定理)で逆をつくってみようか。
三平方の定理の仮定と結論は、
- 仮定:「直角三角形である」
- 結論:「a²+b² = c²」
だ。
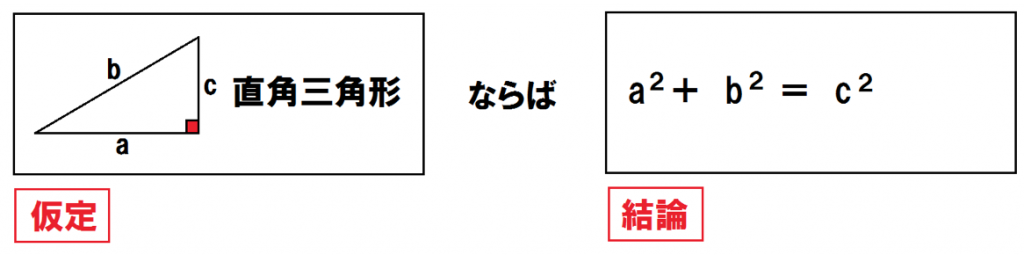
この逆をつくってみると、
- 仮定:「a²+b² = c²」
- 結論:「直角三角形である」
になるね。
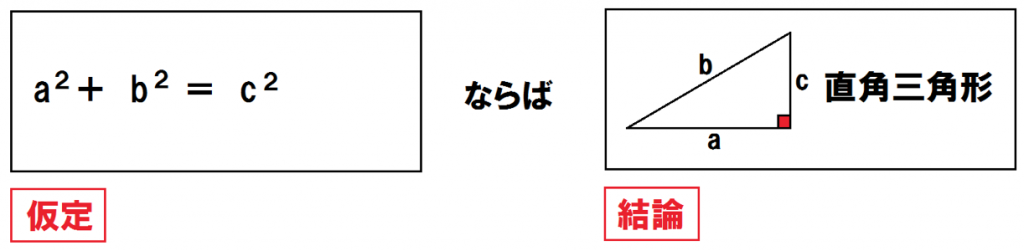
つまり、三平方の定理(ピタゴラスの定理)の逆は、
「a²+b² = c²」ならば「直角三角形である」
だ。
はてさて、これは正しいのかな?
2分でわかる!三平方の定理の逆の証明
三平方の定理の逆の証明してみるか。

わかりきってても、きっちりいくぜぃ。
下の図のような△ABCと△DEFがある。
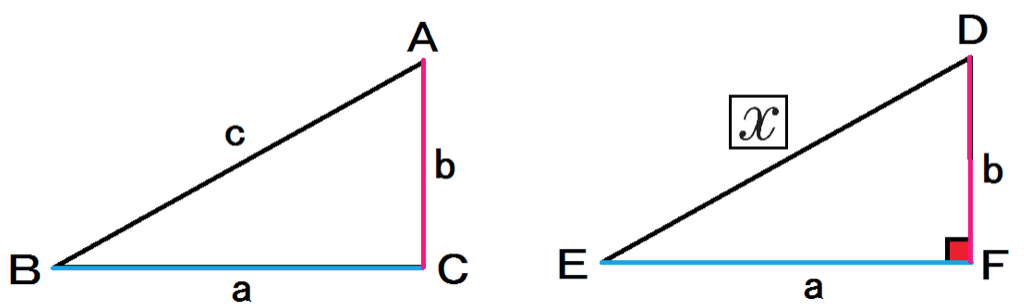
【仮定】
△ABCにおいて a²+b² = c²
△DEFは直角三角形である。
【証明】
△ABC と△DEF について、
仮定より、 a²+b² = c²・・・(1)
△DEFは直角三角形なので 三平方の定理より
a²+b² = x² ・・・(2)
(1)・(2)より、
c² = x²
c も x も正の数なので 、
c = x
△ABCと △DEF の3つの辺がそれぞれ等しいので、
△ABC ≡△DEF
よって ∠BCA =∠EFD=90°
したがって、
△ABC は直角三角形である。
この証明からわかるのは、
三平方の定理の逆も正しい!
ってこと。
中学生ならこの証明で十分かな!

三平方の定理の逆をつかった問題を解いてみよう!
三平方の定理の逆をつかった問題を解いてみよう。
練習問題
次の1辺の三角形があります。直角三角形となるのはどれですか。
(1) 3 cm 4 cm 5 cm
(2) 2 cm √7 cm √10 cm
(3) 15 cm 13 cm 7 cm
(4) 2 cm 2 cm √6 cm
(5) 2√5 cm 2√6 cm 2√7 cm
(6) 2√5 cm 2√5 cm 2√10 cm
2ステップで解けちゃうぜ。
- 斜辺をどれか確認しておく(一番長いのが斜辺)
- 「他の2辺の2乗の和」と「斜辺の2乗」が等しいか確認
(1) 3 cm 4 cm 5 cm
一番長い斜辺は5 cmだから、斜辺の2乗は5² = 25。
他の2辺のに乗の和は、
3² + 4² = 25
になるね。
三平方の定理が成り立つから、直角三角形である!

(2) 2 cm √7 cm √10 cm
斜辺は√10cmだから、斜辺の2乗は、
(√10)² = 10
になる。
他の2辺の2乗の和は、
2² + (√7)² = 11
三平方の定理が成り立たないから、直角三角形ではない。

(3) 15 cm 13 cm 7 cm
一番長い辺の斜辺は15 cm。
斜辺の2乗は 15² = 225。
他の2編の2乗の和は、
7² + 13² = 218
三平方の定理が成り立たないから直角三角形ではない。

(4) 2 cm 2 cm √6 cm
斜辺は√6 cmだから、斜辺の2乗は、
(√6)² = 6
になる。
他の2辺の2乗の和は、
2² + 2² = 8
三平方の定理が成り立たないから直角三角形ではない。

(5) 2√5 cm 2√6 cm 2√7 cm
斜辺は2√7 cmだ。
斜辺の2乗は(√7)² = 7
他の2辺の2乗の和は、
(2√5)² + (2√6)² = 44
三平方の定理が成り立たないから直角三角形ではない。

(6) 2√5 cm 2√5 cm 2√10 cm
斜辺は2√10 cmだから、斜辺の2乗は (2√10)² = 40になる。
他の2辺の2乗の和は、
(2√5)² + (2√5)² = 40
三平方の定理が成り立つから、直角三角形。

まとめ:三平方の定理も逆も使いこなせ!
三平方の定理の逆はどうだったかな?
散々「ピタゴラスった!」から慣れたようだね。
つぎは立体で三平方の定理を使えるようになってみよう!
それじゃあな!
Dr.リード


