辺の比が3:4:5の直角三角形の問題の解き方って？？
こんにちは！この記事をかいてるKenです。良薬は苦しだね。
直角三角形の辺の比の問題でよく出てくるパターンの1つに、
3: 4: 5の直角三角形
っていうのがあるんだ。
これは文字通り、
3つの辺の比が3:4:5になってる直角三角形のことね。
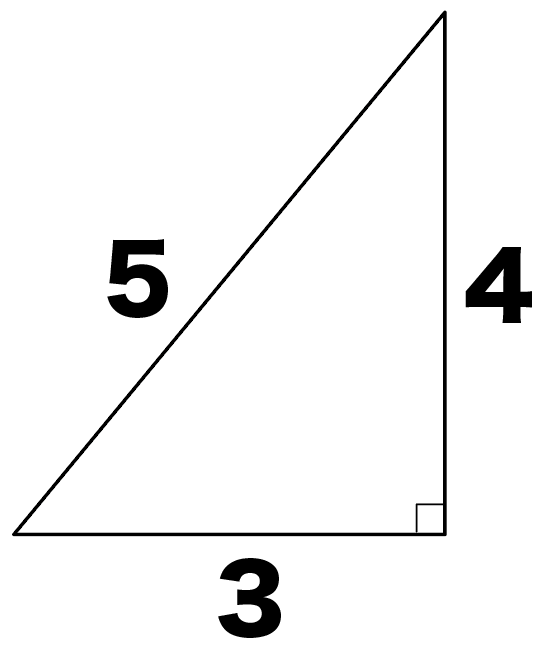
たとえば、辺の長さが、
- 30000 cm
- 40000 cm
- 50000 cm
になってる直角三角形。
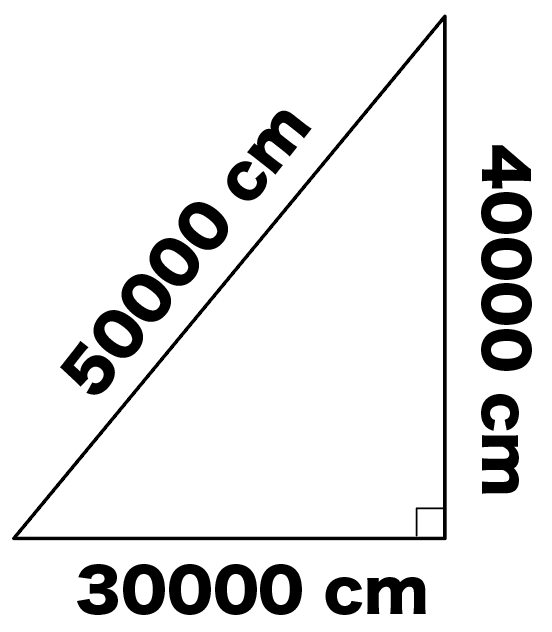
辺の長さの比を取ってみると、
30000 : 40000 : 50000
= 3 : 4 :5
になってるでしょ？？
今日はこんな感じで、
3:4:5の直角三角形の辺の長さを求める問題
の解き方紹介していくよ。
よかったら参考にしてみてね。
辺の比が3:4:5になってる直角三角形の3つの問題
3:4:5の直角三角形の辺の比の問題は3種類あるよ。
- 斜辺以外の辺の比が3:4のとき
- 斜辺とその他の辺の比が5:4のとき
- 斜辺とその他の辺の比が5:3のとき
問題1. 「斜辺以外の辺の比が3:4のとき」
一つ目のパターンは、
斜辺以外の辺の比が3:4の問題だね。
直角三角形の辺の比を使えば、三平方の定理より早く解けちゃうんだ。
たとえば、つぎのような練習問題ね。
練習問題
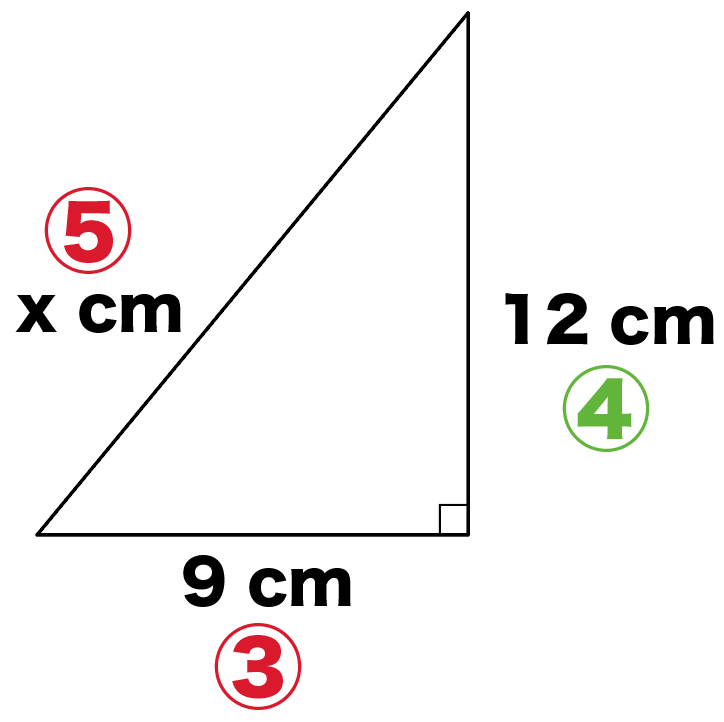
直角三角形の辺の長さxを求めなさい。
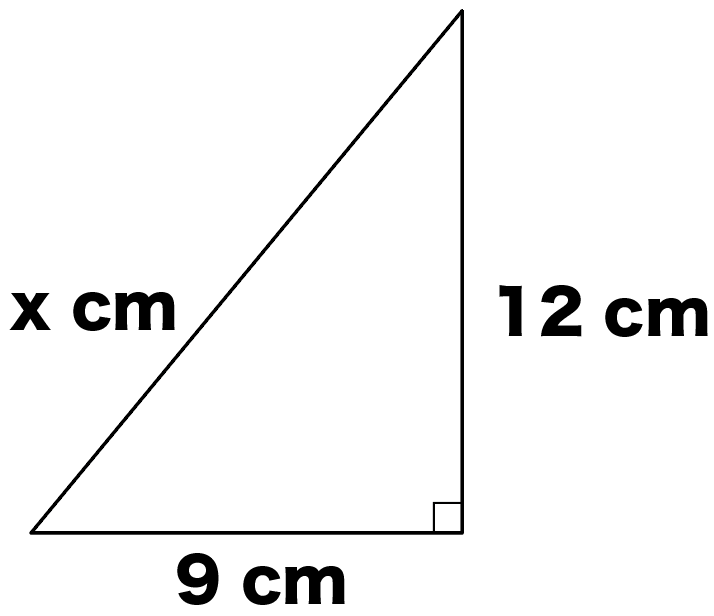
直角三角形の斜辺以外の辺の比をみてみると、
9 : 12
= 3 : 4
になってるよね？？
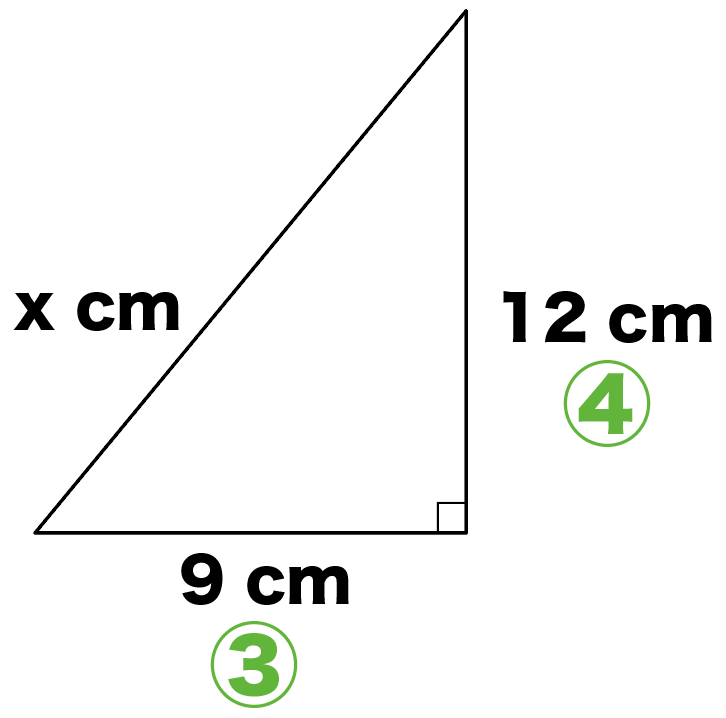
ってことは、これは紛れもなく3:4:5の直角三角形。
この手の問題では、
「1番小さい辺の長さ」に3分の5をかければ斜辺の長さを計算できるんだ。
なぜなら、
（斜辺の長さ）：（1番小さい辺の長さ）= 5 : 3
になってるはずだからね。
ってことで、1番小さい辺の「9 cm」に3分の5をかけてやると、
9× 5/3
= 15 cm
に斜辺はなるね。
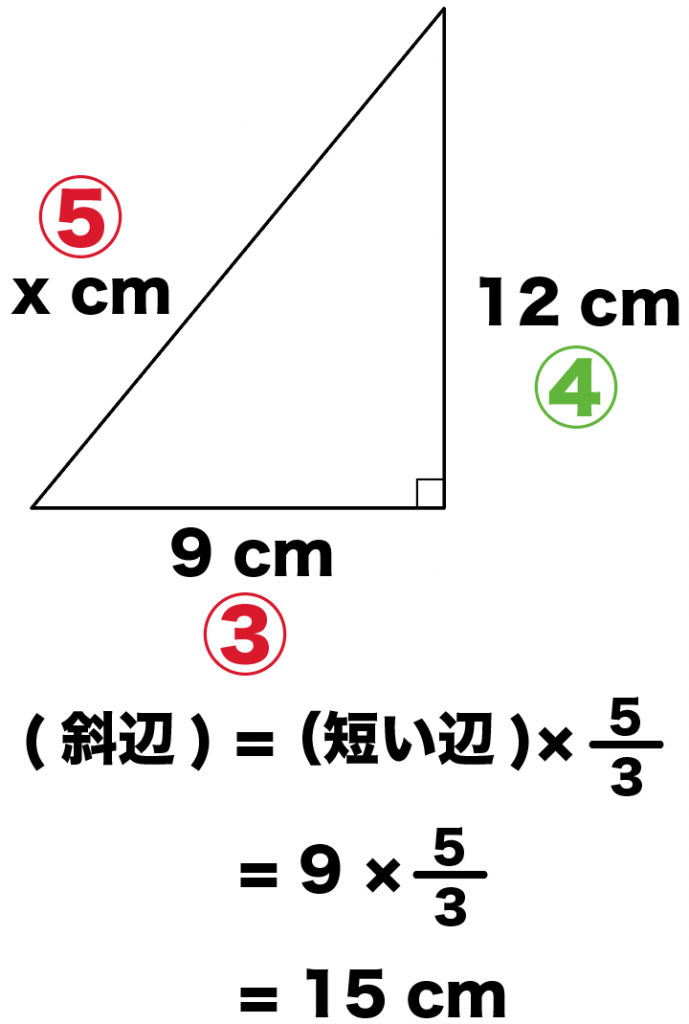
三平方の定理を使うより早くて簡単だ。
問題2. 「斜辺とその他の辺の比が5:4のとき」
つぎは「斜辺」と「その他の辺」の比が5:4の問題ね。
練習問題
つぎの直角三角形の辺の長さxを求めなさい。
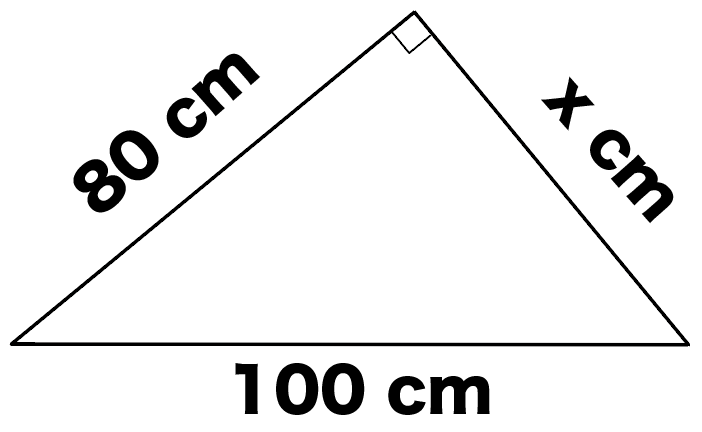
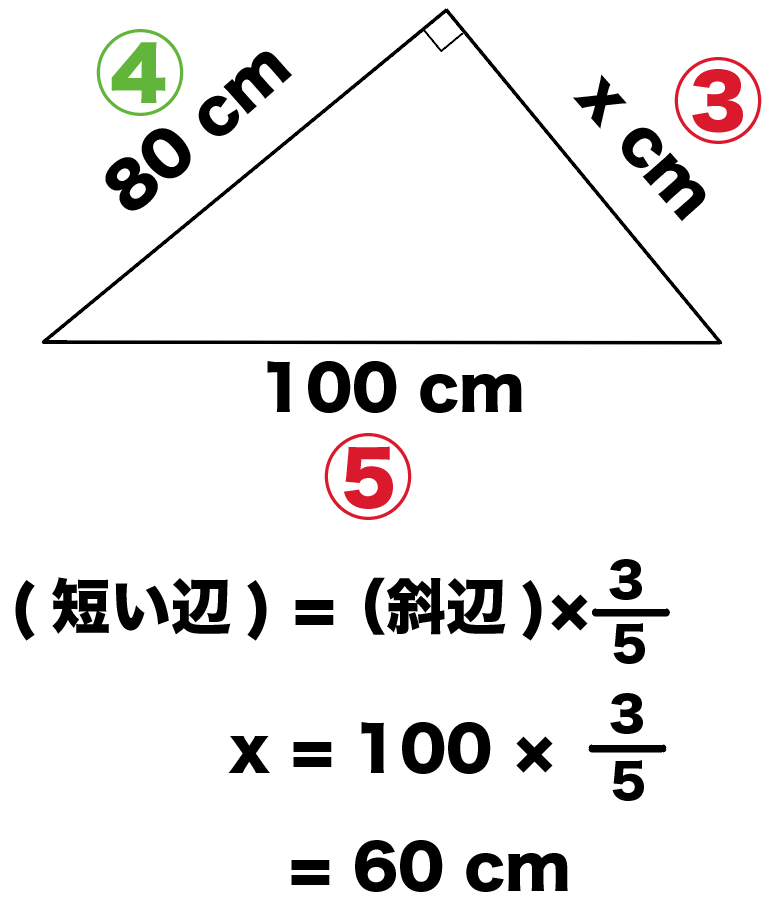
この問題では、「斜辺」と「もう1辺の長さ」の辺の比が、
100 : 80
= 5 : 4
になってるよね？？
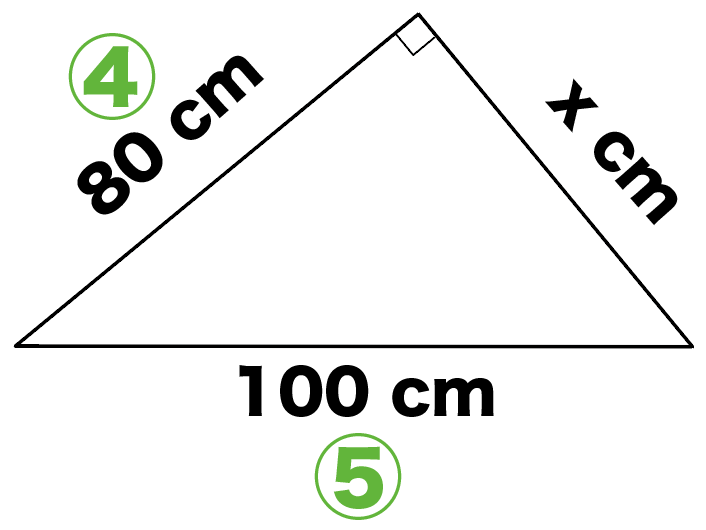
ってことは、直角三角形の辺の比は3:4:5になるはずだから、
「斜辺の長さ」に5分の3をかければ残りの辺の長さを計算できちゃうね。
ってことで、残りの辺の長さxは、
x = 100×5分の3
= 60 cm
になるね。
問題3. 「斜辺とその他の辺の比が5:3のとき」
最後は、「斜辺」と「その他の辺」の比が5:3になってる問題ね。
たとえば、つぎのようなやつ。
練習問題
つぎの直角三角形の辺の長さxを求めなさい。
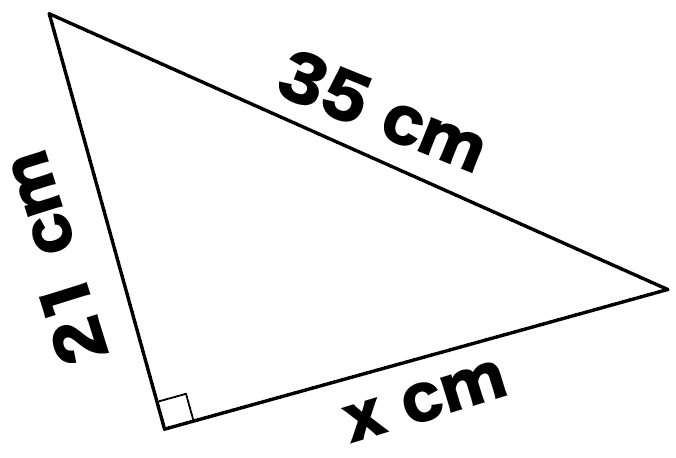
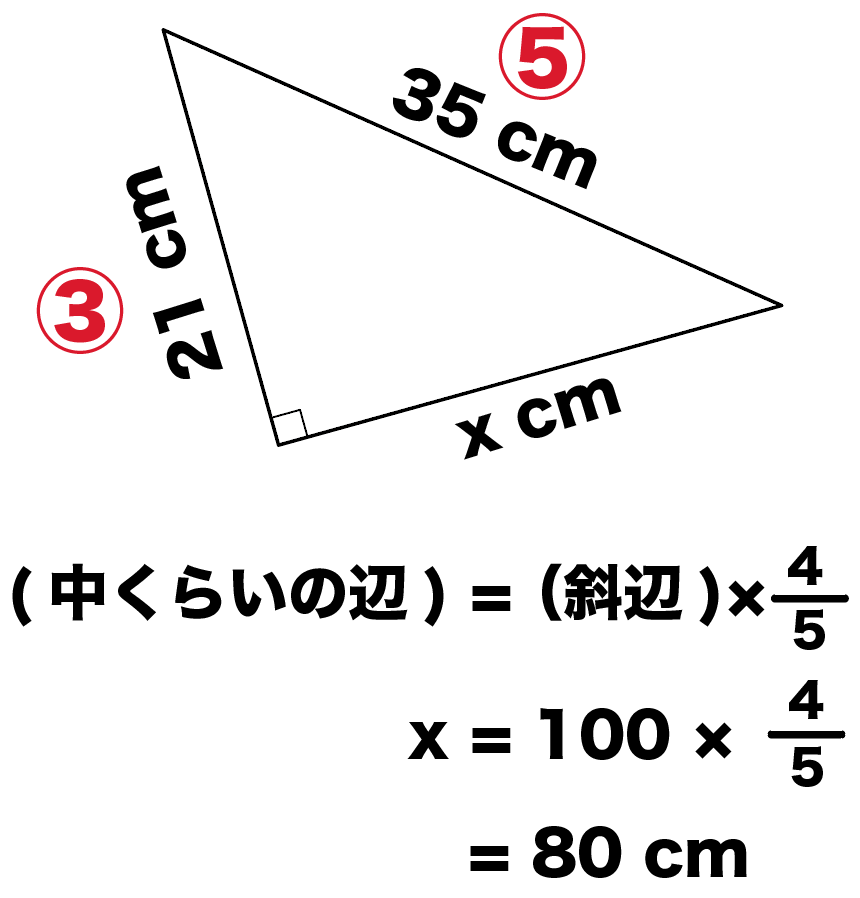
直角三角形の「斜辺」と「その他の一辺の長さ」の比を出してみると、
35 : 21
= 5 : 3
になってるよね？
ってことはこの直角三角形も3:4:5のタイプ。
斜辺と残りの辺の長さの比は、
5: 4
になってるはずだから、斜辺に5分の4をかければ辺の長さが出てくる。
実際に計算してみると、
x = 35×4/5
= 28 cm
になるね。
まとめ：辺の比が3:4:5の直角三角形の問題は分数の掛け算だけ！
辺の比が3:4:5の直角三角形の問題はどうだったかな？？
全部で、
- 斜辺以外の辺の比が3:4のとき
- 斜辺とその他の辺の比が5:4のとき
- 斜辺とその他の辺の比が5:3のとき
の3パターンあったけど、やってることは全部一緒。
3:4:5の辺の比を使って分数の掛け算すればいいのさ。
コツは、
辺の比が3:4:5になってることをいかに早く見つけるか
だ。
問題をたくさんといて解き方に慣れていこう。
そんじゃねー
Ken
