【中3数学】覚えて損はない!相似な図形の性質2つ
相似な図形の性質ってどんなやつ??
こんにちは、Drリードだよ。
ここまで相似な図形を勉強してきたよね。
相似の記号もおぼえたし、
相似比も求められるようになった。

今日はね、もう一歩踏み込んで、
相似な図形同士がもつ性質を勉強していこう。
相似な図形たちはどんな性質をもっているんだろう??
テストで役立つ!2つの相似な図形の性質
さっそく相似な図形の性質を紹介しよう。
つぎの性質があるんだ。
- 対応する線分の長さの比はすべて等しい
- 対応する角の大きさはそれぞれ等しい
つぎの△ABCを想像してみて。
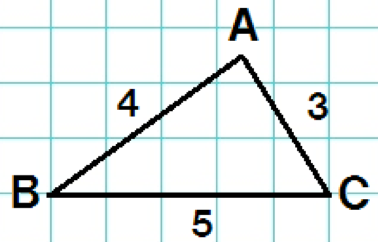
こいつを2倍に拡大してみよう。
スマホやタブレットの画面で、
「ピンチ」して2本指で画面を拡大したことあるよね?

その調子で、△ABCも拡大してみると、
ほれ!
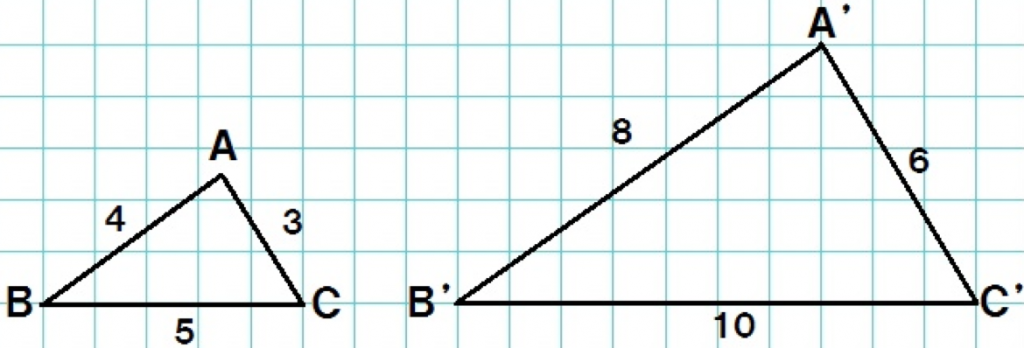
△ABCの2倍の△A’B’C’のできあがりさ。
この2つの三角形をつかって、
相似な図形の性質を確認していこうか。
性質1. 「対応する線分の長さの比はそれぞれ等しい」
相似な図形の性質の1つめは、
対応する線分の長さの比が等しい
ってやつだ。
つまり、ぜんぶの辺の比が同じになってるって性質ね。
それじゃあ、
「△ABC」と「2倍に拡大した△A’B’C’」の、
対応する辺を確認していこう。
対応する辺はそれぞれ、
- ABとA’B’
- BCとB’C’
- ACとA’C’
だね。
色でわけてみたよ↓↓
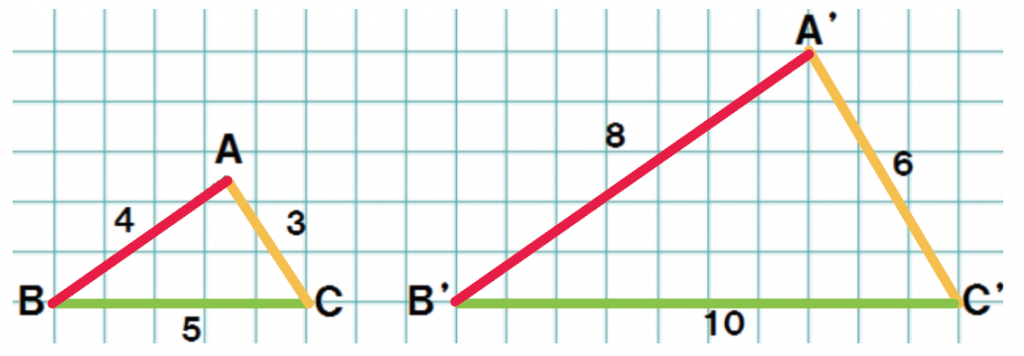
対応する辺の長さについて調べみると、
- A’B’ = 2AB
- B’C’ = 2BC
- C’A’ = 2CA
うんうん、
△A’B’C’ の辺の長さは△ABCの辺の2倍になってるね。
辺の長さの比を書くと、
- A’B’ : AB = 2 : 1
- B’C’ : BC = 2 : 1
- C’A’ : CA = 2 : 1
になってるね。
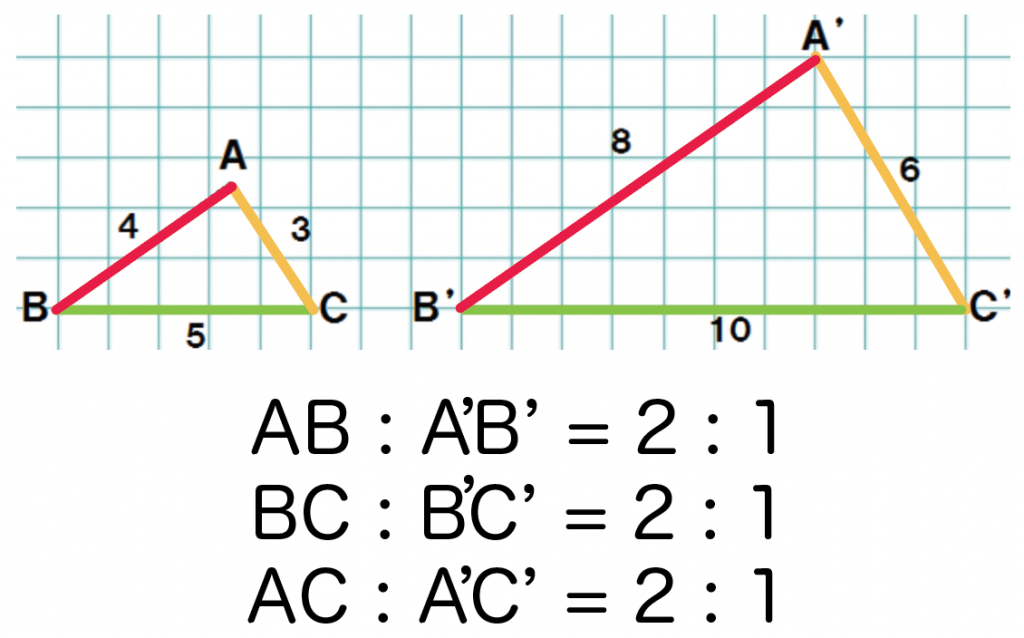
あ!
ぜーんぶの比が2: 1になっとるやん!
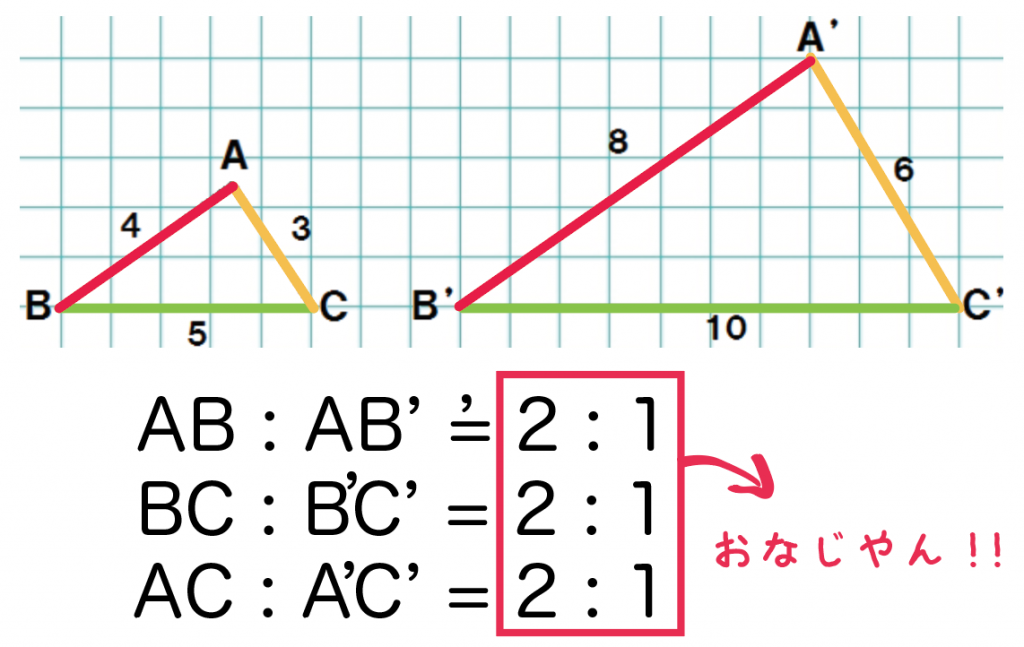
ってことは、
対応する辺(線分)の長さの比はすべて等しい
っていえるね。
これが相似な図形の1つめの性質だ。
性質2. 「対応する角の大きさはそれぞれ等しい」
2つめの相似な図形の性質は、
対応する角の大きさが等しい
ってやつね。
簡単にいってやると、
相似な図形の角度はぜんぶ等しいよ!
ってこと。
ためしに、△ABCと△A’B’C’をみてみようか。
実際に分度器で角度をはかってみると、
うわ!
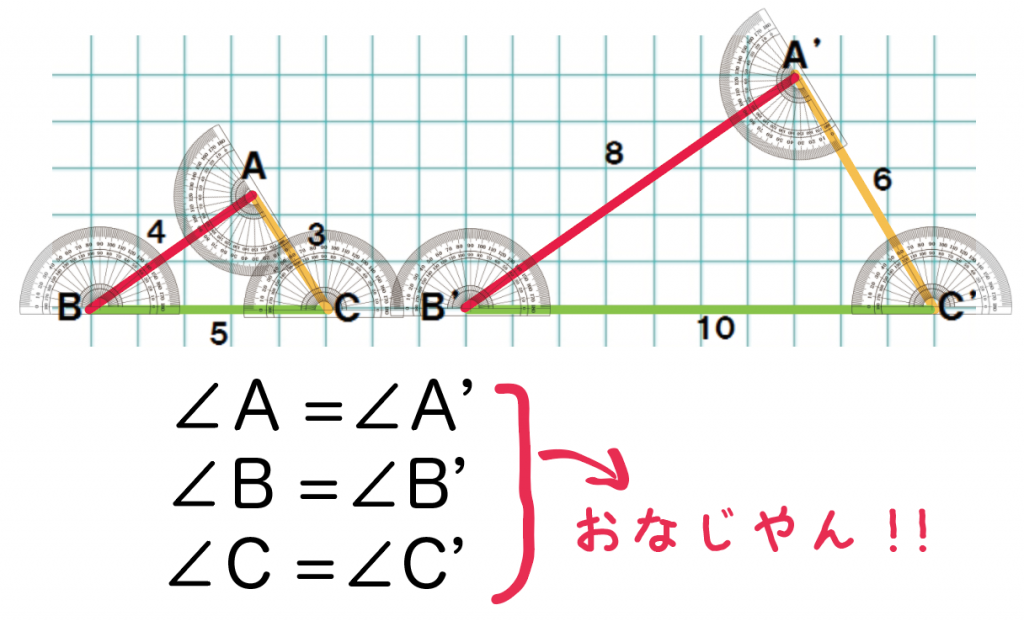
いっしょじゃん!
対応する角たちが等しくなってる!!
- 角A = 角A’
- 角B = 角B’
- 角C = 角C’
えっ。うさんくさいって??
そういうときは、2つの図形をかさねてみて。
ほら?
きれいに重なるでしょ?
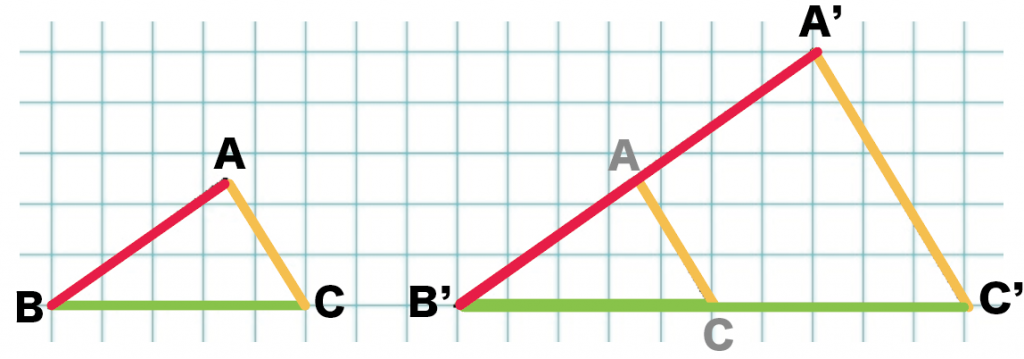
こんなかんじで、
2つの相似な図形の角度は、
ぜーんぶ等しいっていう性質があるんだ!
まとめ:相似な図形の性質は2つだけ!
相似な図形の性質を忘れないように復習しておこう。
相似な図形の性質は、
- 対応する線分の長さの比はすべて等しい
- 対応する角の大きさはそれぞれ等しい
の2つだったね??

この2つの性質は基本中の基本。
相似な図形を見たときに,
「あ,こことここの角度同じ!」
「相似だから,こことここの比が同じ!」
って気がつくことが大事。
相似の基本的なことだけど、重要だよ。
性質を必ず頭に叩き込んでおこう。
それじゃあ、
Drリード


