中点連結定理をつかった平行四辺形の証明問題！？
どーも、ぺーたーだよ。
中点連結定理をつかった証明問題はたくさん、ある。
なかでもよくでてくるのは、
平行四辺形であることを証明する問題
だ。
たとえば、つぎみたいな証明問題ね。
このとき四角形EFGHが平行四辺形になることを証明しなさい。
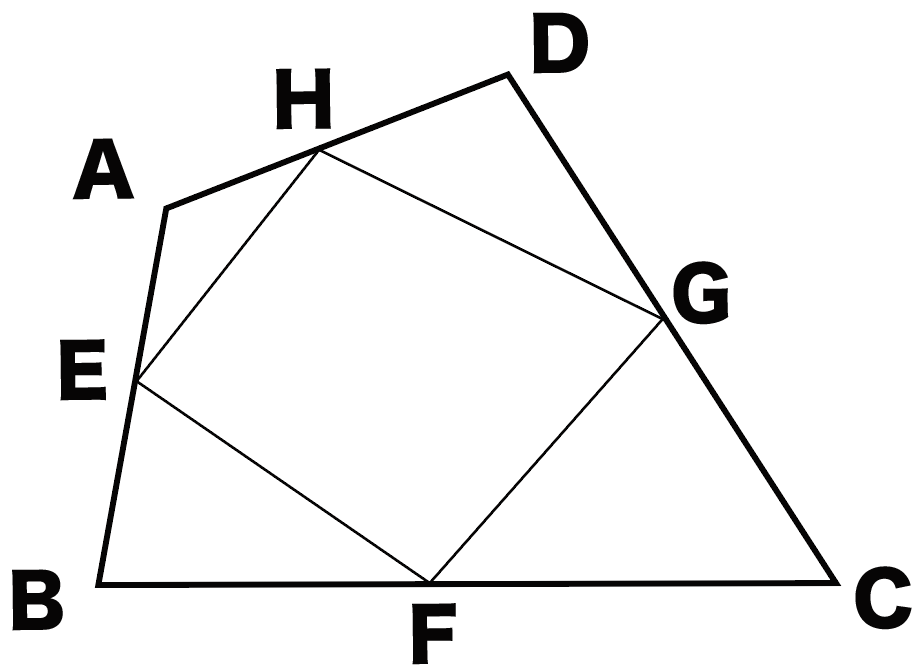
みんなけっこう難しいって
思ってるんじゃないかな？
今回はどうやって、
中点連結定理で平行四辺形を証明するのか
を3ステップで証明していくよ。
中点連結定理で平行四辺形を証明する3つのステップ
さっそく証明問題をといていくよ。
四角形ABCDの4辺AB、BC、CD、DAのそれぞれの中点をE、F、G、Hとする。
このとき四角形EFGHが平行四辺形になることを証明しなさい。
Step1. 対角線をひく
証明を始める前に1つだけやることがあるんだ。
それは、
対角線を1本かいてあげること！
そうするとこうなるね ↓↓
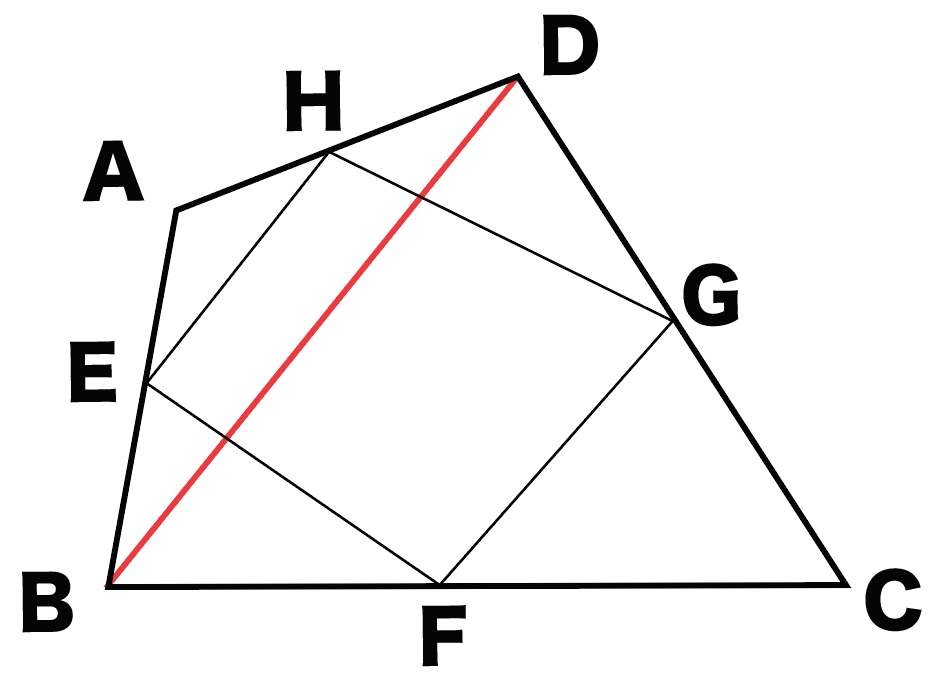
今回は、対角線BDをひいたけど、ACでも同じだからね。
Step2. 中点連結定理をつかう
対角線を引いたら、いくつか三角形が見えてくるよね？
練習問題でいうと、
- △AEH
- △ABD
- △CGF
- △CDB
の4つだね。
平行四辺形を証明するために
2組の三角形に分けてみてみよう。
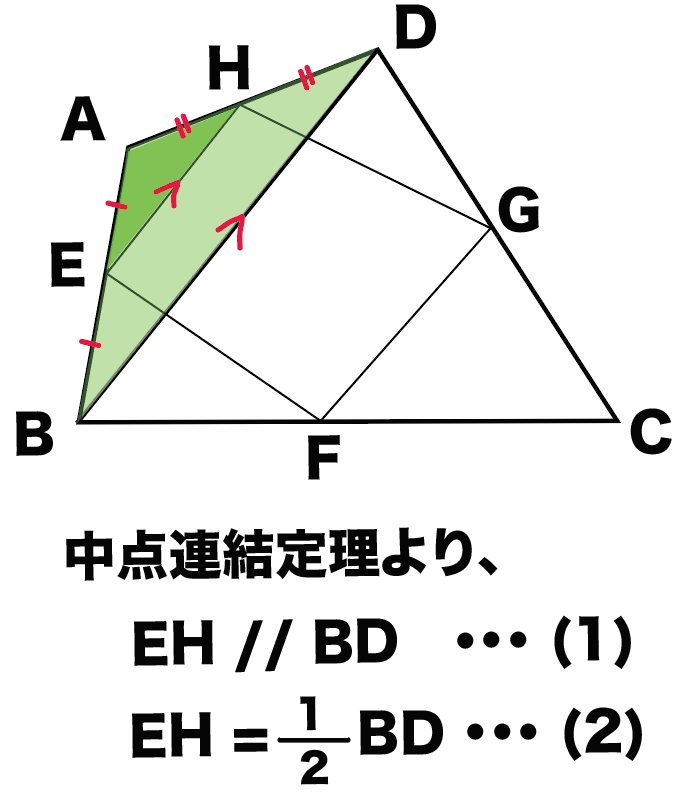
まずは△AEHと△ABDに注目してみて。
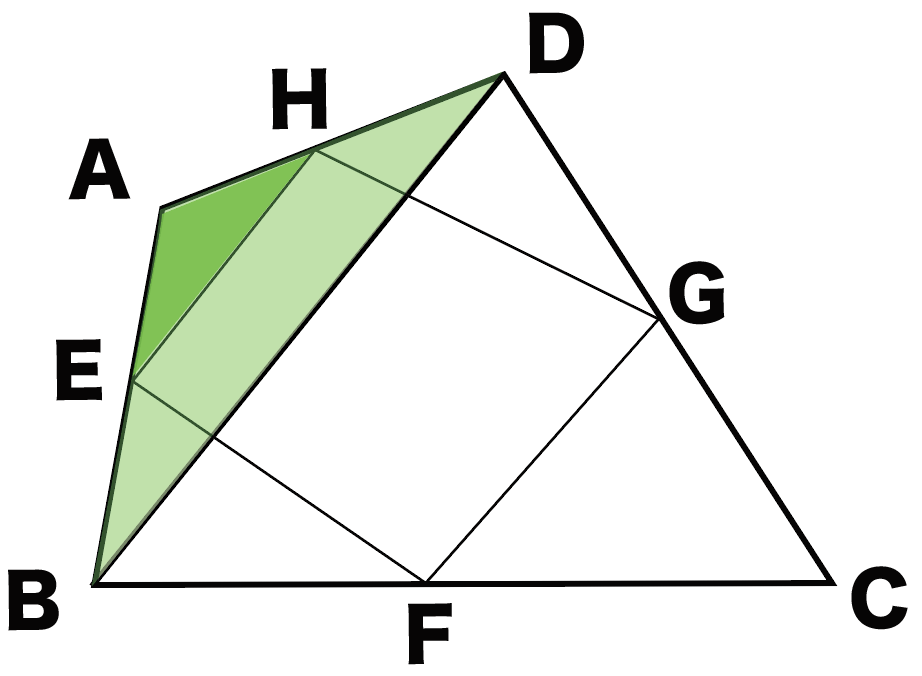
EとHはそれぞれ、
辺ABと辺ADの中点だよね？？
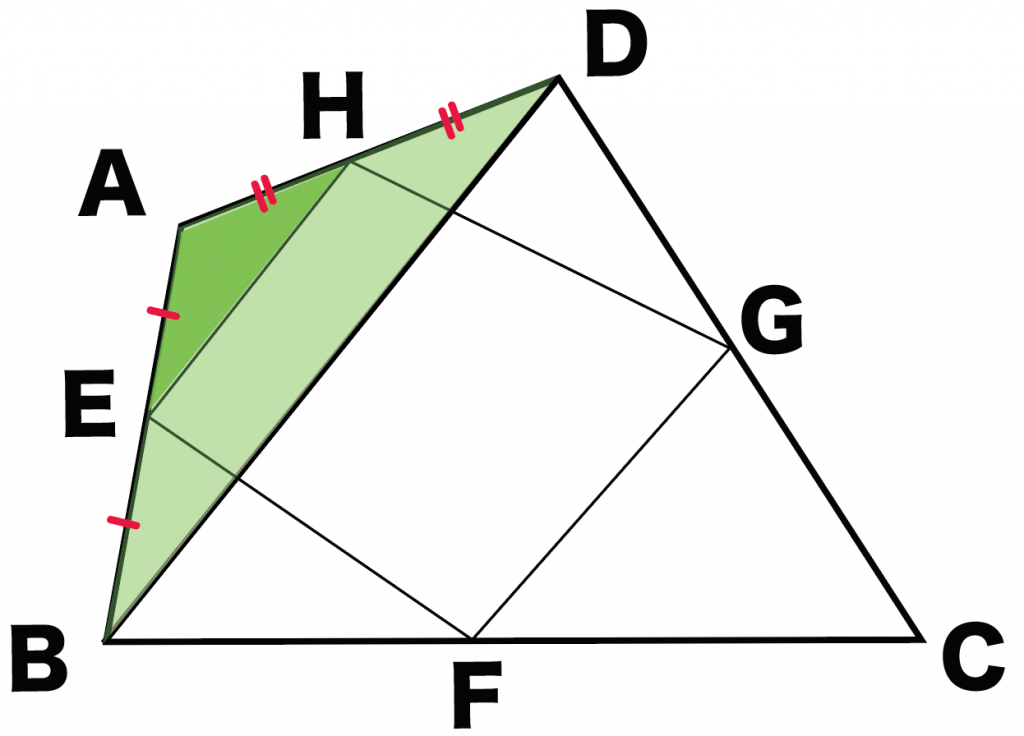
ってことは、中点連結定理をつかうと、
EH // BD・・・(1)
EH = 1/2 BD・・・(2)
がいえるんだ。
おなじことを△CGFと△CDBでもやってみよう。
FとGは、辺BGと辺DCの中点。
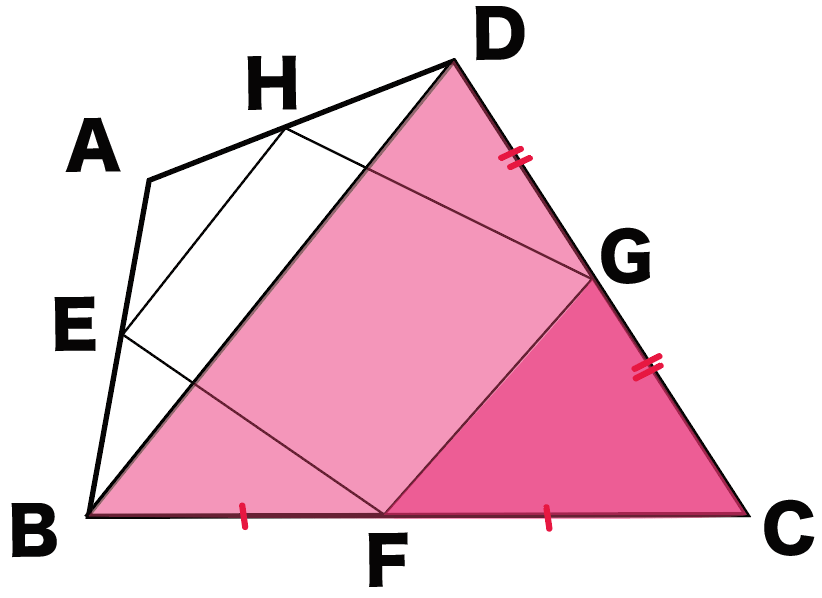
ってことで、中点連結定理がつかえるから、
FG // BD・・・(3)
FG = 1/2 BD・・・(4)
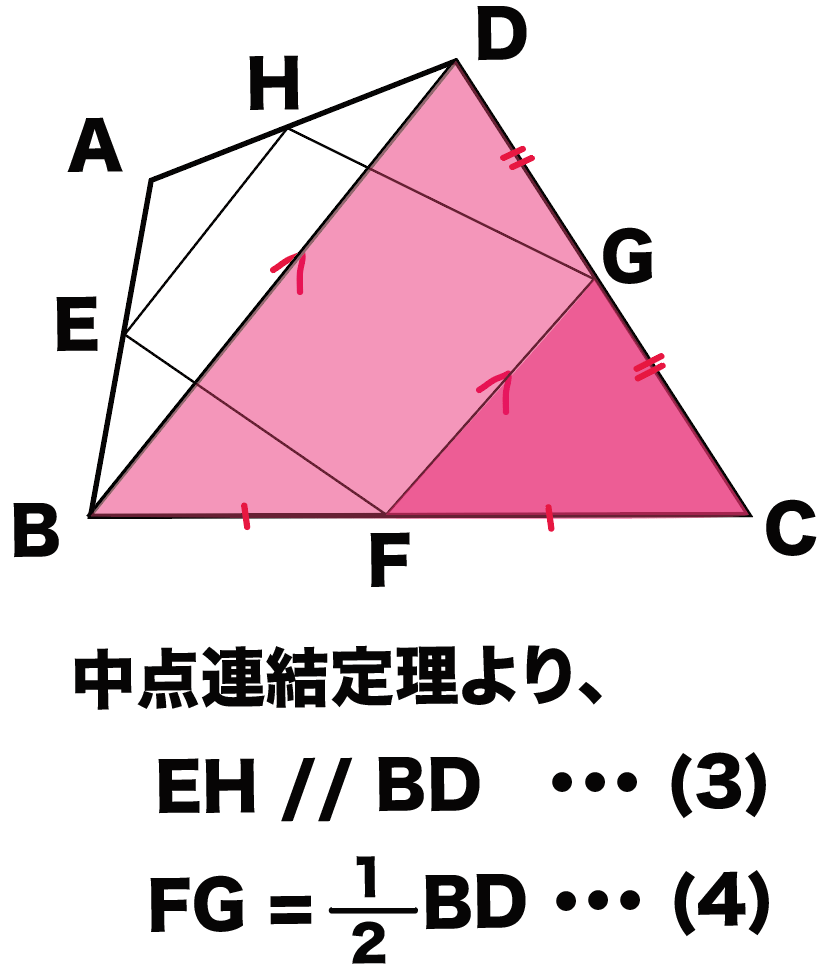
になるね。
Step3. 平行四辺形になる条件をつかう
最後は平行四辺形になる条件をつかうよ。
5つの条件を見なくても言えるかな？（。）
- 2組の向かい合う辺がそれぞれ平行である
- 2組の向かい合う辺がそれぞれ等しい
- 2組の向かい合う角がそれぞれ等しい
- 対角線が中点で交わる
- 1組の対辺が平行で長さが等しい
くわしくは平行四辺形になるための5つの条件をよんでみてね。
ちなみに、中点連結定理を使って平行四辺形を証明する問題は
1組の対辺が平行で長さが等しい
を使うのがほとんど。
今回もこの条件をつかうよ。
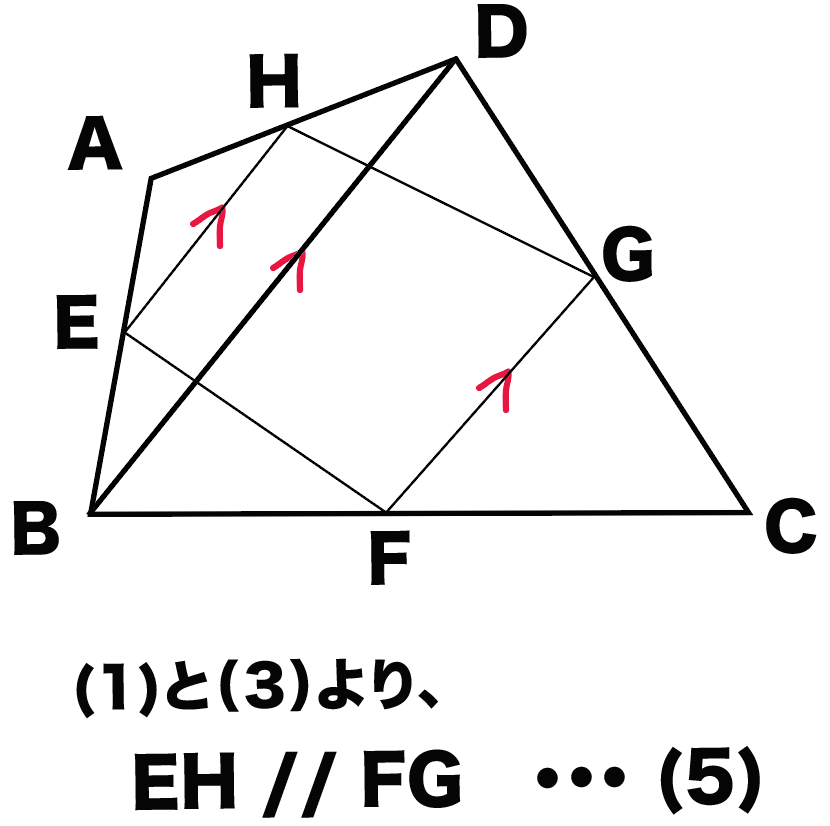
(1)と(3)から、
EH//BD//FGになるね。
つまり、
EH//FG・・・（5）
がいえるわけだね。
また、(2) と (4)から、
EH = FG = 1/2 BD・・・（6）
がいえるね。
EHとFGの両方がBDの半分になってるからさ。
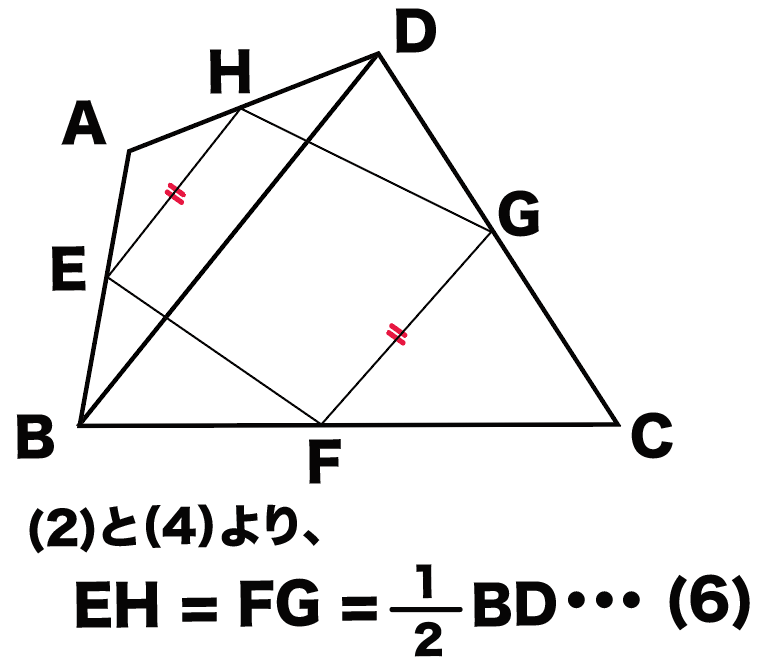
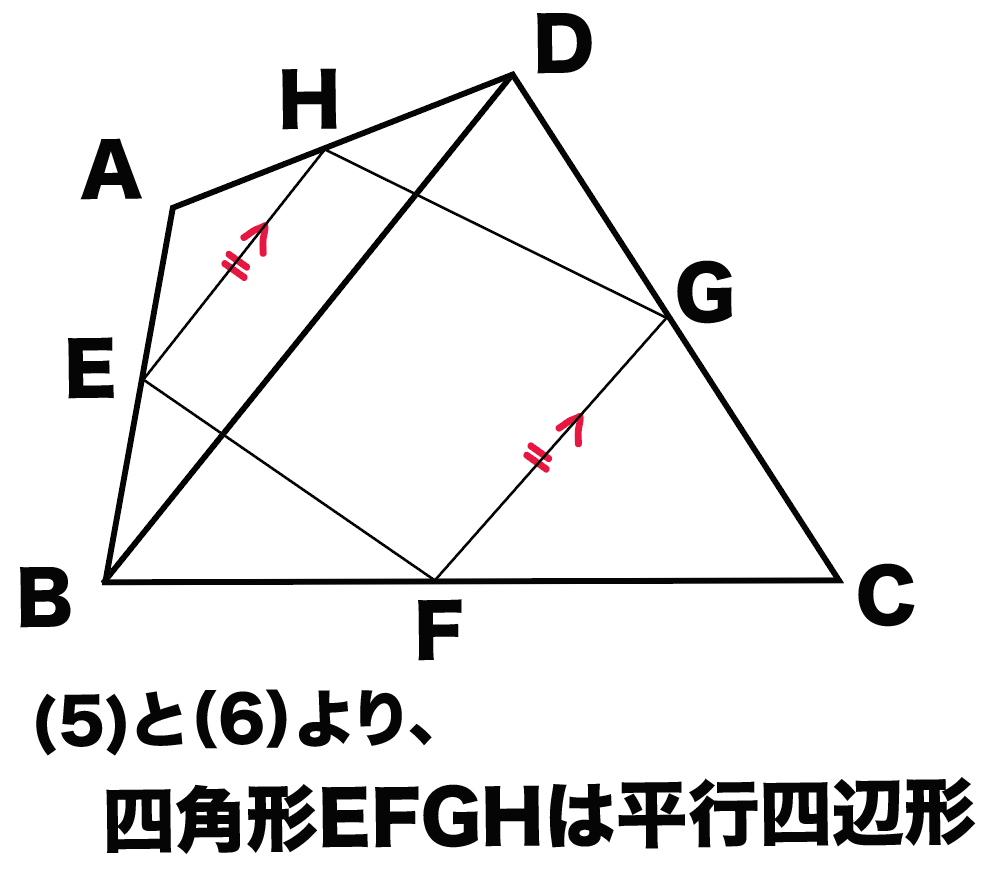
んで、
(5)と(6)より、平行四辺形になる条件の、
1組の対辺が平行で長さが等しい
がつかえるわけだね。
だから、
四角形ABCDは平行四辺形
ってわけ。
おめでとう！
これで証明おしまい！
まとめ：対角線を引いて中点連結定理に持ち込め！
中点連結定理をつかった平行四辺形の証明はどうだった？？
この問題のポイントは、
対角線の補助線がひけるかどうか
だね。
平行四辺形を証明する問題は数をこなすのが一番！
おぼえるまで何回かといてみてね。
じゃあねー
ぺーたー
