【中学数学】相似比の求め方がわかる3ステップ
相似比の求め方をおしえてほしい!!
こんにちは!ぺーたーだよ。
中学3年生で習う相似。
「相似」ってふつうに生活してたら耳にしないよね??
最初はだれもが「ん、相似ってなんだ?」ってなる単元だ。
この単元でいちばん出てくるのは、
相似比を求めるタイプの問題
なんだ。
今日はテストで問題が解けるように、
相似比の求め方を解説していくよ。
よかったら参考にしてみて。
=もくじ=
- そもそも相似・相似比ってなに?
- 相似比の求め方
そもそも相似・相似比ってなんだろう??
相似比の求め方を勉強する前に、まず、
相似とはなにか??
を復習してみようか。
相似な図形とはずばり、
1つの図形の形を変えずに大きくしたり小さくした図形のことだよ。
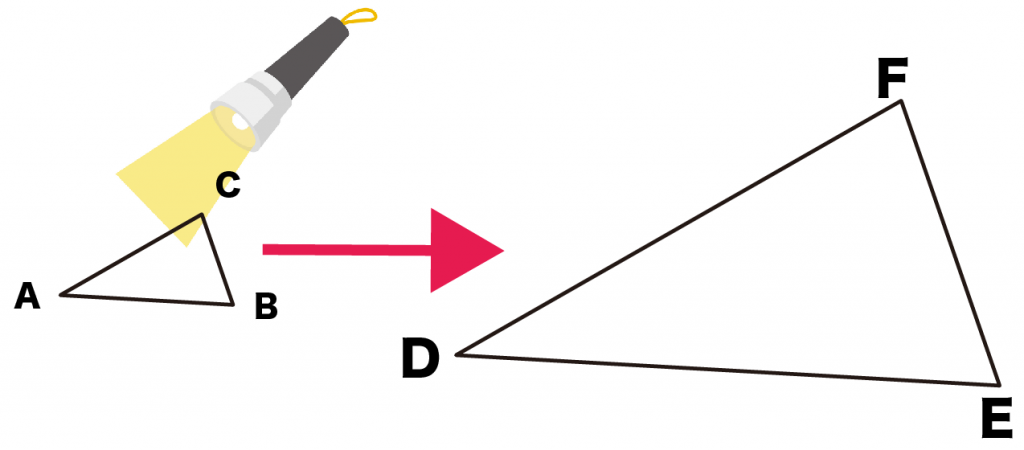
たとえば、ある△ABCをビックライトでむちゃくちゃでかくした。
その結果、
△DEFができたとしよう。
このとき、△ABCと△DEFは相似な図形である
っていえるんだ。
なぜなら、2つの三角形は拡大・縮小の関係にあるからね。
んで、相似比っていうのは、
相似な図形の対応する辺の比
のことなんだよ。
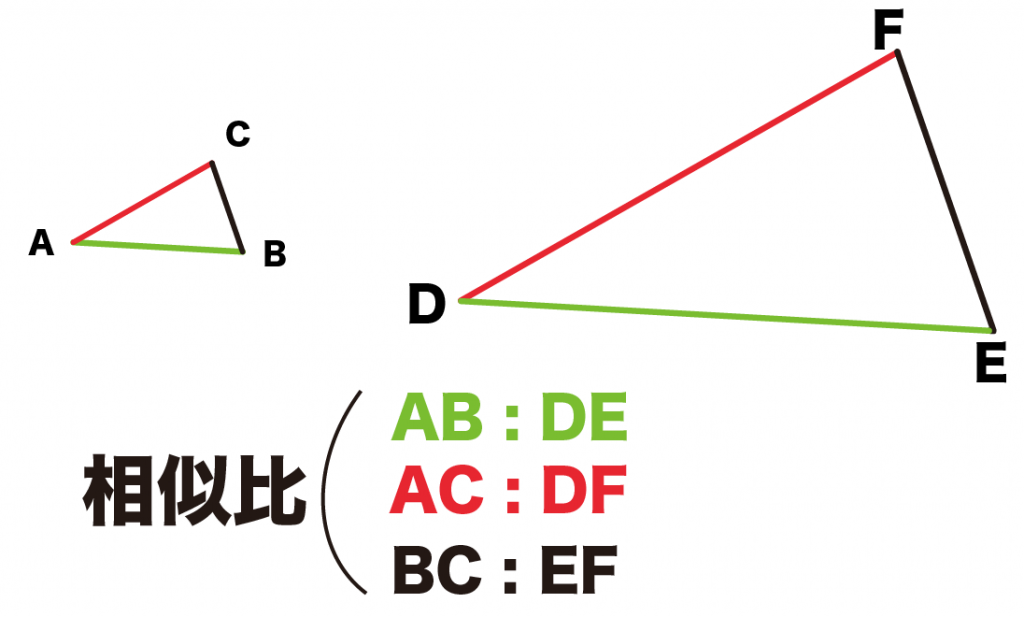
たとえば、△ABCと△DEFの例だったら、
- AB:DE
- BC:EF
- AC:DF
が相似比なんだ。
さあ、今回はこの相似比を求め方を解説していくよ。
相似比の求め方がわかる3つのステップ
相似比の求め方はつぎの3つのステップだよ。
- 対応する頂点をさがそう
- 対応する辺の長さを確かめよう
- 比にしてみよう
練習問題をいっしょにといてみよう。
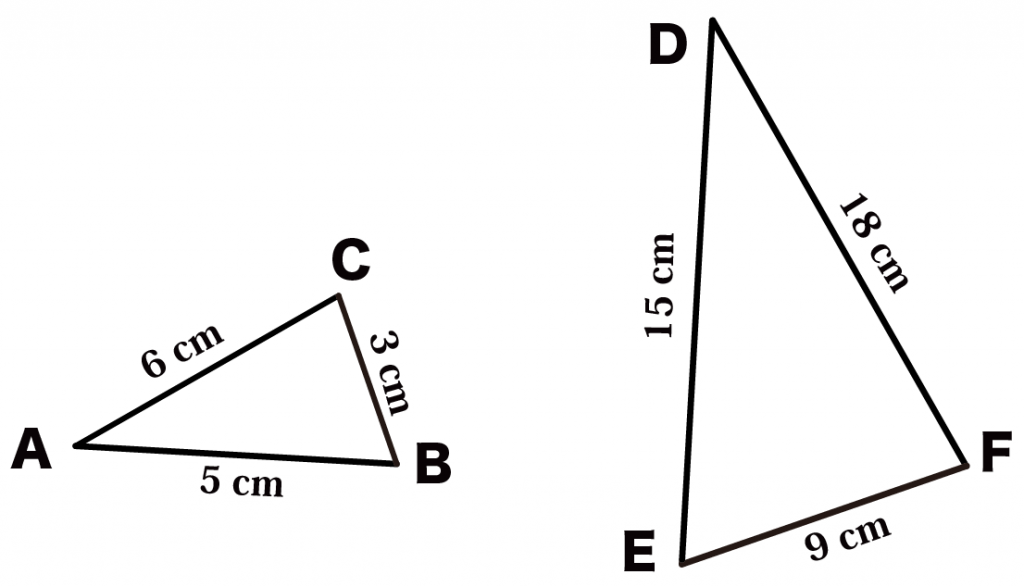
練習問題
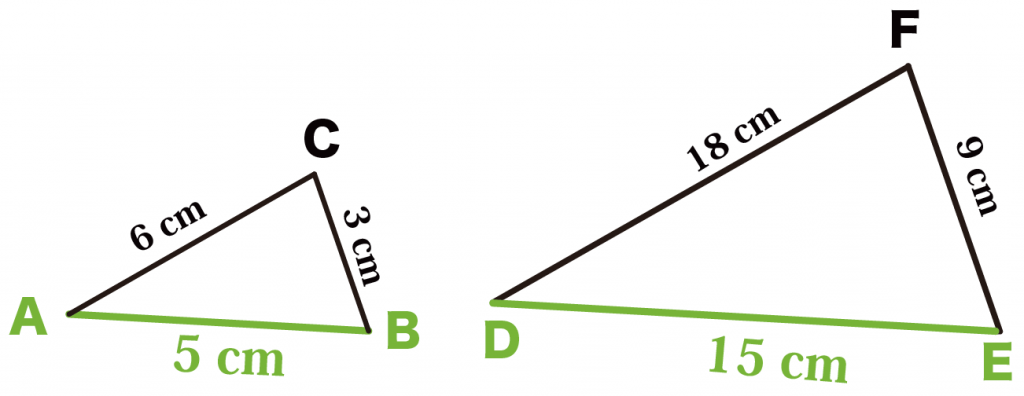
下の2つの三角形は相似である。相似比を求めよ。
Step1. 図形を頭の中で回転させよう
まず相似な図形の向きをそろえよう。
対応する頂点・辺がかさなるように回転させればいいんだよ。
練習問題をみてみよう。
このままだと対応する辺が見つけにくくない?
その理由は、三角形の向きが同じじゃないからだ。
だから、2つの三角形の向きを同じにしてあげよう!
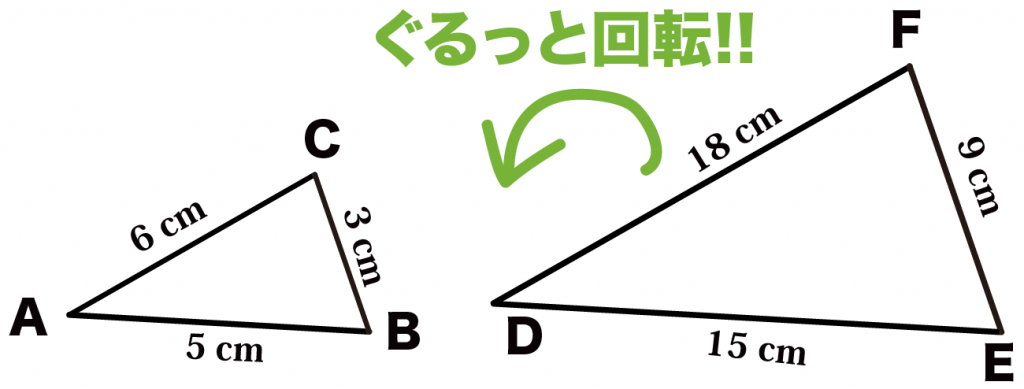
△DEFを左にぐるっとまわしてやればいいのさ。
そうするとこうなるよ。
これで対応する辺がみつけやすくなったね。
Step2. 対応する辺の長さを確かめる
つぎは、対応する辺の長さを確認してみて。
相似比は、
対応する辺の長さの比
だったよね??
だから、相似比を求めるためには、
2つの対応する辺の長さ
を知る必要があるわけ。
練習問題でいうと、
- 辺AB
- 辺DE
が対応する辺だね。
こいつらの長さはそれぞれ、
- 辺AB = 5
- 辺DE = 15
になってるね!
Step3. 相似比を求める
あとは相似比を求めるだけ。
相似比は、
対応する辺の長さの比
だったよね??
だから、もし、2つの相似な図形があったら、
対応する辺1 : 対応する辺2
の比を求めればいいわけ。
練習問題でいうと、△ABCと△DEFの相似比は、
AB : DE
を求めればいいね。
なぜなら、
この2つの辺が対応する辺同士だからね。
- 辺AB = 5
- 辺DE = 15
だったから、
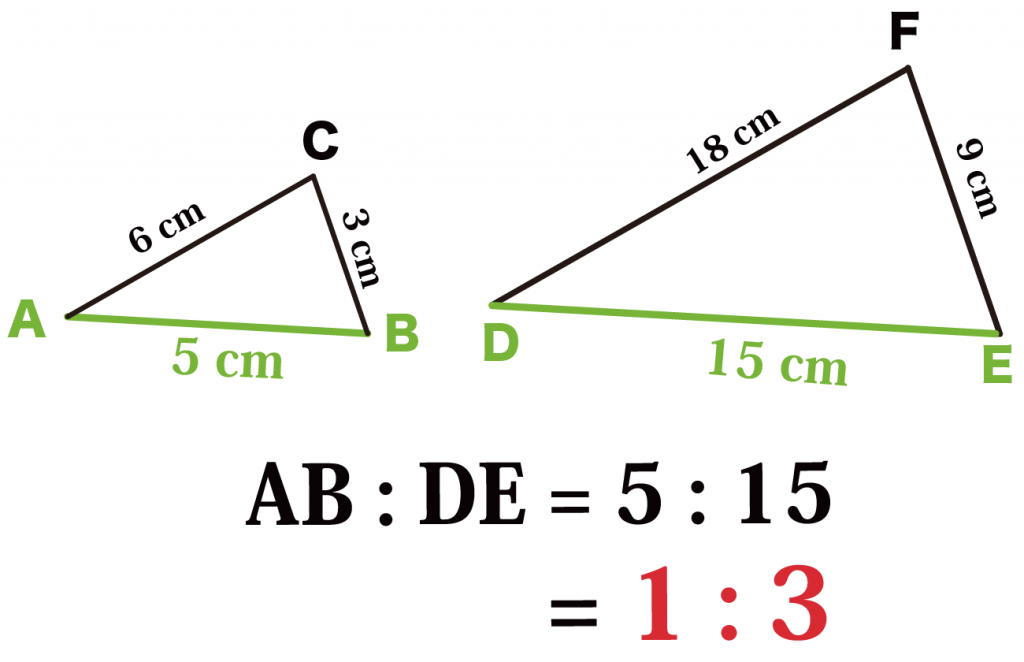
AB : DE
= 5: 15
= 1: 3
になる。
これが2つの三角形の相似比なんだ。
答えるときは一番簡単な整数で答えるよ。
そこだけ注意してね!
他の辺で計算しても1:3になるから安心して。
まとめ:相似の比の求め方は向きをそろえろ!
図形の相似比を求めるには回転させるのがカギ!
頭の中で回転させるイメージ力が必要。
回転させたらノートの余白に描いちゃおうね。
目ですぐに確かめられるから、解く時間を減らすこともできるよ。
相似比は基本的なことだからやり方覚えておいてね。
じゃ、また今度!
ぺーたー