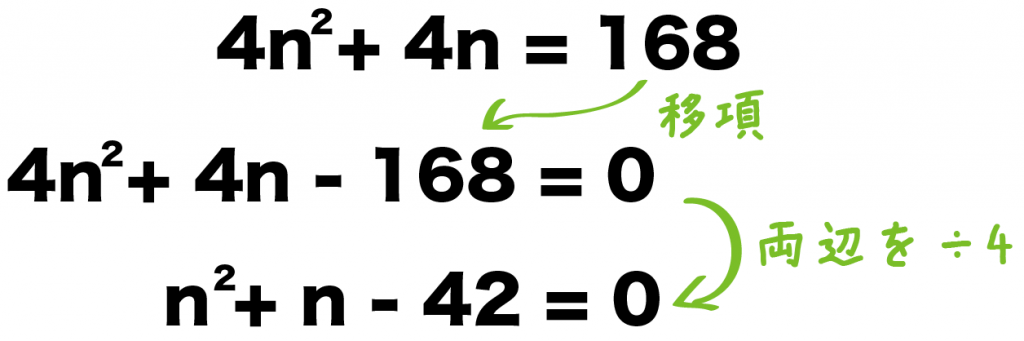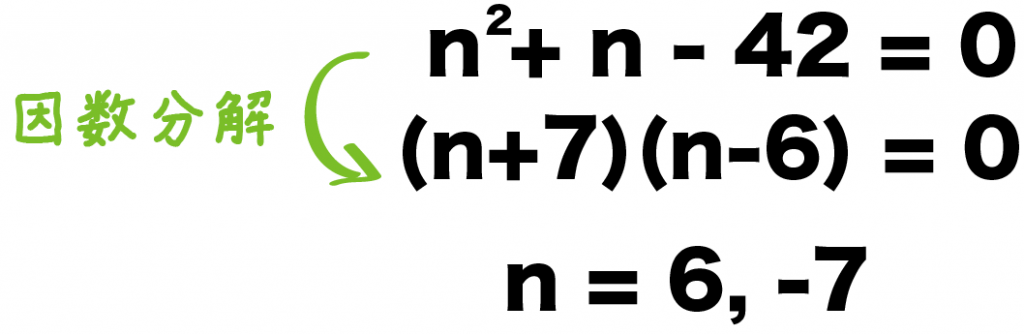【二次方程式の利用】文章問題の解き方がわかる4つのステップ
二次方程式の利用の文章問題の解き方??
こんにちは!この記事をかいているKenだよ。山の日は混むね。
二次方程式の解き方をたくさん勉強してきた。
因数分解をつかった解き方とか、
解の公式でとくやり方とかね。
ぶっちゃけ、
どんな二次方程式もとける自信あるよね??
だがしかし、中3数学の二次方程式はまだこれからなんだ。
二次方程式のゴールは、
二次方程式を文章問題でも使えるようになる
なんだよね。
そこで今日は、
二次方程式の利用の文章題の解き方
をわかりやすく解説してみたよ。
よかったら参考にしてみてね。
二次方程式の利用の文章題の解き方がわかる4ステップ
二次方程式の利用の解き方を解説していくよ。
つぎの練習問題をといてみよう。
練習問題
2つの連続する正の偶数の積が168になるとき、2つの偶数をそれぞれ求めなさい。
どんな文章題でも、4ステップでとけちゃうんだ。
- 求めたいものを文字とおく
- 二次方程式をたてる
- 二次方程式を解く
- 解を吟味する
Step1. 求めたいものを文字とおく
文章問題で求めたいものを文字でおこう。
辺の長さを求めたいときは「辺の長さ」、
ケーキの値段をだしたいときは「ケーキの値段」を文字でおけばいいのよ。
練習問題では、
積が168になる「2つの連続する正の偶数」
を求めたかったよね??
だから、「2つの連続する偶数を文字」であらわせばいいのさ。

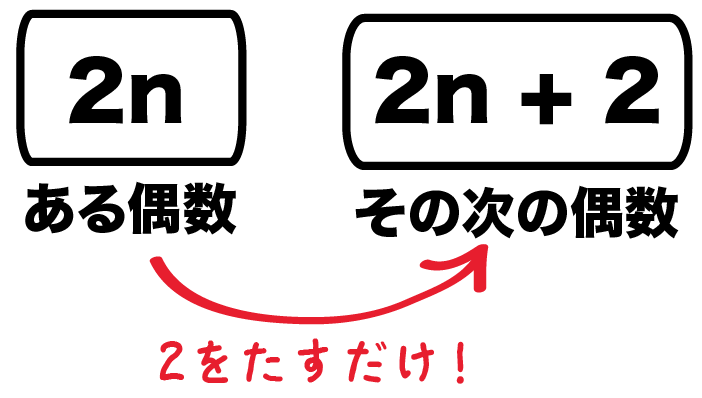
正の整数nで連続する偶数をあらわしてみよう。
※numberのnからきてるのさ。
ある偶数は、正の整数を2倍するとなるから、
2n
になるよね??
そのつぎの偶数はこいつより2大きいはずだから、
2n + 2
になるはず。
これが第1ステップだ。
Step2. 二次方程式をつくる
つぎは二次方程式をつくってみよう。
AがBになるとき
っていう文章をみつけて、「A=B」っていう方程式をたてればいいのさ。
例題では、
2つの連続する正の偶数の積が168になるとき
っていう文章に注目してみて。
ようは、
(2つの連続する正の偶数の積)= 168
っていう方程式をつくればいいんだね。
連続する2つの偶数はそれぞれ、
- 2n
- 2n+2
だったよね??
だから、2つの連続する偶数の積は、
2n (2n + 2)
になる。
こいつが「168」に等しくなるから、
2n (2n + 2) = 168
っていう方程式ができるね。
Step3. 二次方程式を解く
二次方程式を解いてみよう。
2次方程式の解き方はどれをつかってもいいよ。
因数分解でもいいし、解の公式をつかってもいい。
答えがでちゃえば問題ないわけだ。
練習問題の二次方程式は、
2n (2n + 2) = 168
だったよね??
左辺の()を分配法則ではずすと、
2n (2n + 2) = 168
4n^2 + 4n = 168
になる。
んで、移項して両辺を4でわってやると、
4n^2 + 4n – 168 = 0
n^2 + n – 42 = 0
になるね。
左辺の、
n^2 + n – 42
を因数分解してみると、
n^2 + n – 42
=(n +7)(n-6)
になるね。
よって、この二次方程式の解は、
n = 6, -7
だ。
Step4. 解を吟味する
二次方程式は無事とけたかな??
よかった!やったね!!
・・・・・・・・
・・・・・・・・
っていいたいところだけどね。
二次方程式の文章題の本番はこれからなんだ。
なぜなら、
その解が正しいか判断しなきゃいけないからね。
このことを数学界では、
解を吟味する
っていうんだ。
文字の条件を振り返ってみてね。
練習問題では、
- n = 6
- n = -7
がでてきたよね??
ここで、nは何かって振り返ってみると、
正の整数
だったよね??
えっと、、2つとも正の整数かなああ・・・
!!!?
あっ!
正の整数じゃないやつもいるやんけ!
そう。
n = -7
が条件にフィットしてないんだ。負の数だからね。
だから、この「n = -7」は適切じゃないってことがわかる。
したがって、2次方程式の解として正しいのは、
n = 6
だけだね。
よって、n = 6のとき、2つの連続する偶数は、
- 2n = 12
- 2n + 2 = 14
になる!
つまり、積が168になる連続する2つの正の偶数は、
- 12
- 14
の2つになるってわけ。
おめでとう!
これで二次方程式の文章題もマスターだね。
まとめ:二次方程式の利用の文章問題は解の吟味が大事
二次方程式の文章題はちょっとくせもの。
最後の最後に、
その解が問題として正しいのか??
を確かめなきゃいけないんだ。
最後まで気を引き締めていこう。
そんじゃねー
Ken