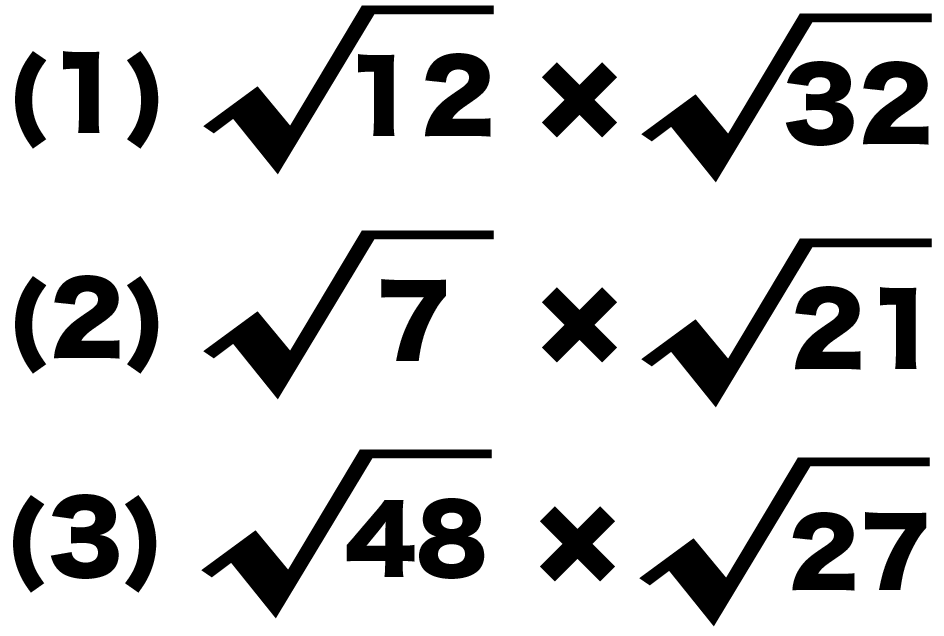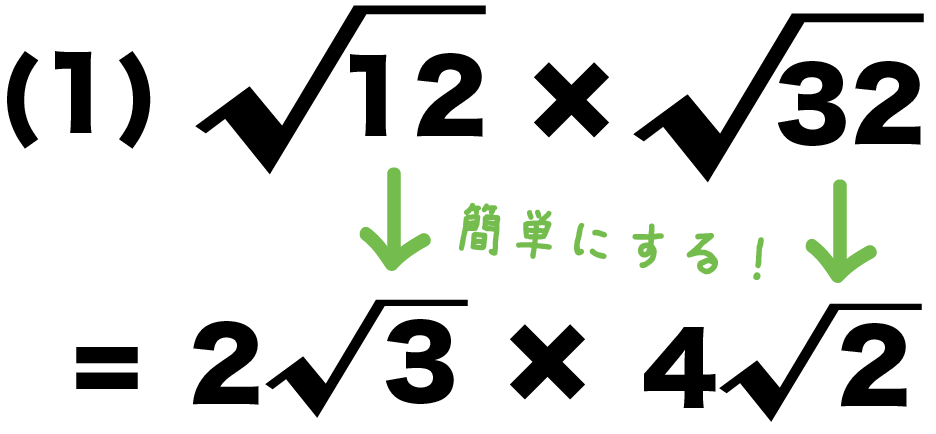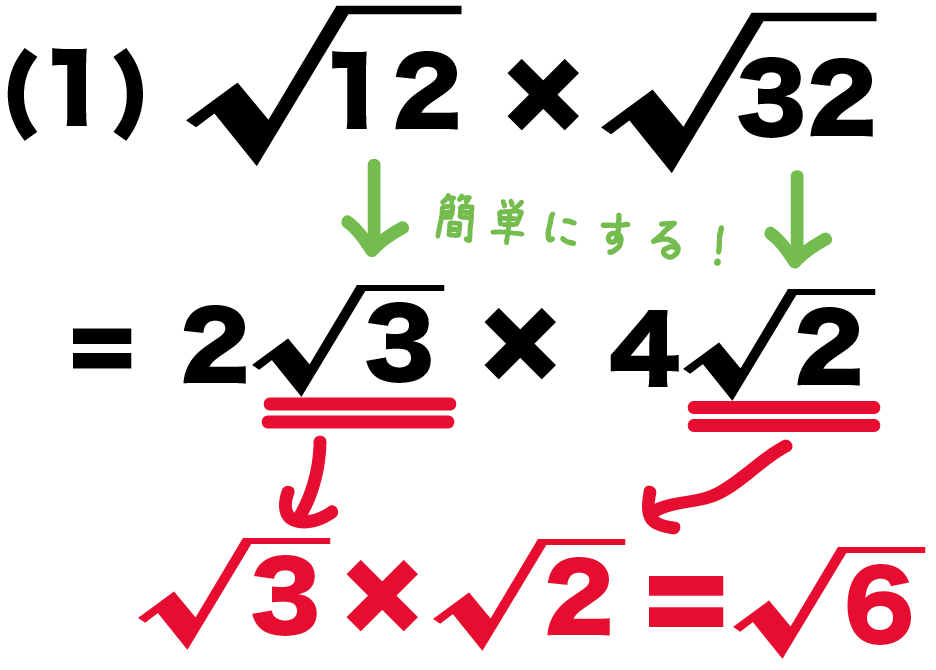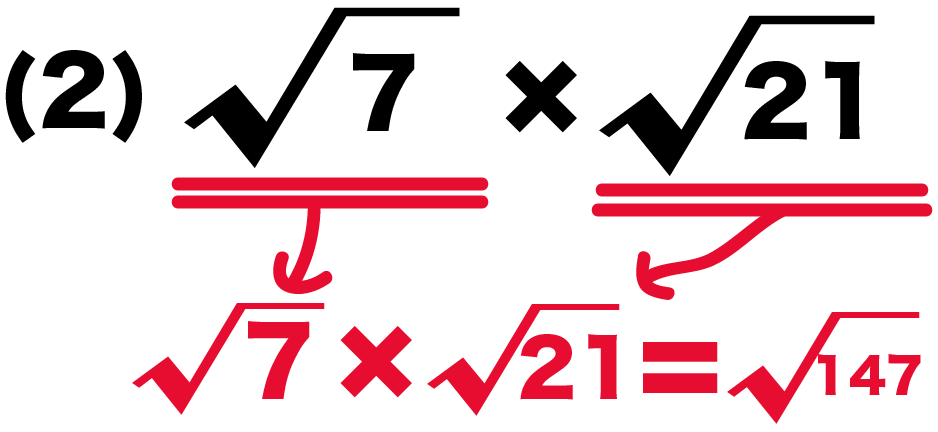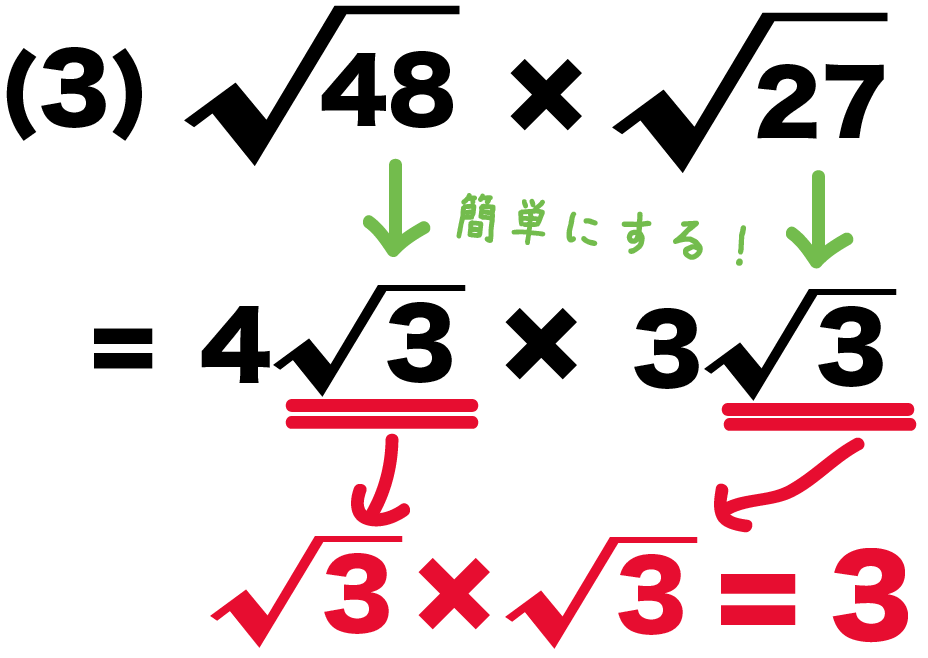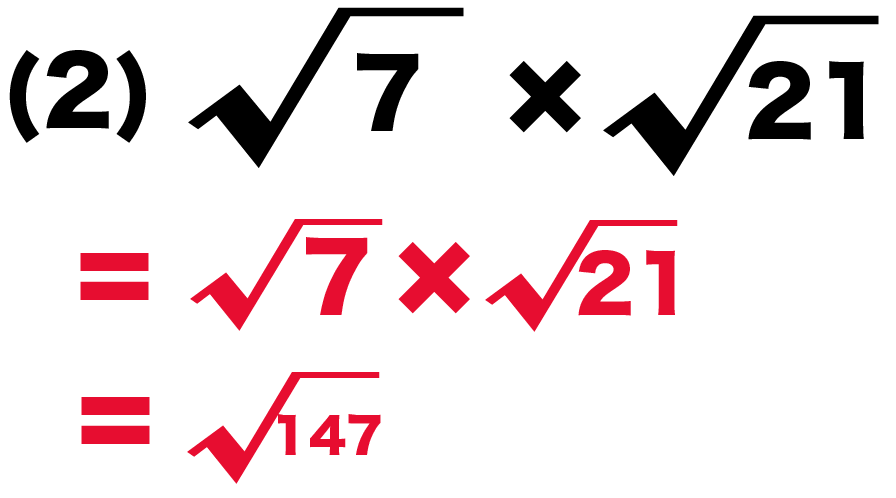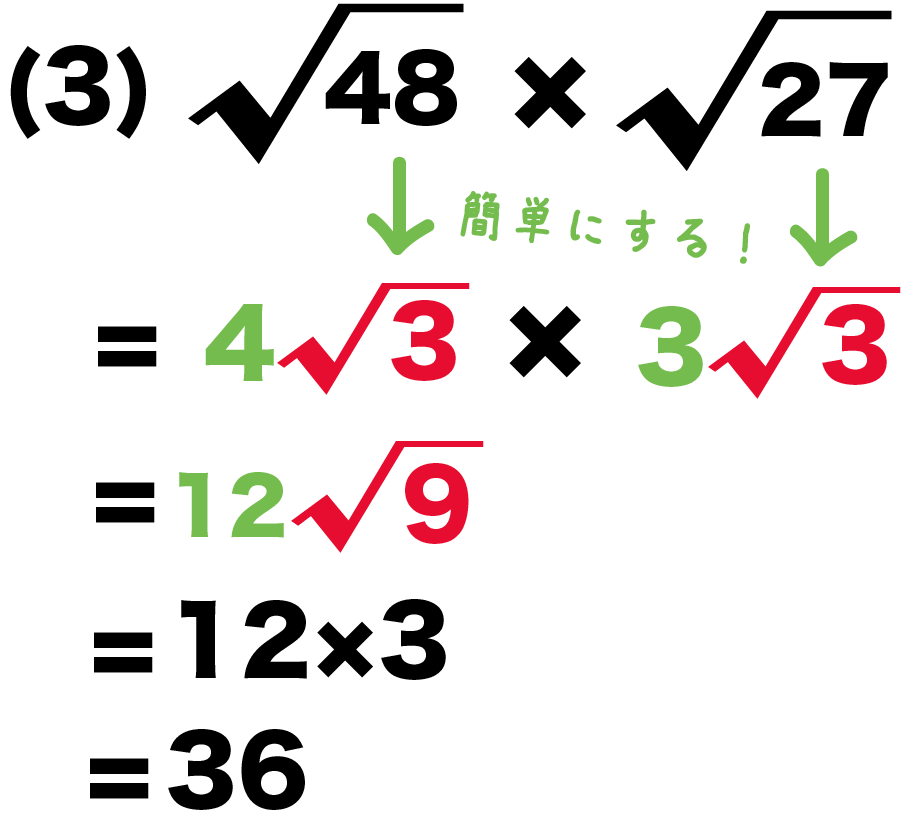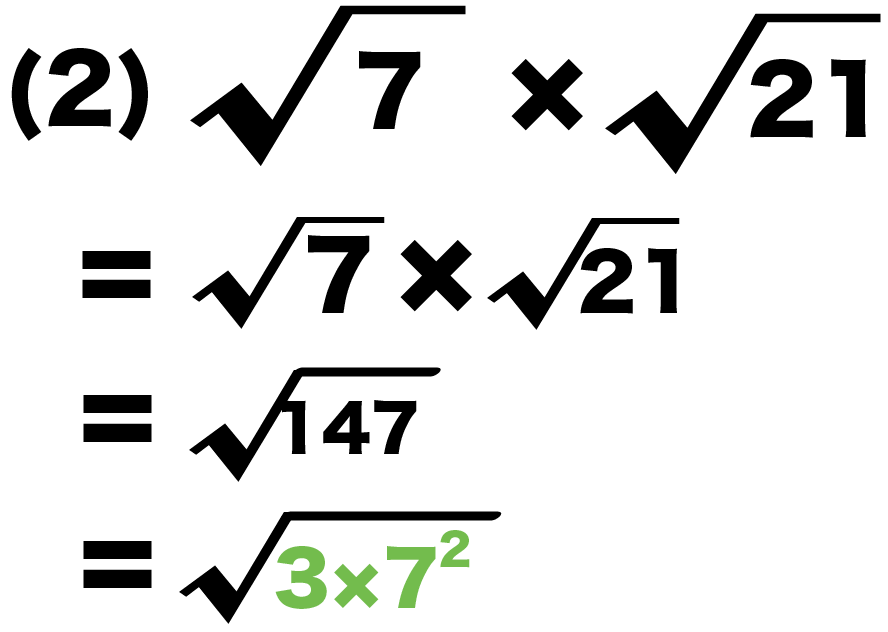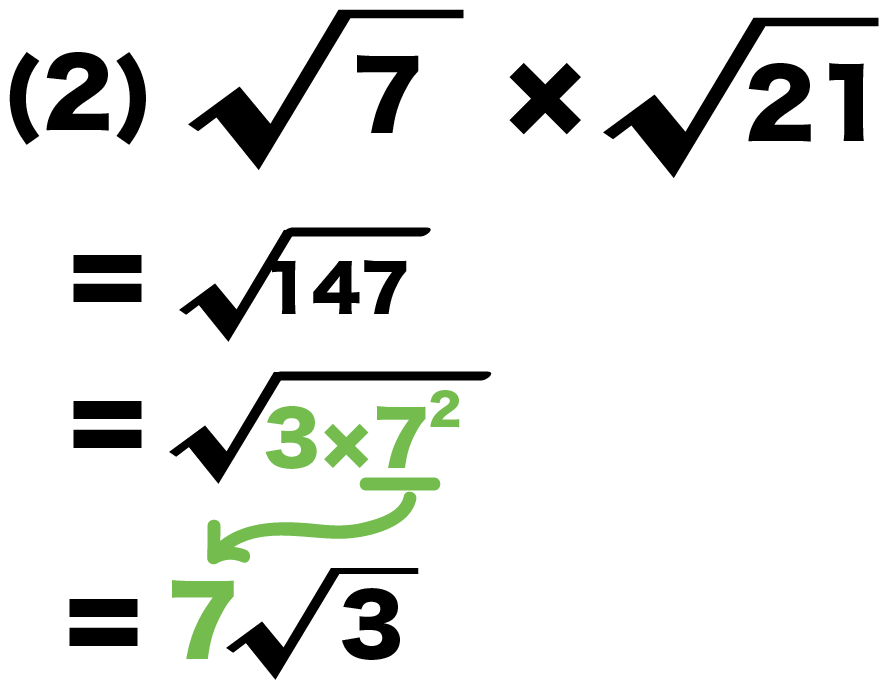平方根（ルート）の掛け算のやり方を知りたい！
こんにちは！この記事をかいているKenだよ。海につかりたいね。
平方根の計算にはいろいろある。
それこそ、
足し算、引き算、割り算、、、、、とか、もう、数えきれない。
そんななかに、
ルートの掛け算の計算
がある。
ルートの中身を掛け算するだけ
だったよね？？
そんなむずくなさそう。
だけどね、実際の計算問題だとそうはいかない。
そんなに世間は甘くないんだ。
そこで今日は、平方根の掛け算の計算方法を紹介していくよ。
平方根（ルート）の掛け算がわかる5ステップ
平方根の掛け算は5ステップで計算できるよ。
- ルートを簡単にする
- 整数同士をかける
- 平方根同士をかける
- くっつける
- ふたたびルートを簡単にする
えっ。5ステップもあるからダルいって！？？
ノンノン。
複雑にみえるけど、一瞬で計算できる。
安心してくれ。
例題をといていこう。
例題
つぎの平方根の計算をしてください。
(1) √12 × √32 (2) √7 × √21 (3) √48 × √27
Step1. 平方根を簡単にする
平方根を簡単にしてみよう。
「ルートを簡単にする」ってようは、
2乗になってる因数を取り出す
ってことだ。
⇒ くわしくは「平方根を簡単にする方法」をよんでみて
例として、(1)をみてみよう。
(1) √12 × √32
√12と√32をそれぞれ簡単にしてやると、
- √12 = 2√3
- √32 = 4√2
になる。
つぎは(2)の掛け算だ。
(2) √7 × √21
この平方根たちは簡単にできないね。
なぜなら、中身に2乗の因数がないからさ。
(3)も簡単にしてやると、
(3) √48 × √27
= 4√3 × 3√3
になるね！
Step2. ルート前の整数をかける
つぎは、整数の掛け算をしよう。
ルートはいったん無視していいや。
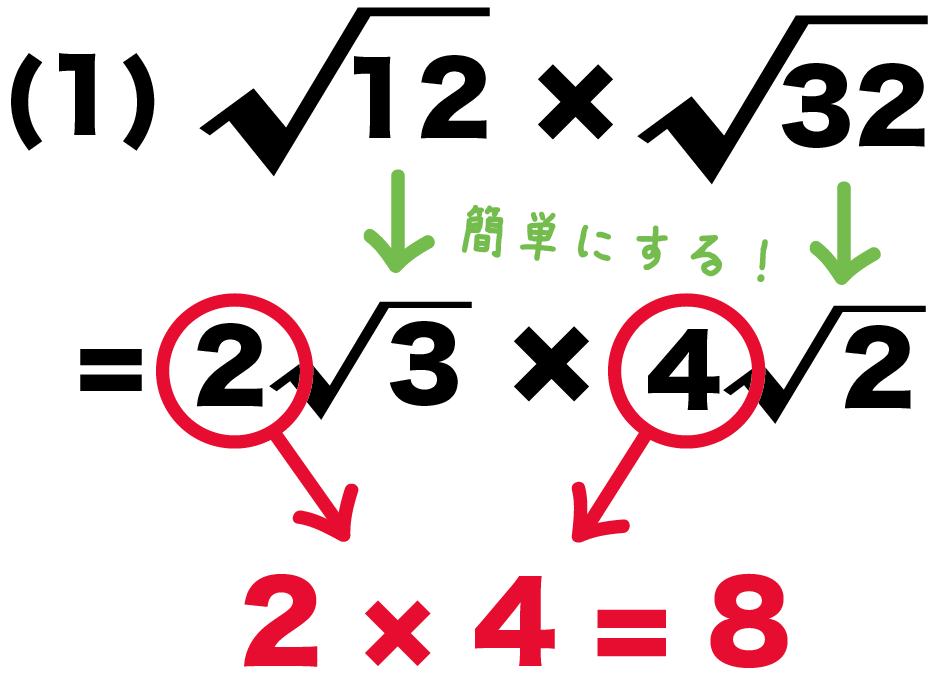
例題の(1)の計算でいうと、
(1) √12 × √32
= 2√3 × 4√2
だったよね？？
だから、整数の掛け算は、
2×4
= 8
になるね。
おなじように、(3)でも計算すると、
4×3
= 12
になるね！
ちなみに、(2)は整数がないからステイね。
Step3. 平方根部分を計算する
つぎは、平方根の掛け算をするよ。
ルートを1つにして中身だけ計算しちゃう
だったよね？？
例題でもおなじさ。
(1) √12 × √32
= 2√3 × 4√2
の平方根部分の掛け算は、
√3 × √2
= √6
になるね！
例の(2)もおなじ。
平方根の掛け算の基本をつかって計算すると、
√7×√21
= √147
になるね！
例題の(3)の、
√48 × √27
= 4√3 × 3√3
でもおなじさ。
平方根の掛け算をしてやると、
√3×√3
= 3
になるね。
Step4. くっつける
さっき計算した、
- 整数部分
- ルート部分
をくっつけてやろう。
ピタっとくっつけるだけでいいんだ。
例題の(1)だったら、
(1) √12 × √32
= 2√3 × 4√2
= 8√6
になるね。
(2)は平方根だけの掛け算だからステイ。
(3)の平方根の計算は、
√48 × √27
= 4√3 × 3√3
= 12×3
= 36
になるね！
Step5. ルートを簡単にする
最後に、ルートをもっと簡単にできるか挑戦。
ルートの中身はいちばん簡単にすべきだからね。
例題の計算をみてみると・・・
・・・ん！？
(2)のルートはもっと簡単にできそうじゃないか？？
中身の147を素因数分解すると、
147 = 3×7の2乗
になってる。
因数の7が2乗になってるじゃん？？
最終的に、(2)の計算問題は、
√7×√21
= √147
= 7√3
になるね。
こんなかんじで、
ルートをもう一度簡単にできるか
チェックしてみよう！
まとめ：平方根の掛け算は簡単にしてから！
平方根の掛け算のコツは、
ルートを簡単にして、整数と平方根をわけるってこと。
そのほうが計算が楽。
じゃんじゃんルートの掛け算していこう。
そんじゃねー
Ken
