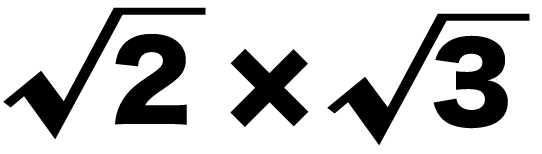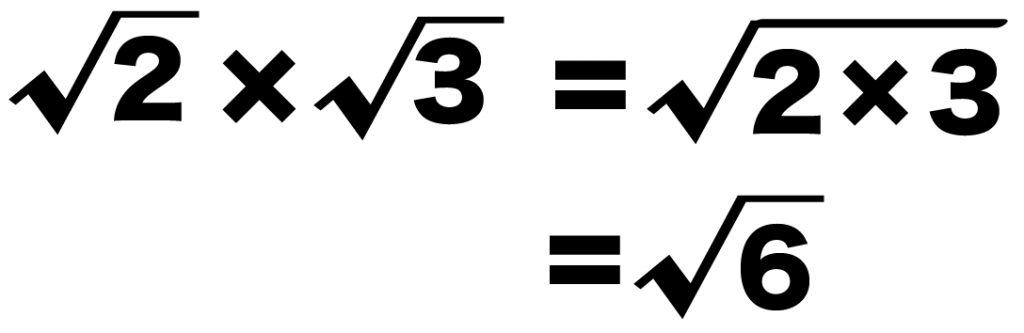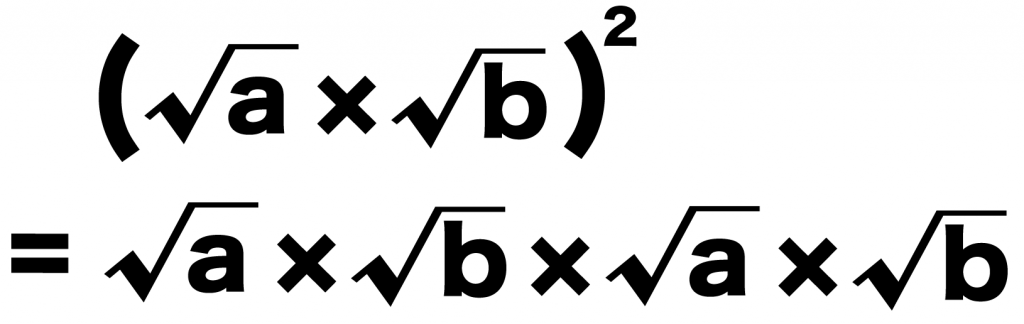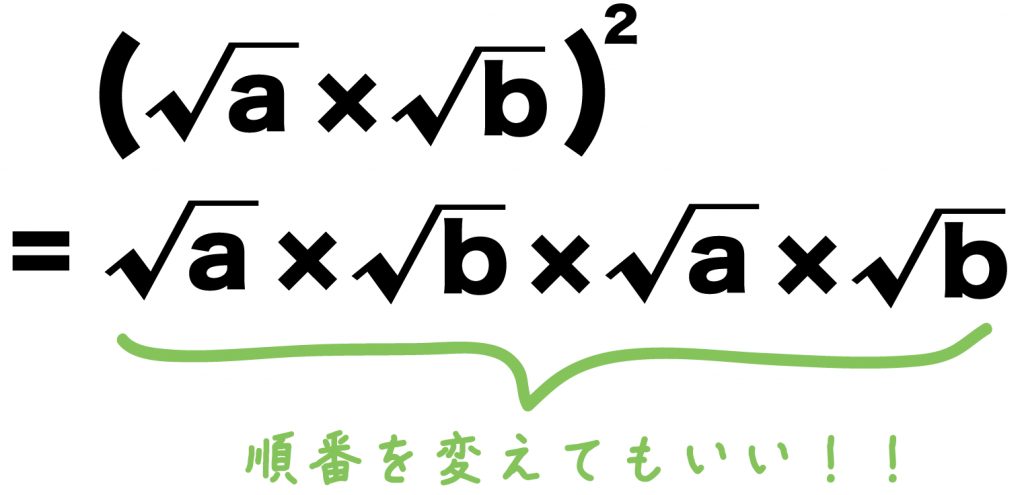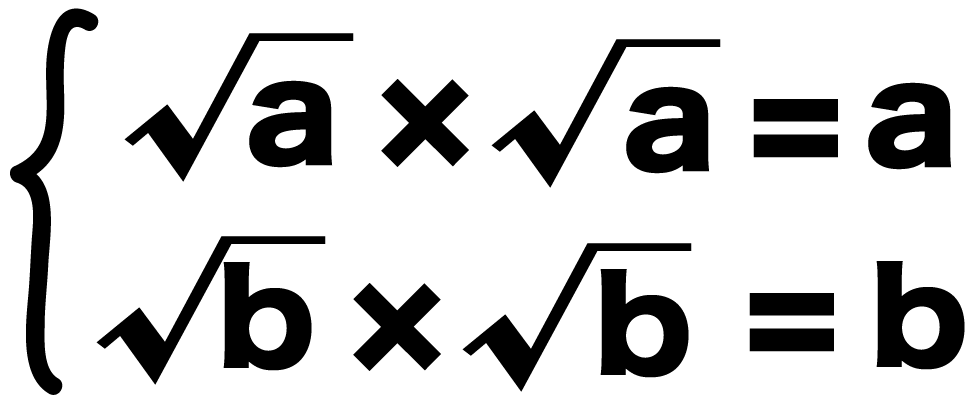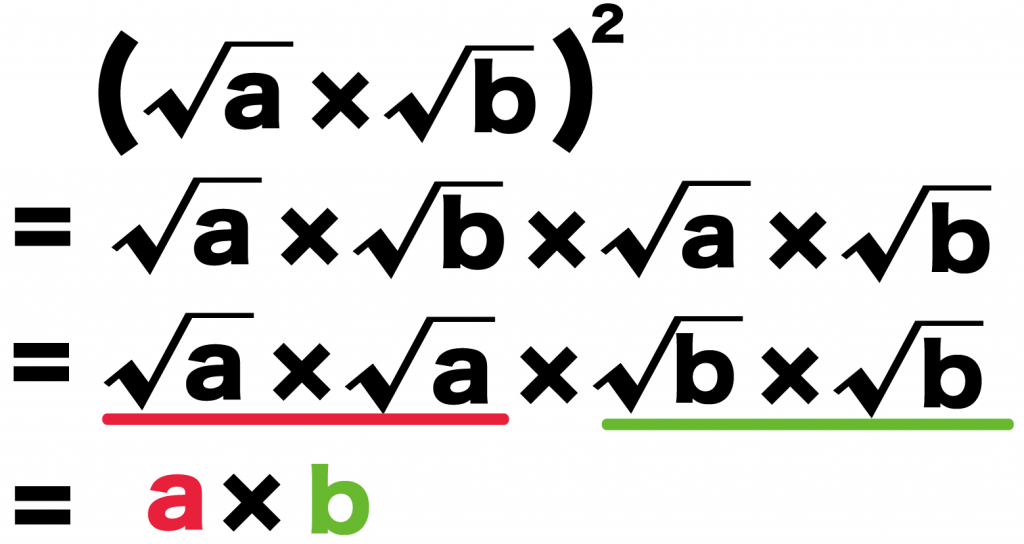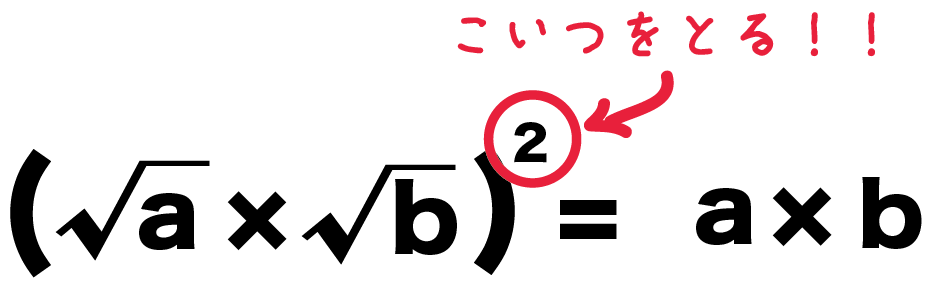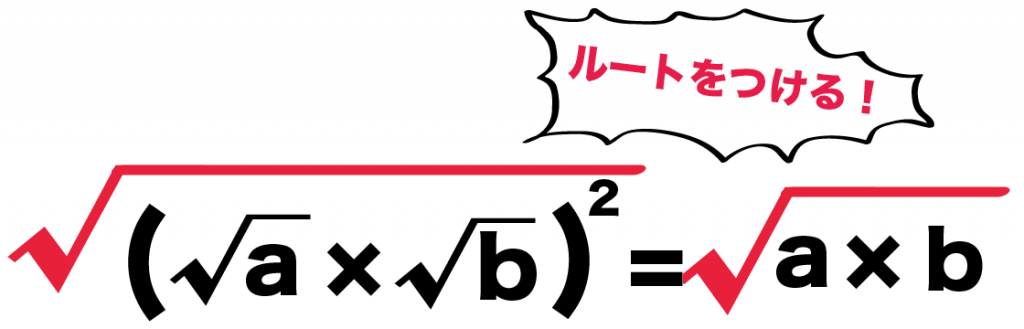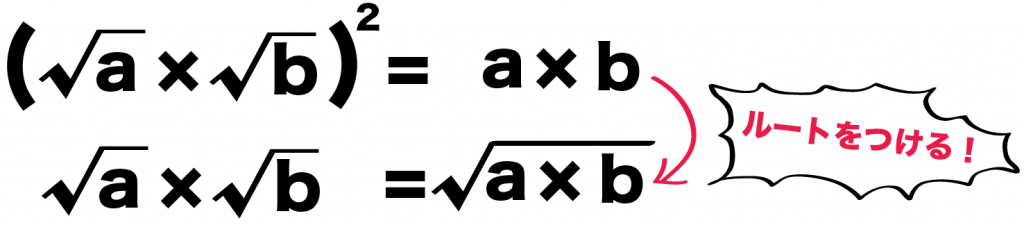【平方根の計算】3分でわかる!ルートの掛け算の基本
平方根(ルート)の掛け算ってどうやるの!?
こんにちは!この記事をかいてるKenです。ハットかぶりたいね。
平方根の計算のなかでいちばんとっつきやすいのは、
掛け算
だ。
なぜなら、
平方根の計算の中でいちばんルールが簡単だからさ。
そのルールとは、
ルート同士の掛け算では中身を掛け算して一緒のルートの中にいれる
ってやつなんだ。
だから、たとえば、
(ルートa)×(ルートb)
っていう平方根の掛け算があったとしたら、
ルートab
になるってわけだ。
平方根(ルート)の掛け算は意外と簡単じゃん!?
この計算の基本ルールを使えばルートの掛け算は簡単だ。
とりあえず、
ルートの中身をかけちゃえばいいからね。
たとえば、
(ルート2)×(ルート3)
っていう掛け算の計算があったとしよう。
さっき勉強した掛け算の基本ルールを使うと、
(ルート2)×(ルート3)
= ルート(2×3)
= ルート6
になるね!
ルートの中身をかけあわせて、ルートを1つにするだけだから、
むちゃくちゃ簡単だね。
平方根の掛け算バンザイ!
なぜ、平方根の掛け算の計算は簡単にでちゃうの??
でもさ、
なんで平方根の掛け算ってこんなに簡単なのかな??
もうちょっと複雑でもいいなあー
って不満があるかもしれない。
せっかくだから、
なぜ、ルートの掛け算の基本ルールは使えるのか??
ってことを勉強してみよう。
具体的には、掛け算の基本ルールの、
(ルートa)×(ルートb)= ルートab
を証明してみるよ。
つぎの4ステップを踏めば大丈夫!
Step1. とりあえず2乗してみる
まずは、
(ルートa)×(ルートb)
を2乗してみよう。とりあえずね。
こいつらを2乗してみると、
{(ルートa)×(ルートb)}^2
= (ルートa)×(ルートb)×(ルートa)×(ルートb)
になるね!
Step2. 交換法則で順番をチェンジ
つぎは、
交換法則で掛け算の順番をチェンジしよう。
交換法則って簡単にいうと、
掛け算や足し算の順番を変えてもいいよ
っていう法則だったね。
⇒くわしくは交換法則の記事をよんでみてね
さっき2乗してできた式に注目してくれ。
{(ルートa)×(ルートb)}^2
= (ルートa)×(ルートb)×(ルートa)×(ルートb)
じつは、この掛け算の式で交換法則をつかうと、
この2行めの掛け算の順番をかえてもいい
っていうことになるんだ。
だから、ルートが消えるように都合よく掛け算の順番をかえてやると、
{(ルートa)×(ルートb)}^2
= (ルートa)×(ルートb)×(ルートa)×(ルートb)
= (ルートa)×(ルートa)×(ルートb)×(ルートb)
になるね!
Step3. 掛け算する
つぎは、順番を入れ替えた状態でルートの掛け算してみよう。
ここでのポイントは、
ルートの中身が同じ平方根を2回かけるとルートがはずれる
ってことだ。
つまり、
- (ルートa) × (ルートa) = a
- (ルートb) × (ルートb) = b
になるってことさ。
こいつらを使ってさっきの計算をすすめてやると、
{(ルートa)×(ルートb)}^2
= (ルートa)×(ルートb)×(ルートa)×(ルートb)
= (ルートa)×(ルートa)×(ルートb)×(ルートb)
= a×b
になるね!
Step4. 「2乗をはずす」
最後に、
最初にとりあえず2乗した「2乗」をとりのぞこう!
いったん、もとにもどしてやればいいんだ。
さっきの計算式では、
{(ルートa)×(ルートb)}^2 = a×b
になっていたわけだ。
こいつの左辺の、
{(ルートa)×(ルートb)}^2
の2乗をとっぱらえばいいんだよ。
2乗の取り方は簡単!
左と右の両方にルートをかぶせちまえばいいんだ。
こんな感じでね↓↓
左のルートは中身が2乗になってるね??
こういうときは、2乗とルートがともにきえてなくなるから、
ルート{(ルートa )×(ルートb)}^2
= (ルートa )×(ルートb)
になるんだ。
よって、
(ルートa )×(ルートb)= ルート(a×b)
になるね!
おめでとう。
これでルート掛け算の基本法則を証明できたね。
まとめ:平方根(ルート)の掛け算は中身をかけるだけ!
ルートの掛け算??
びびることはない。
ルートとルートを1つにしちゃって、
中身をかけあわせればいいんだ。
平方根の計算は簡単だから、
なぜ、平方根の掛け算が計算できちゃうのか??
っていうことまでおさえておこう。
そんじゃねー
Ken