中3数学の式の値の計算の問題がわからない！？
こんにちは！この記事をかいているKenだよ。公園をふらっとしたね。
中3数学ではたくさんの計算問題をとかされるよ。
その中の問題の1つに、
式の値の計算
ってやつがあるんだ。
これはぶっちゃけいうと、
文字式のなかの文字に数字を入れたらどうります？？
っていう問題だ。
たとえば、つぎのような問題だね。
例題
x = 10, y = 2のとき、つぎの式の値を求めなさい。
(2x+3y)(2x-3y) – (x-2y)(x-5y) + 10
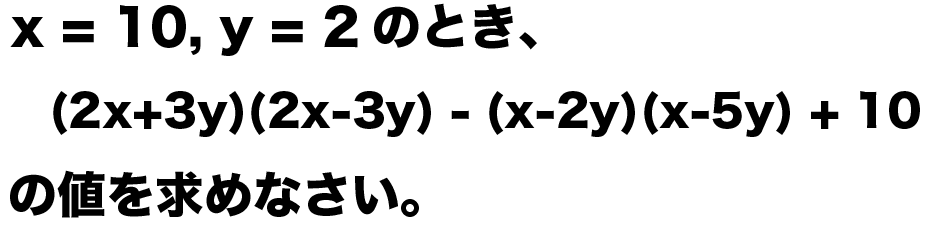
今日はこのタイプの、
式の値の計算の問題
を3ステップで解説していくよ。
解き方がわからないときに参考にしてみてね。
式の値の計算の問題がわかる3つのステップ
さっきの例題をいっしょにといていこう。
例題
x = 10, y = 2のとき、つぎの式の値を求めなさい。
(2x+3y)(2x-3y) + (x-2y)(x-5y) + 10
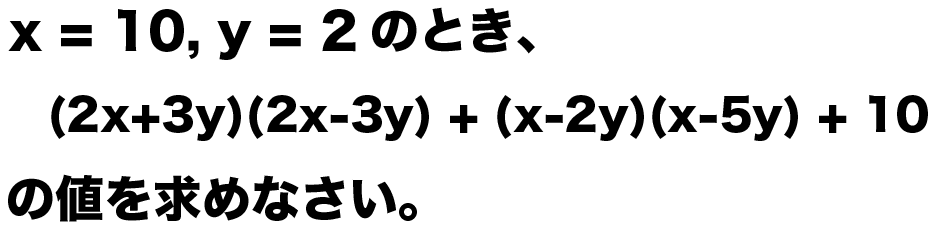
この手の問題はつぎの3ステップでとけちゃうよ。
- 展開する
- 同類項をまとめる
- 数を代入する
Step1. 展開する
とりあえず、与えられた文字式を展開しちゃおう。
展開には乗法公式をつかってあげると便利だよ。てか計算がはやくなるね。
例題の文字式は、
(2x+3y)(2x-3y) – (x-2y)(x-5y) + 10
だったよね？？
この文字式にたいしては、
- 和と差の公式
- (x+a)(x+b)の公式
の2つがつかえそうだ。
さっそく乗法の公式で計算してみると、
(2x+3y)(2x-3y) + (x-2y)(x-5y) + 10
= 4x² – 9y² +(x² -7y +10y² ) +10
になるね！
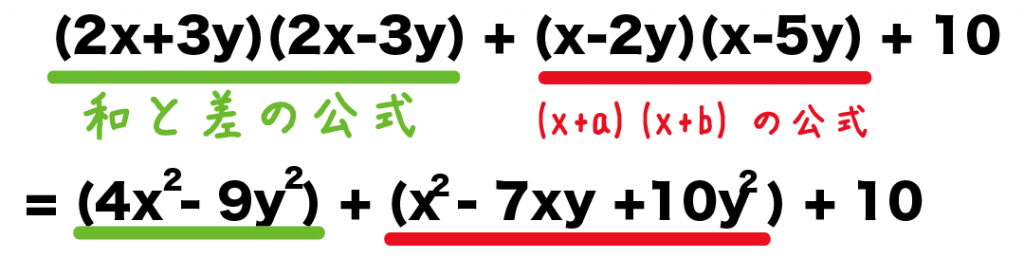
これが第1ステップさ。
Step2.同類項をまとめる
つぎは展開したやつらのなかで同類項をまとめてみよう。
つまり、
文字と次数がおなじ項同士の足し算引き算をしてあげるってことさ。
例題でも、同類項をまとめてやると、
(2x+3y)(2x-3y) + (x-2y)(x-5y) + 10
= 4x² – 9y² +(x² -7y +10y² ) +10
= 5x² + y² – 7xy + 10
になるね！
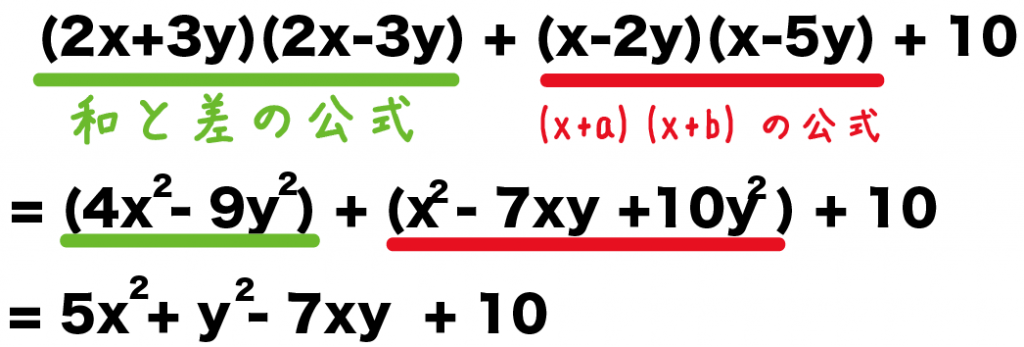
Step3. 数字を代入する
最後に数字を文字に代入してみよう。
xならxに、yならyに、値をぶちこんでやればいいんだ。
例題では、
- x = 10
- y = 2
だったね？？
こいつらを同類項をまとめたあとの式に代入してやると、
5x² + y² – 7xy + 10
= 5×(10)² + (2)² – 7×10×2 + 10
= 374
になるね。
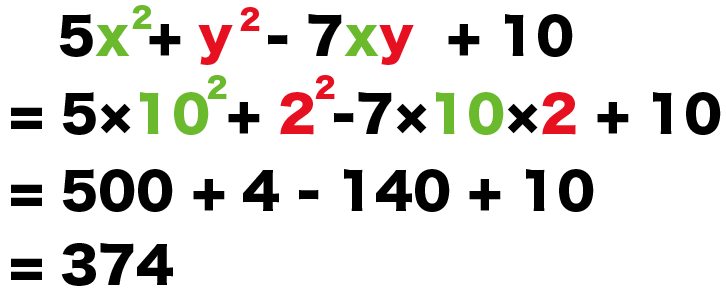
おめでとう！
これで式の計算の値も求めることができたね！
まとめ：式の計算の値は展開公式でどうにかなる！！
式の計算の値の問題はシンプル。
というか、
展開の公式さえおぼえていればどうにかなるね。
だって、
展開してきれいにととのえて文字を代入するだけだからね。
問題をといて代入になれていこう！
そんじゃねー
Ken
