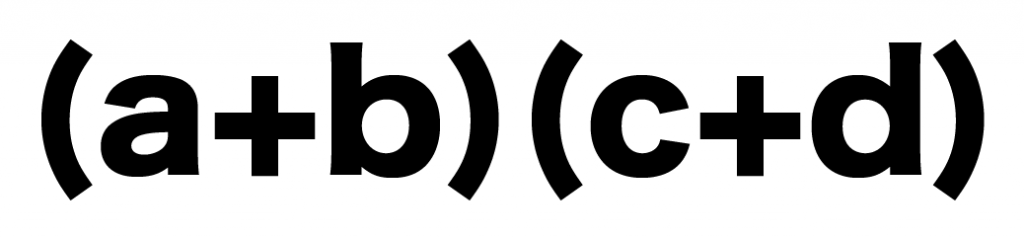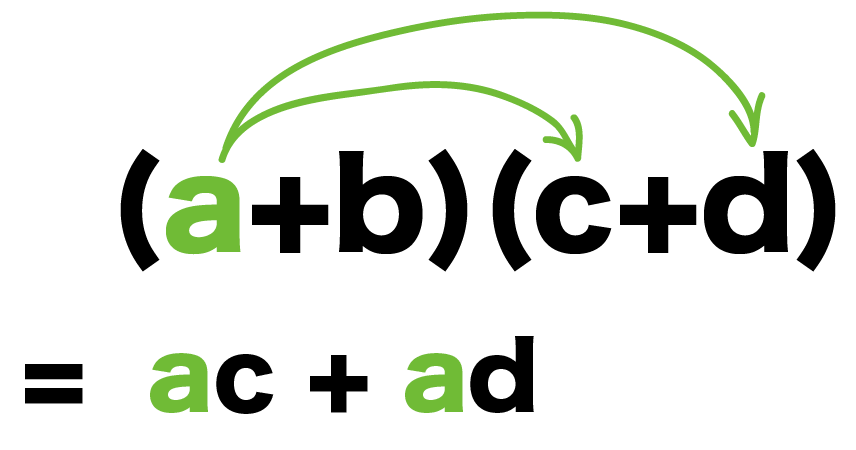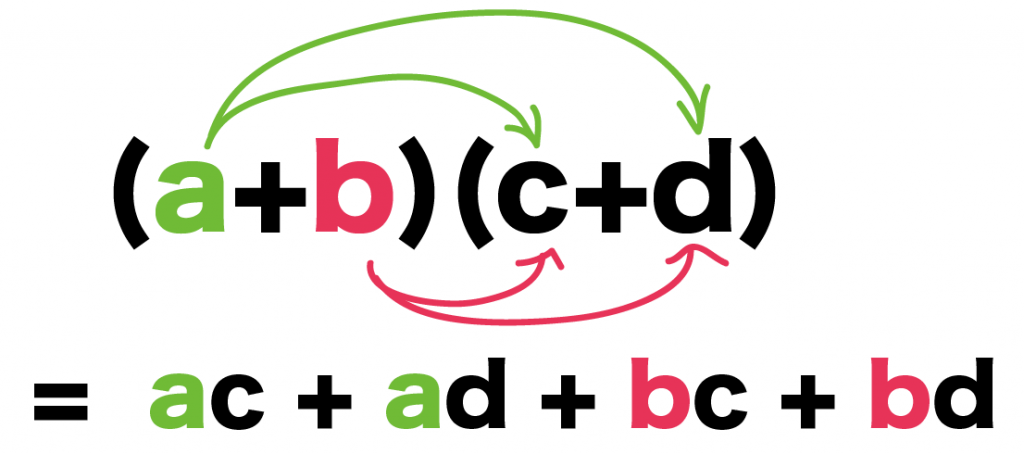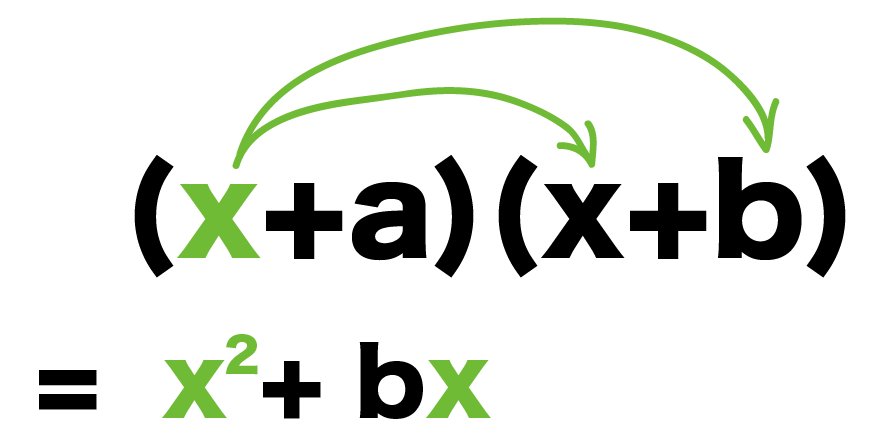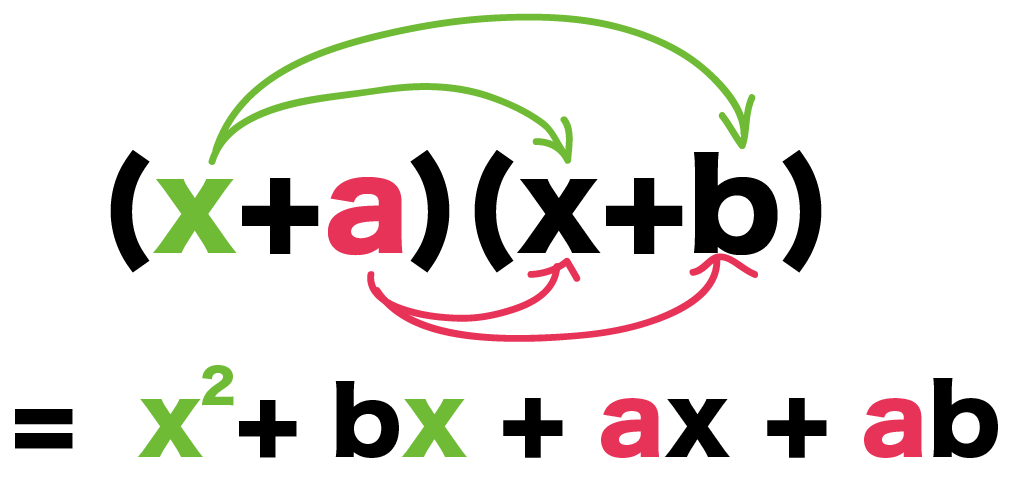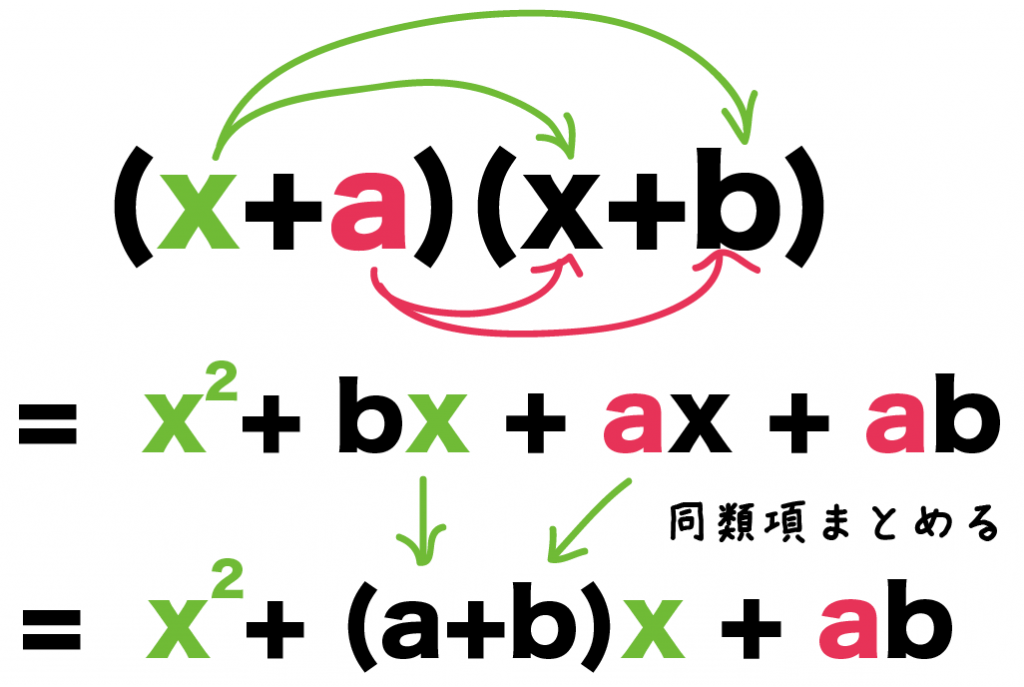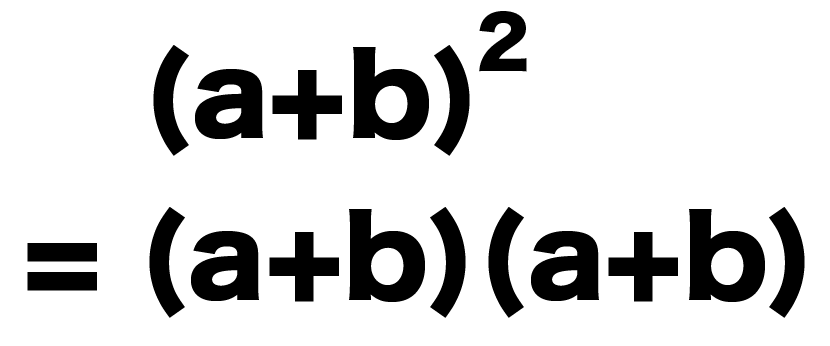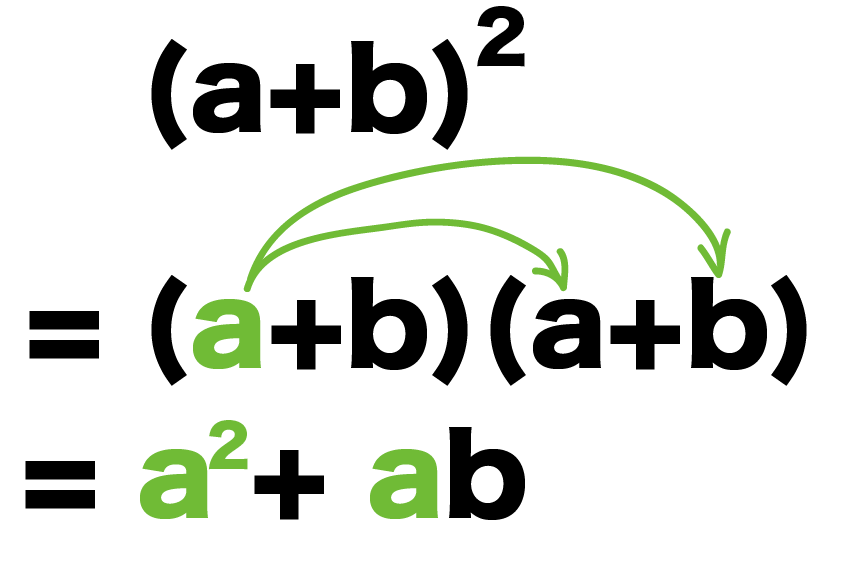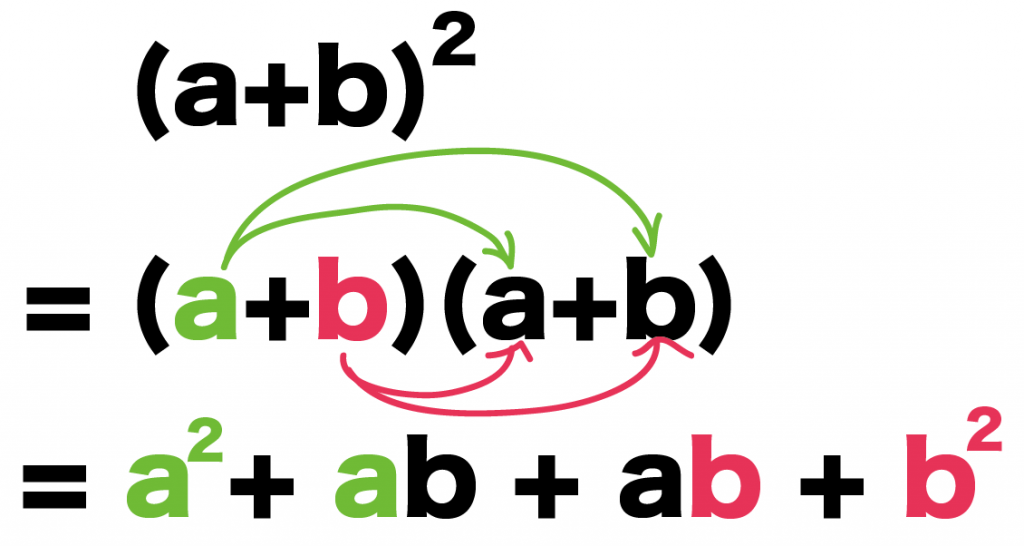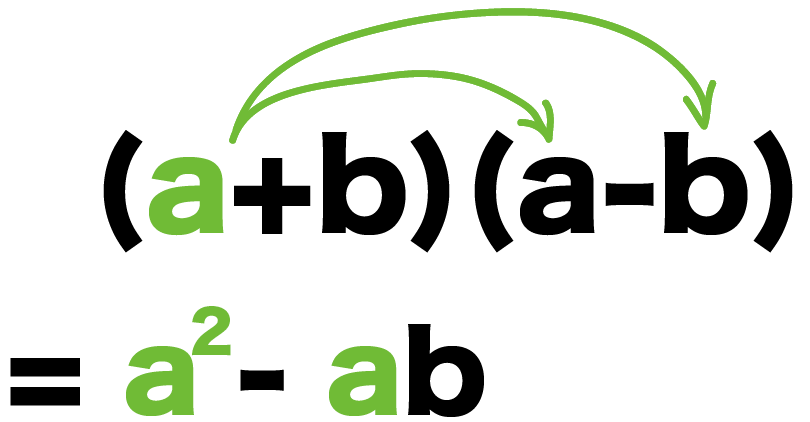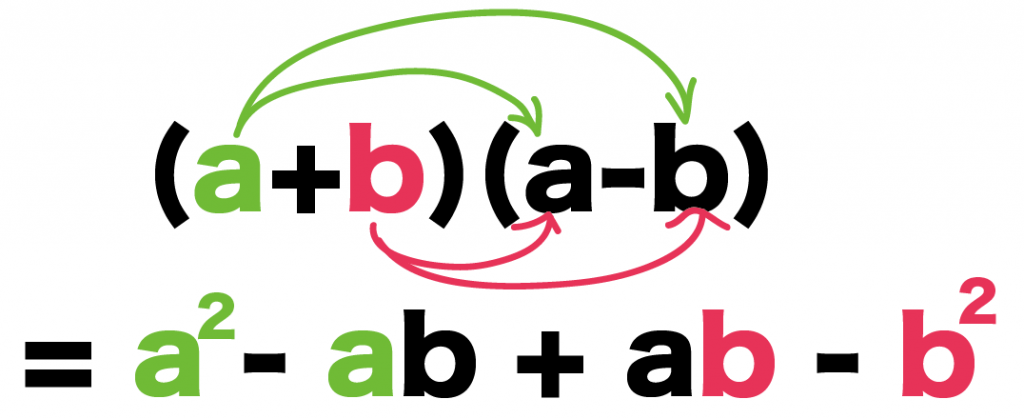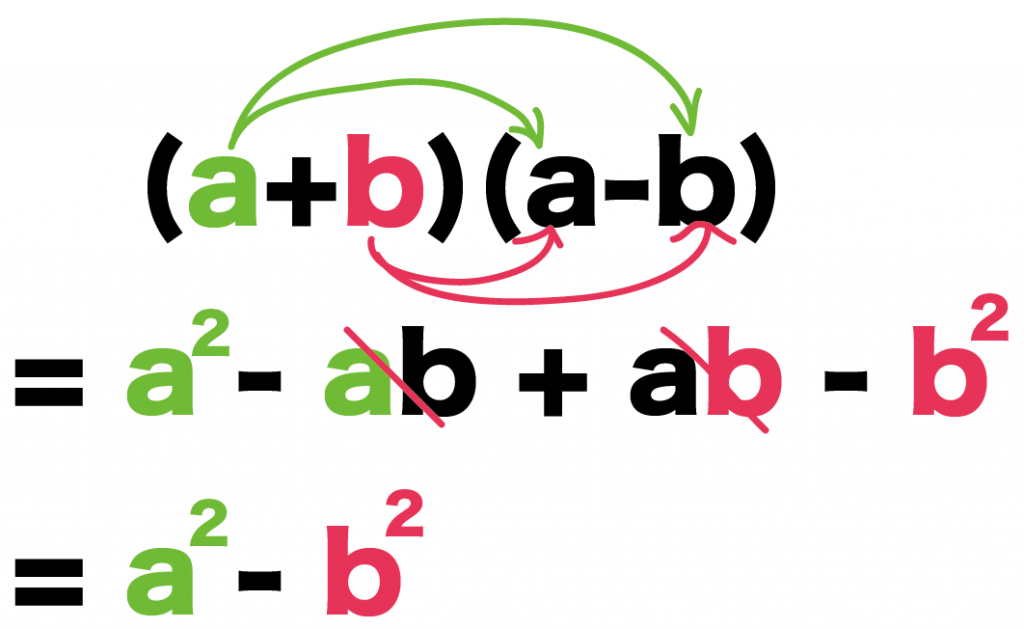【簡単証明】乗法の公式はなぜ使えるんだろう??
乗法の公式はなんで使えるんだろう??
こんにちは!この記事をかいているKenだよ。シロップに要注意だね。
中学数学でならう公式は3つある。
- (x+a)(x+b)の展開
- 平方の公式
- 和と差の積の公式
ぶっちゃけ公式覚えてれば大丈夫。
もうね、楽勝。
公式通りに計算すればいいからね。
だけどさ、
乗法公式はなんでつかえるんだろう??
ぶっちゃけ怪しいんだよね。
知らないおじさんについていくみたいでさ。
そんな疑問を解消するために今日は、
乗法公式(式の展開の公式)はなぜつかえるのか??
を解説していくよ。
よかったら参考にしてみてね。
3分でわかる!乗法の公式の3つの証明
式の展開の公式を証明するために使うのはただ1つ。
それは、
さ。
えっ。分配法則なんて忘れただって??
そうだね。
分配法則とはずばり、
()の外側の数字や文字を()内の項に順番にかけて展開すること
だよ。
たとえば、
(a+b)(c+d)
っていう計算式があったとしよう。
分配法則つかえば一瞬で展開できるんだ。
まず、「a」をうしろにある()内の項にそれぞれかける。
そして、たす。
(a+b)(c+d)
= ac + ad
つぎは「b」をうしろの()内の項にかけて、たしてやるんだ。
つまり、
「b」を「c」と「d」にかけてたせばいいのさ。
よって、
(a+b)(c+d)
= ac + ad +bc + bd
になるね。
この分配法則が使えればOK。
乗法公式も証明できちゃうよ。
(x+a)(x+b)の展開公式の証明
さっそく一つ目の、
(x+a)(x+b)
を証明してみよう。
分配法則で展開してやればいい。
まず、「x」をうしろの()の2つの中にかける。
(x+a)(x+b)
= x^2 + bx
つぎは、「a」をうしろの2つの項にかけてたしてやる。
すると、
(x+a)(x+b)
=x^2 + bx +ax +ab
になるね。
あとは同類項「bx」、「ax」をまとめるだけさ。
(x+a)(x+b)
= x^2 + bx +ax +ab
= x^2 +(a+b)x + ab
すると、乗法公式のできあがり!
いっちょ上がりさ。
平方の公式の証明
つぎは平方の公式の証明だね。
こいつも分配法則で証明できちゃう。
まず、(a+b)^2をかけ算になおしてみよう。
すると、
(a+b)^2
= (a+b)(a+b)
になるね。
これをさっきみたいに分配法則で展開してみよう。
まず、いちばん左の「a」を後ろの「a」と「b」にかける。
そして、たす。
(a+b)^2
= (a+b)(a+b)
= a^2 + ab
つぎは、「b」を後ろの「a」と「b」にかける。
そして、たす。
(a+b)^2
= (a+b)(a+b)
= a^2 + ab + ab + b^2
あとは同類項をまとめるだけ。
すると、
(a+b)^2
= (a+b)(a+b)
= a^2 + ab + ab + b^2
= a^2 + 2ab + b^2
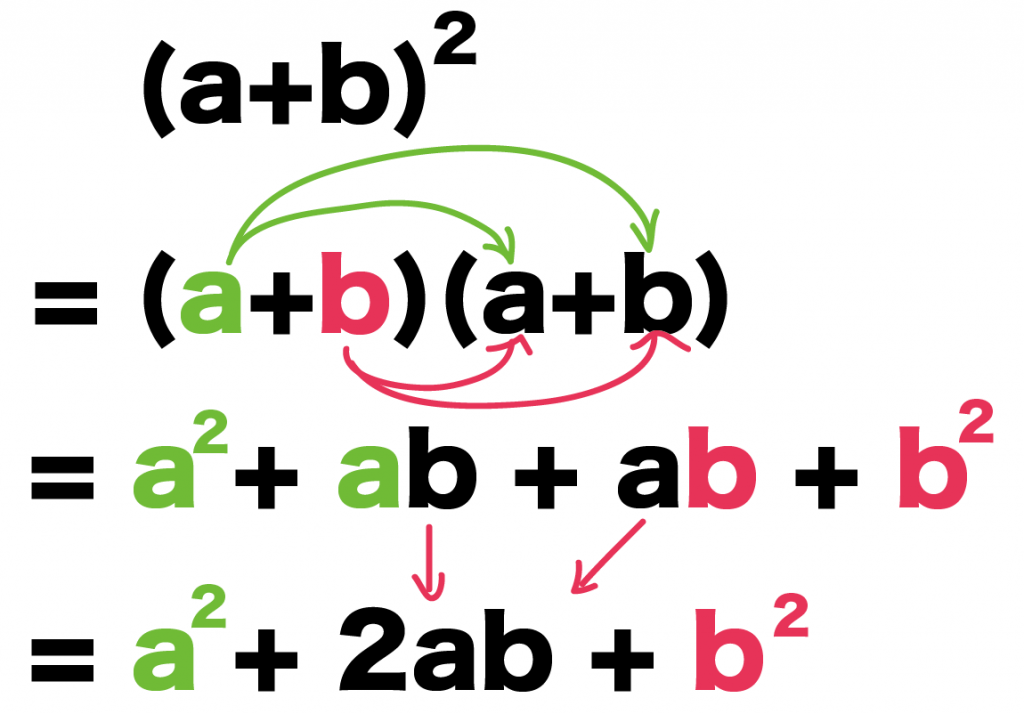
あら。
平方の公式のできあがり!
和と差の積の証明
いよいよ「和と差の積」の公式の証明だ。
こいつも分配法則で一発。
まず、いちばん左のaを右の()内の項にかける。
そして、たす。
(a +b) (a-b)
= a^2 – ab
2つめの「b」を後ろの()にかけてやると、
(a +b) (a-b)
= a^2 – ab +ab -b^2
になるね。
あとは同類項をまとめてやろう。
- -ab
- ab
の2つだね。
こいつらをたして消してやると、
ほら!
乗法の公式の「和と差の積」のできがあがり。
まとめ:乗法の公式は「分配法則」と「同類項」で攻略!
乗法公式を覚えることは大切。
だけど、
テストで忘れたら危機。危機におちいる。
だからこそ、
なぜ乗法公式がつかえるのか??
ってとこまでおさえておこう。
そんじゃねー
Ken