【中学確率】樹形図の書き方がわかる3ステップ
確率の樹形図の書き方がよくわからない??
こんにちは!この記事をかいているKenだよ。小腹がすいたね。
中学数学の確率で便利なのは、
樹形図
というアイテムだ。
樹形図とは文字通り、
樹の形みたいに枝分かれしている図のことだよ。
ちょうど下みたいな図だね↓↓
どう??樹の枝みたいでしょ??
中学生が勉強する確率では、
「樹形図」をつかって場合の数をかぞえていくんだ。
確率では樹形図がむちゃ重要ってわけ。
確率の樹形図の書き方がわかる3ステップ
さっそく樹形図をかいていこう。
3ステップでかけちゃうんだ。
- トライアル数を上にかく
- 1回目の予想される結果をかく
- 前回の結果をふまえてどうなるかかく
つぎの例題をときながら解説していくよ。
例題
3・4・8がかかれたカードを3枚ならべてできる整数の場合の数を求めなさい。
Step1. トライアル数をかく!
まずは何回挑戦できるかかいてみよう。
つまり、
トライアル数ってわけ。
コインを3回なげるんなら「3」、
くじ引きを2回ひけるなら「2」がトライアル数だね。
例題のトライアル数は「3」。
なぜなら、
カードを3枚並べられるからさ。
もちろん、カードを4枚ならべるなら「4」、
120枚並べるなら「120」がトライアル数だ。
このトライアル数をヨコにずらーっと書いてみよう!
Step2. トライアル1で予想される結果をかく!
まずは一回目のトライアルでどうなるか考えてみよう。
コインだったら表か裏か。
くじ引きだったら当たりか・はずれだね。
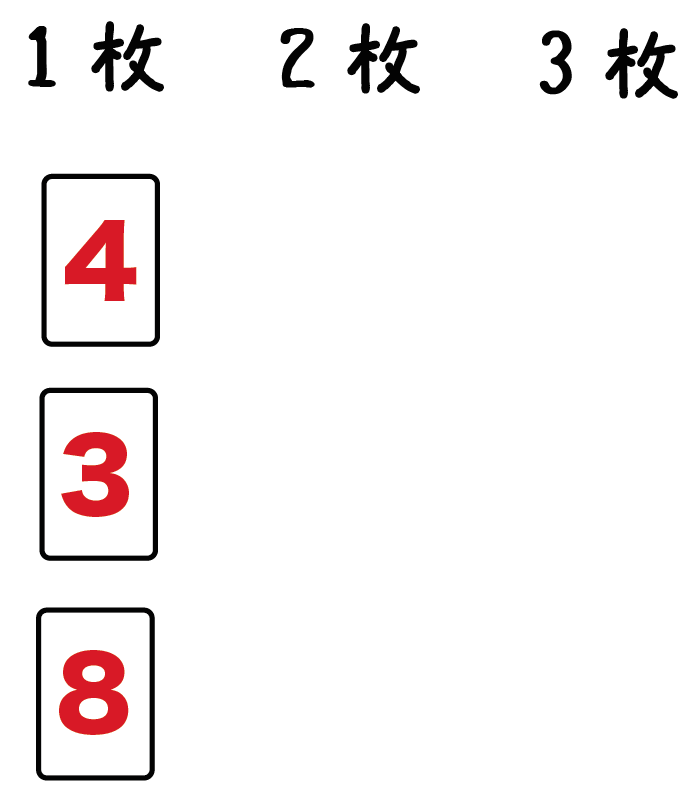
例題で1枚目になるのは、
- 3
- 4
- 8
のいずれかのカードだね??
つまり、
1枚目は3枚のどれかってわけ。
だから、「1枚」の下に「3」「4」「8」の3通りをかいてあげよう。
Step3. 前回までの結果からどうなるか考える
つぎは、前回のトライアルの結果をふまえてどうなるか??
ってことを考えてみよう。
1回目が終わったら、1回目をふまえて2回目。
2回目が終わったら、1・2回目をふまえて3回目
の結果を予想するんだ。
例題でいうと、
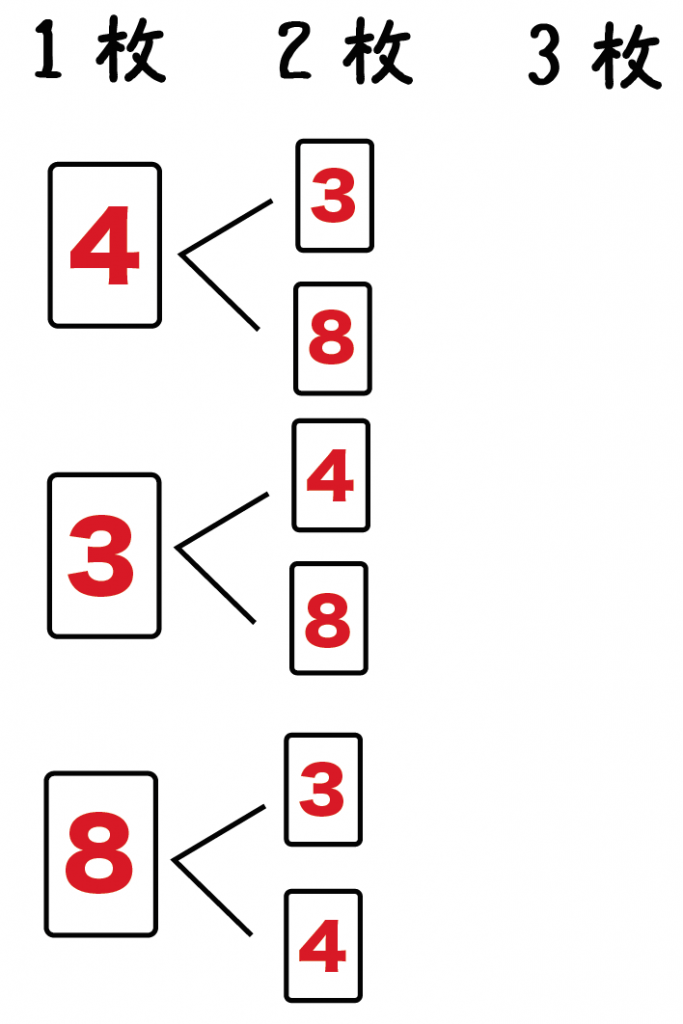
1回目のトライアルの後、残されたカードは2枚。
1枚目に4がくると、
つぎは「3」か「8」の結果になる。
おなじように「3」と「8」がきている場合を考えると、
こんな樹形図になるはず↓↓
同じように、3回目の結果も予想してみよう。
2枚カード並べたら残り1枚だね。
つまり、残っているカードを並べるだけってことだ。
だから、3枚目も加味するとこうなるはず↓↓
おめでとう!これで樹形図は完成だね。
すべてのカードの並び方は6通りってわけ!
まとめ:樹形図の書き方は前の結果をふまえろ!
樹形図の書き方はどうだったかな??
ポイントは、
前のトライアルの結果をふまえること。
これにつきるね。
1回目のトライアルが終わったら2回目はどうなるのか。
これをイメージしてみよう。
そんじゃねー
Ken