【簡単公式】3秒でわかる!四角形の内角の和の求め方
四角形の内角の和の求め方がわからんぜ??
こんにちは!この記事をかいているKenだよ。水道水、うまいね。
四角形の内角の和
ってたまに求めたいよね??
そんなときは、
多角形の内角の和の公式をつかえば一発。
n角形の内角の和は、
180× (n-2)
で計算できちゃうんだ。
四角形の内角の和は、
nに「4」を代入してやればいい。
すると、
180× ( n -2 )
= 180 × (4-2 )
= 360°
って計算できちゃう!
つまり、四角形の内角の和は、
360°
になるんだ!!!
なぜ四角形の内角の和は360°になっちゃうの??
でもさ、
なぜ四角形の内角の和は360°になるんだろう??
便利すぎてこわいよね。。
せっかくだから、
内角の和が360°になる理由をさぐっていこう。
その理由はずばり、
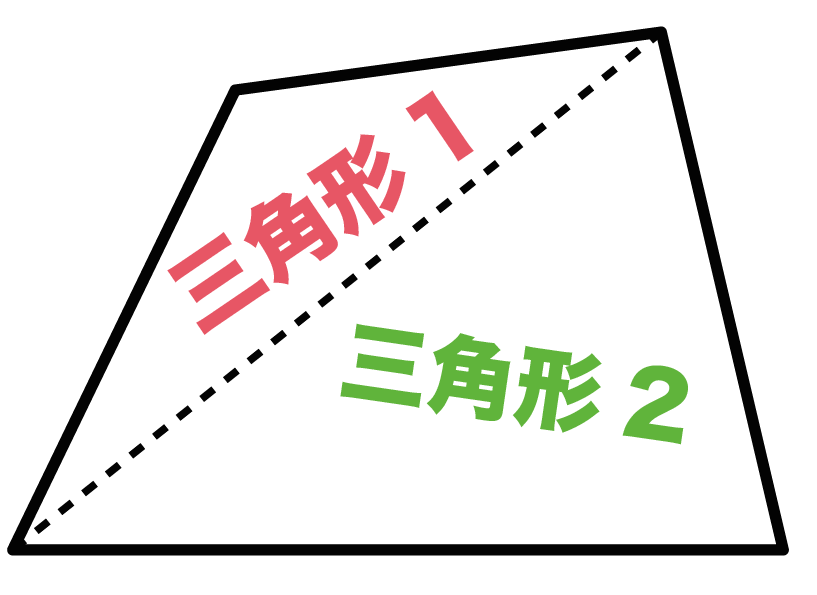
四角形に「三角形が2つ」含まれているからなんだ。
対角線をすーーーっとひいてみよう。
すると、
そこには、
三角形が2つ出現しているはず。
んで、
三角形の内角の和は180°だったよね??
ってことは、
三角形が2つ隠れている四角形の内角の和は、
180°×2
= 360°
になるってわけ。
これで四角形の内角の和を計算できたね。
まとめ:四角形の内角の和は360°である!
多角形の内角の和を求めたいときは、
三角形が何個かくれているのか??
を調べてみよう!
そんじゃねー
Ken