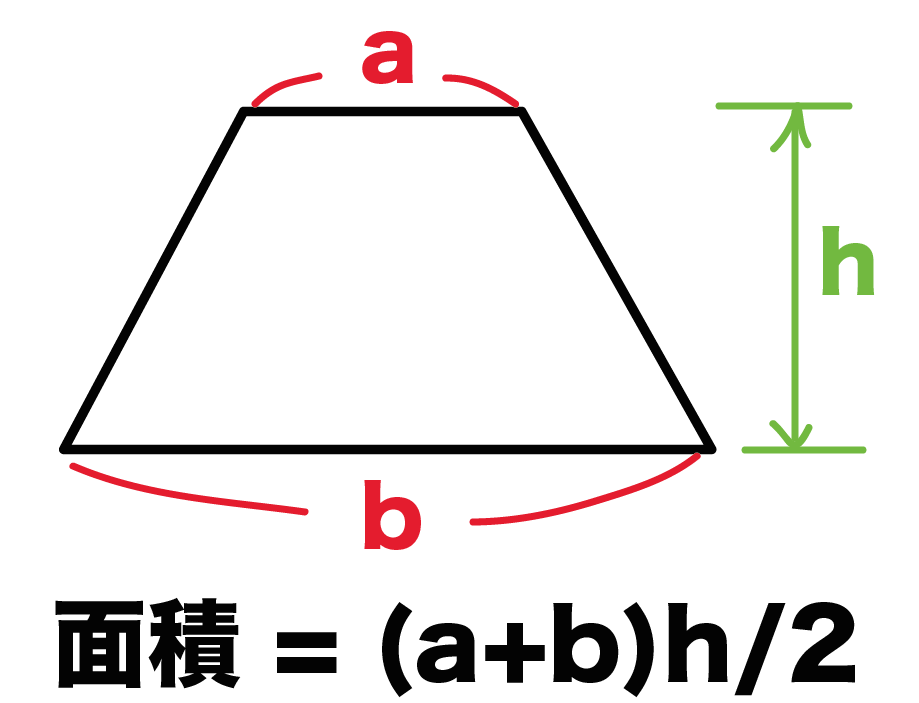
台形の体積の公式の求め方を知りたい！？
こんにちは！この記事をかいているKenだよ。着る毛布ほしいね。
台形の体積の求め方を教えてほしい。
そう、きかれることが結構ある。
正直ドヤ顔で、
台形の体積はね・・・
って答えそうになる。
だけれども、
そもそも台形に体積はないんだ！
台形は平面図形だからね。
台形の面積なら求められるけど、体積は無理なんだ。
でもさ、いったい、、
台形の体積ってなんだろう？？
たぶん、みんながいってる「台形の体積」は、
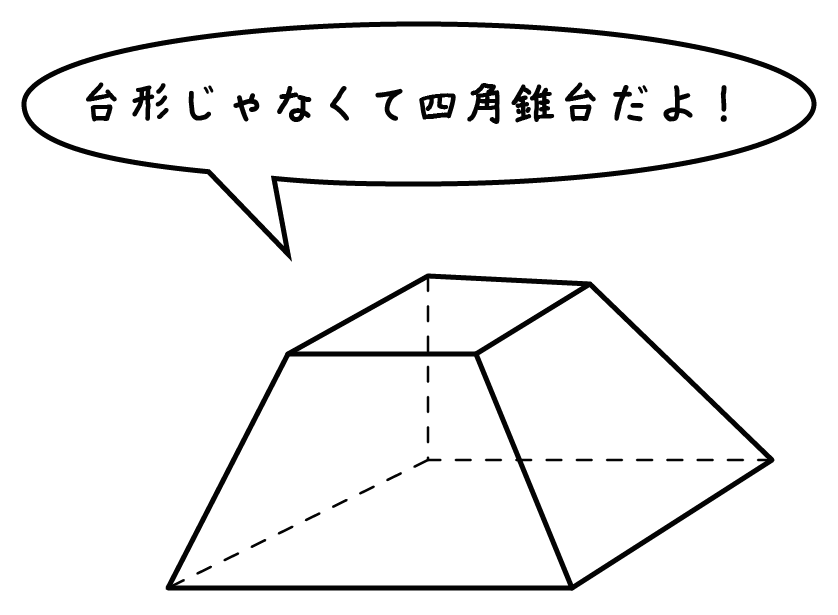
正四角錐台の体積
のことなんじゃないかな。
プリンみたいな立体だよ。
正四角錐台は台形の立体バージョンにみえるし、たぶんそう。。
そこで今日は台形の体積のかわりに、
正四角錐台の体積の求め方の公式を紹介するよ。
よかったら参考にしてみて。
台形の体積（正四角錐台）の求め方の公式！？
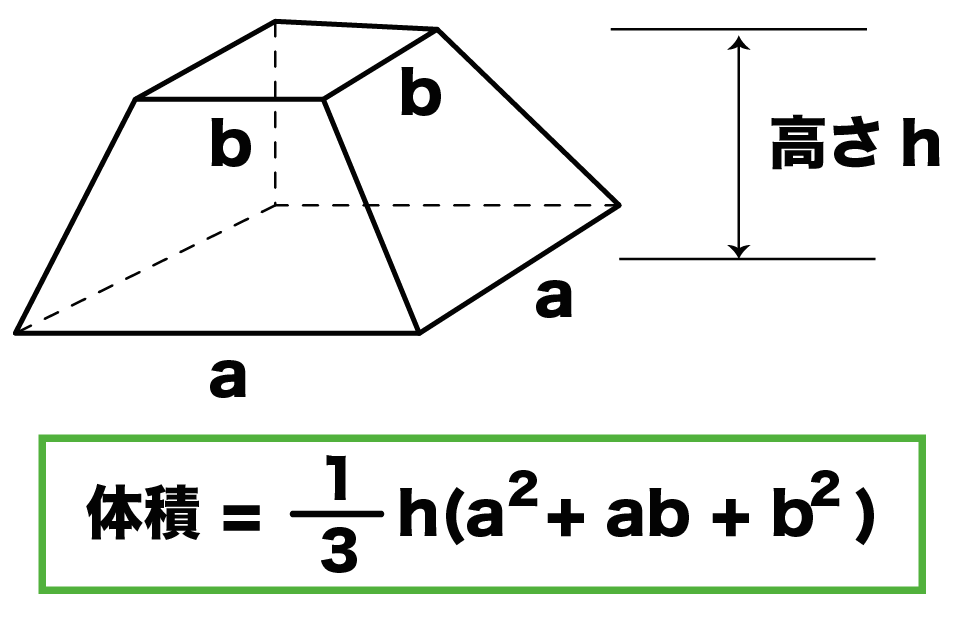
正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。
体積は、
1/3 h ( a^2 + ab + b^2)
で計算できちゃうんだ。
つまり、
{（下の辺）×（下の辺）+ （下の辺）×（上の辺）+ (上の辺) × (上の辺) }×高さ÷3
ってことさ。
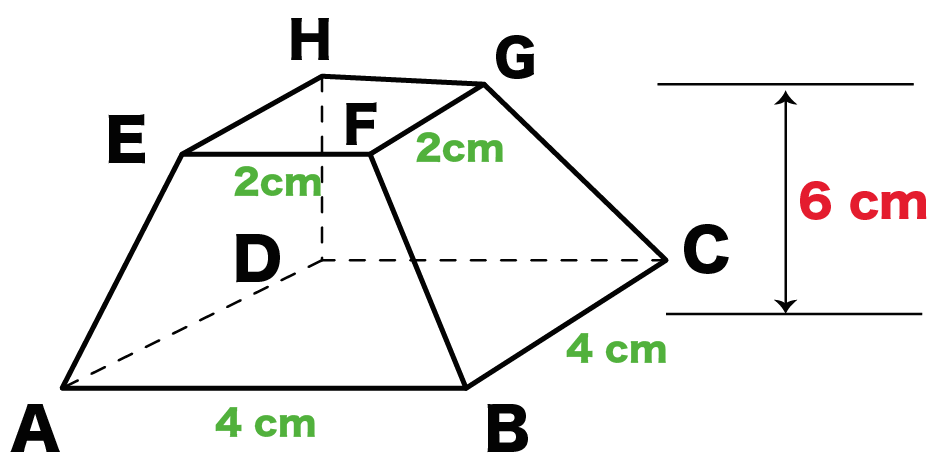
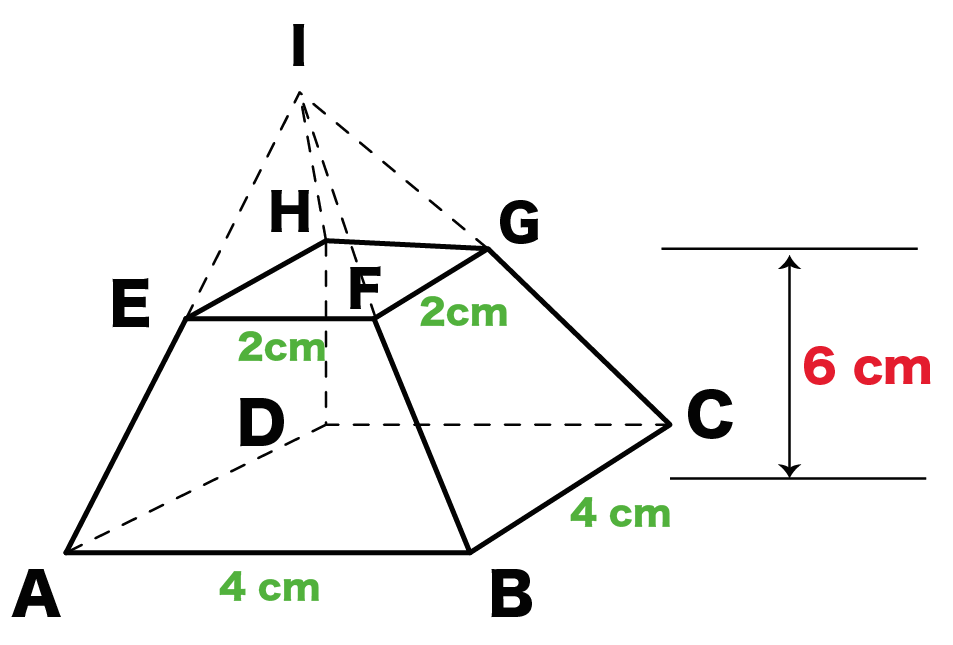
たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。
この立体の体積は、
1/3 h ( a^2 + ab + b^2 )
= 1/3 × 6 × ( 4^2 + 4 × 2 + 2^2)
= 2 × ( 16 + 8 + 4 )
= 56 [cm^3]
になるよ！
めんどい計算式だけど、
落ち着いて計算してみよう！
台形の体積の公式がわかる3ステップ
むちゃ便利だけど、
なんで公式で計算できちゃうんだろう？？
ちょっと怪しい。
今日はそんな流れで、
台形の体積（正四角錐）の求め方をみちびいてみよう！
3ステップでできちゃうよ。
Step1. みえない四角錐をかく！
まず、みえてない四角錐をかこう。
正四角錐台の斜辺を延長すればいいんだ。
正四角錐台ABCDEFGHでいうと、
- AE
- BF
- CG
- DH
の4辺を延長してあげるんだ。
そんで、その交点をIとするよ。
これでみえなかった「正四角錐EFGHI」があらわれたね。
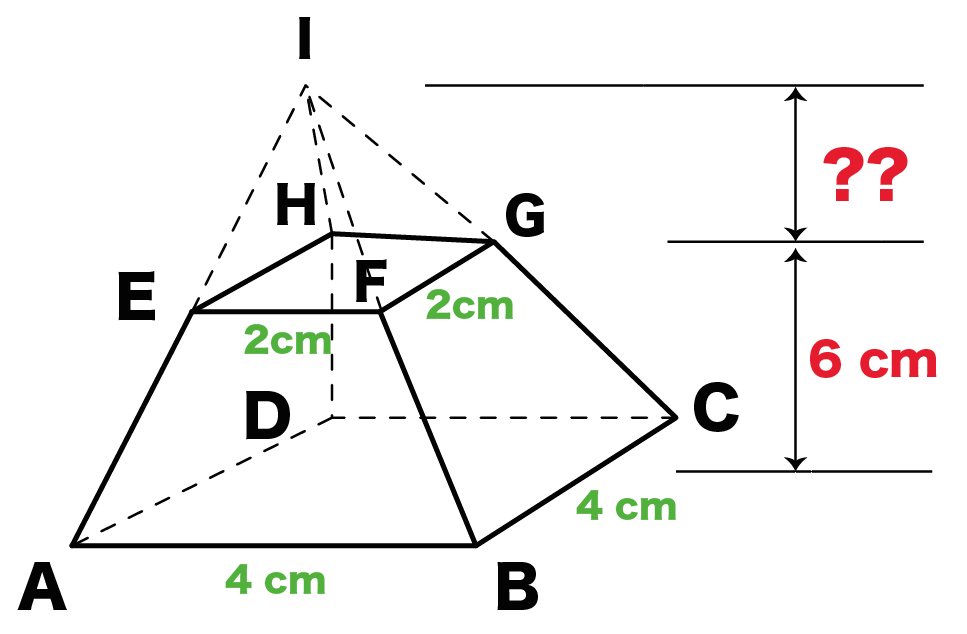
Step2. 高さを求める！
みえない正四角錐の高さを求めよう。
例でいうと、
正四角錐 I-EFGHの高さだね。
FG：BC = 2：4 だから、
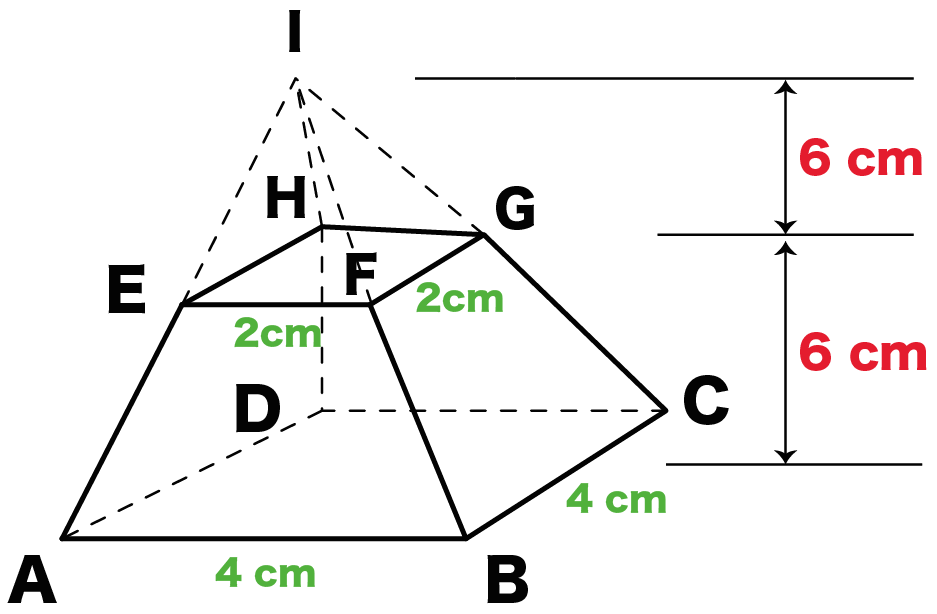
（正四角錐I-EFGHの高さ）：（正四角錐I-ABCDの高さ）= 2：4
（正四角錐I-EFGHの高さ）：（正四角錐I-EFGHの高さ） + 6 = 2：4
（正四角錐I-EFGHの高さ）= 6
になるね！
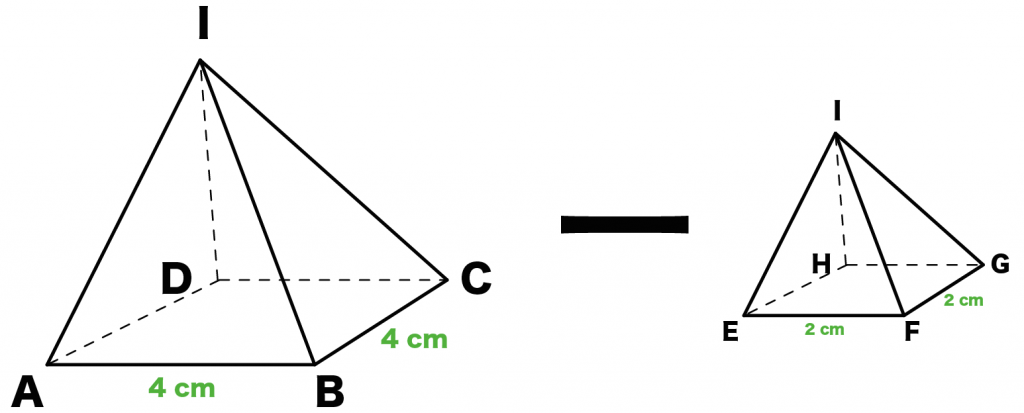
Step3. 「大きい四角錐」から「小さい四角錐」をひく！
最後は、「大きい四角錐」から「小さい四角錐」をひこう。
そうすれば「正四角錐台」の体積になる。
さっきの例でいうと、
「正四角錐I-ABCD」から「正四角錐I-EFGH」をひけばいいんだ。
地道に計算してやると、
（正四角錐I-ABCD）- （正四角錐I-EFGH）
= 1/3 × ( 6+6) × 4^2 – 1/3 ×6 × 2^2
= 64 – 8
= 56[cm^3]
になる。
おめでとう！
これで台形の体積、、じゃなくて、
正四角錐台の体積を計算できたね！！
まとめ：台形の体積の求め方は「上 – 下」！！
台形の体積（正四角錐台）の体積の求め方はどうたった？？
大きな正四角錐から小さいやつをひけばいいんだ。
補助線をひいて正四角錐をみつけてみよう。
そんじゃねー
Ken
