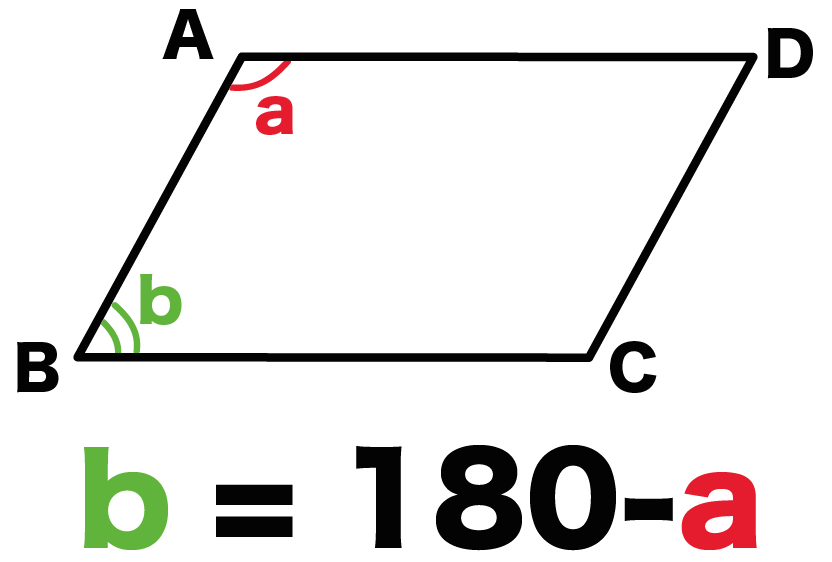平行四辺形の角度の求め方がわからん？？
こんにちは！この記事をかいているKenだよ。リフティング、はじめたよ。
平行四辺形の角度を求める公式ってしってる？？
角度をa、その隣の角度をbとすると、
b = 180 -a
になるんだ！
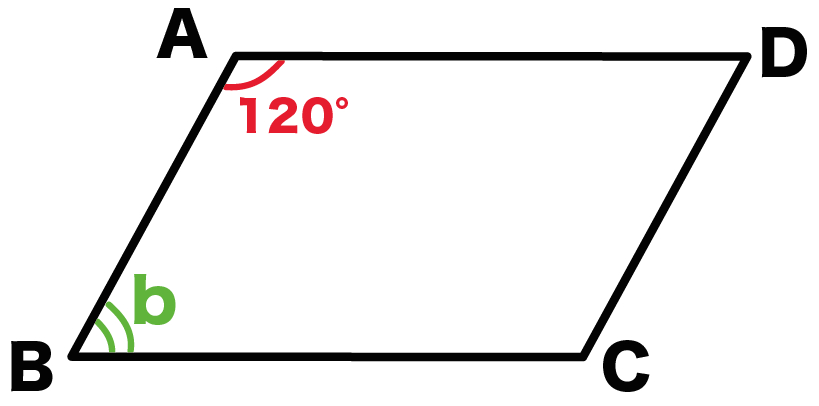
たとえば、角A = 120°の平行四辺形ABCDがあったとしよう。
このとき公式をつかうと、
角B = 180 -120
= 60°
になるんだ！
どう？？ むちゃ便利な公式でしょ！？？
平行四辺形の角度の求め方がわかる3ステップ
今日はせっかくだから、
なぜ公式で平行四辺形の角度が求められるのか？？？
ってことを振り返ってみよう。
さっきの「平行四辺形ABCD」をつかうよ。
公式なしで、角Bを計算していこう！
Step1. 向かいあう角をだす！
まずは向かいあった角を計算してやろう。
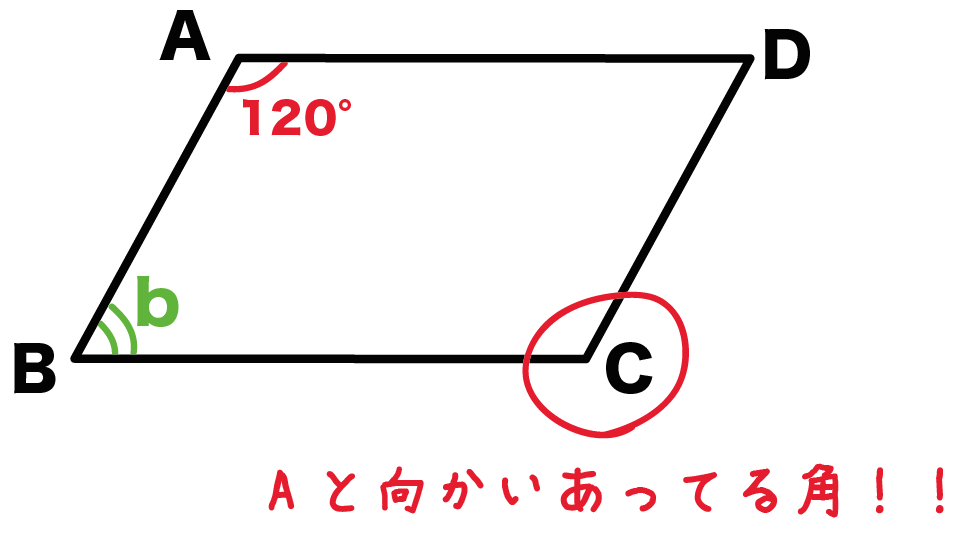
平行四辺形ABCDでいうと、角Aの角度がわかってるね？？
ってことは、
向かいあっているのは「角C」だ。
「2組の向かいあう角の大きさはそれぞれ等しい」
という平行四辺形の性質をつかってあげよう。
すると、
角C = 角A = 120°
になるはずだ！
これが第一ステップ！
Step2. 残りの内角の和を計算！
平行四辺形の2つの角度がわかったね。
つぎは、
残り2つの角度をたしたらいくつになる？？
ってことを計算するよ。
四角形の内角の和は、
360°
だったよね？？
この「360°」から2つの角度をひけばいいんだ。
平行四辺形ABCDでいうと、
「角A」と 「角C」が120°ってことがわかった。
つまり、こいつらを足すと、
240°になるはずだ。
これを四角形の内角の和360°からひいてやると、
360 – 240
= 120°
になるね。
つまり、
残りの「角BとC」をたしたら120°になる
ってわけさ。
Step3. 残りの角の和を2でわる！
最後は「残りの角の和」を2でわろう。
なぜ2でわるのかというと、
残り2つの角度も等しいからだよ。
だって、平行四辺形の性質の、
「向かいあう角が等しい」
ってやつが使えるからね。
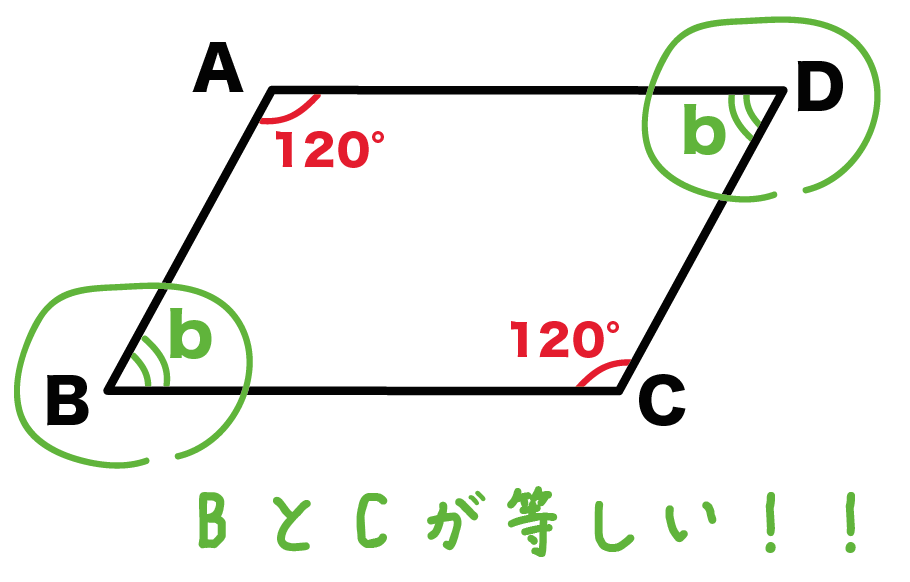
平行四辺形ABCDでいうと、BとDが等しいってことなんだ。
角Bと角Dをたしたら120°になる。
しかも、角B =角Dだから、
角B + 角D = 120
角B + 角B = 120
角B = 角D = 60°
になるね。
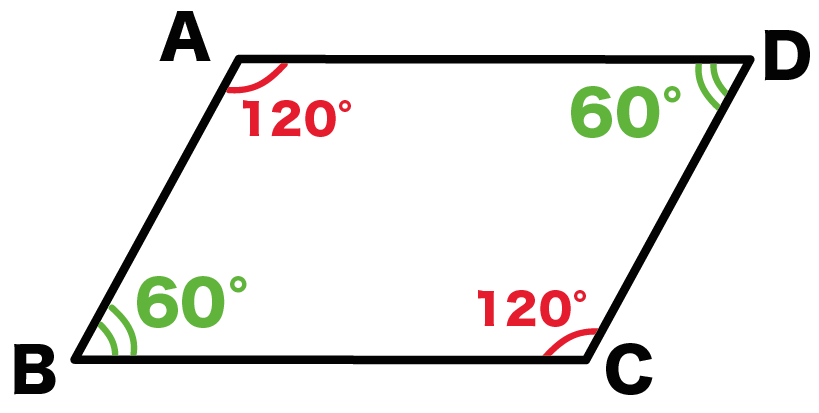
おめでとう！
平行四辺形の角度を求められたね！
まとめ：平行四辺形の角度の求め方は「性質」を使い倒せ！
平行四辺形の角度の求め方はシンプル。
180°から「隣の角の大きさ」をひけばいいんだ。
便利な公式だけど、
なぜ公式がつかえるのか？？
ってことをおさえておこう。
そんじゃねー
Ken
