3分でわかる!平行四辺形の定義とは??
平行四辺形の定義ってなによ??
こんにちは!この記事をかいているKenだよ。腹巻きは、神だね。
平行四辺形ってなんだろう??
響きはかっこいいし、
形も悪くない。
でも、正直、
よくわかっていないのが現実だ。
そこで今日は、
平行四辺形の定義をわかりやすく解説していくよ。
よかったら参考にしてみて。
3分でわかる!平行四辺形の定義
平行四辺形の定義は、ずばり、
2組の向かいあう辺が、それぞれ平行な四角形
だ。
たとえば、
平行四辺形ABCDがいたとしよう。
このとき、
向かい合う辺である、
- AB とCD
- ADとBC
たちはそれぞれ平行になってるんだ。
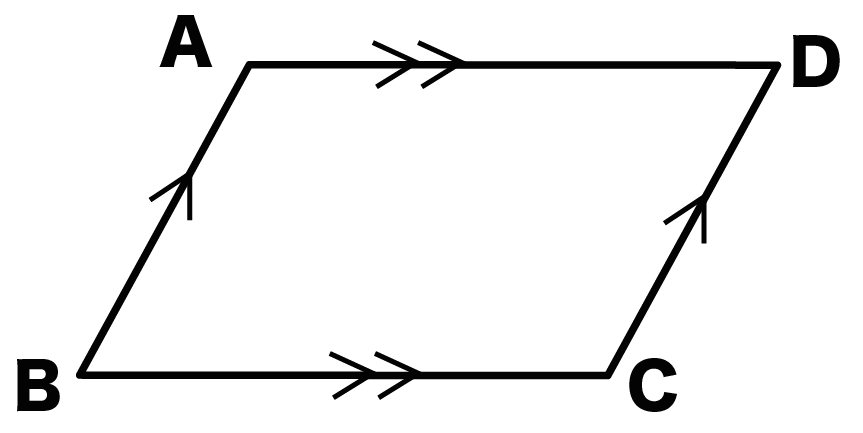
つまり、
- AB// CD
- AD // BC
ってわけだね。
えっ。
ぴんとこないって??
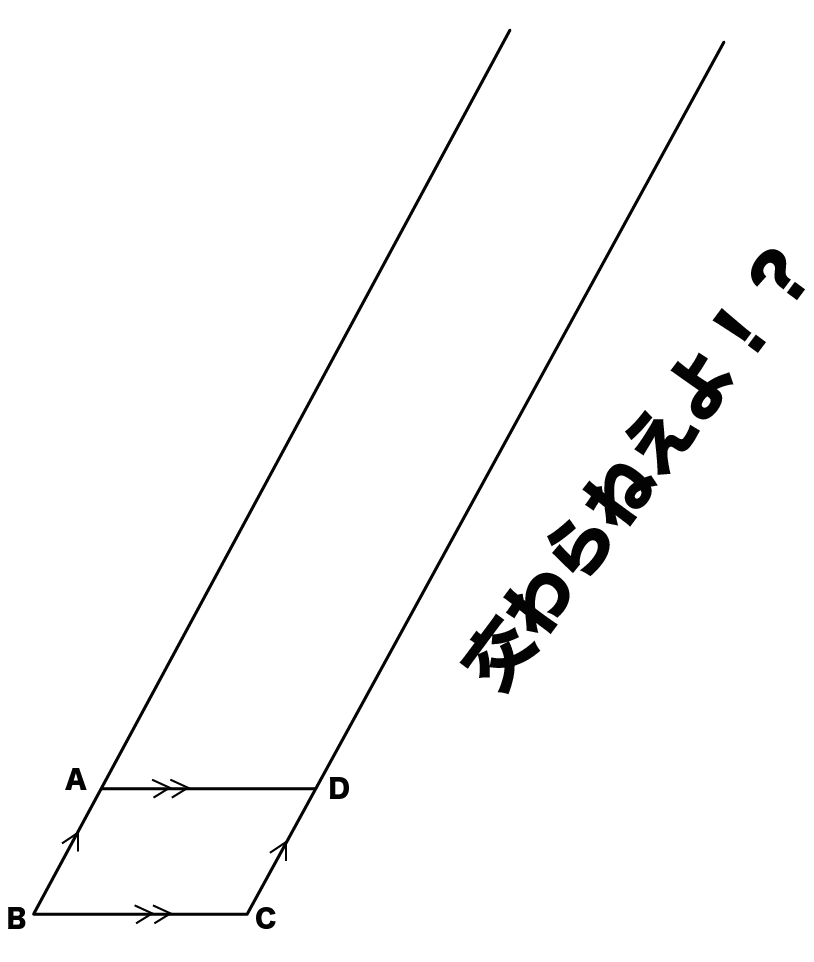
そうだなあ、ようするに、
ABとCDをのばしまくっても交わらないし、
ADとBCをのばしまくっても交わらないんだ。
こんな感じで、
2組の向かいあう辺が、それぞれ平行な四角形
が平行四辺形なのさ。
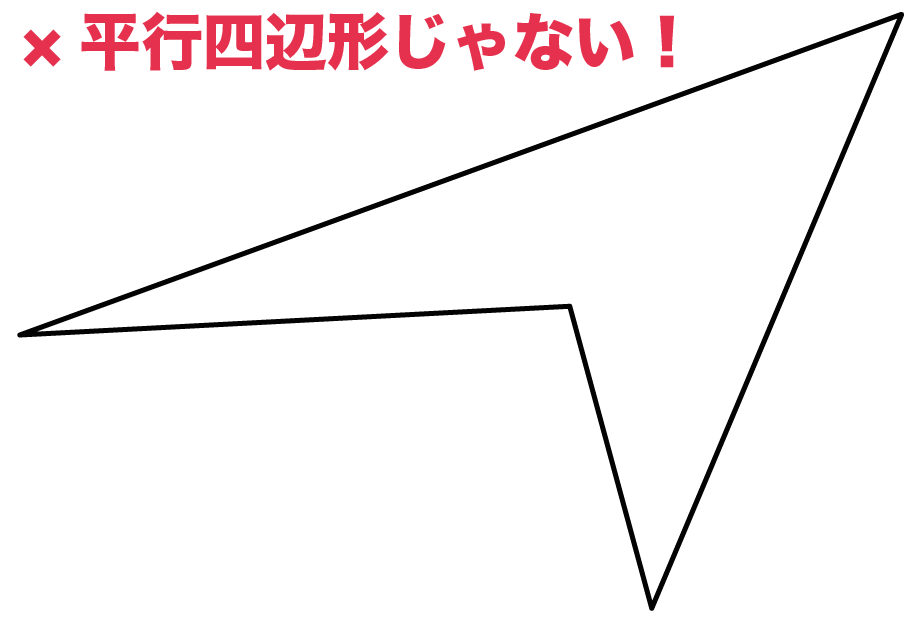
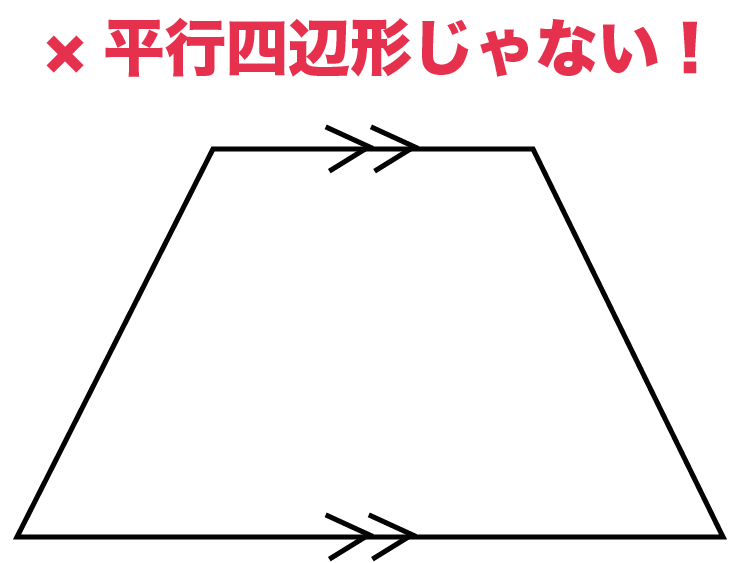
こいつらは平行四辺形じゃない!??
だから、
「辺が平行ではない四角形」は平行四辺じゃない。。
1組の辺だけ平行でもダメ。
そいつは、平行四辺形じゃない。
ただの台形だ。
2組の辺が平行でも、
そいつが「六角形」だったら意味がない。
ちょっと変わった六角形さ。
平行四辺形なんかじゃああない。
こんなやつらじゃなくて、
2組の向かいあう辺が、それぞれ平行な四角形
が平行四辺形だってことをおぼえておこう!

まとめ:平行四辺形の定義は平行になっている組数がカギ
平行四辺形の定義はシンプル。
2組の向かいあう辺が、それぞれ平行な四角形
が定義なんだ。
まずは定義をがっつりおさえよう!
そんじゃねー
Ken