対頂角の問題の解き方がわからん！
こんにちは！この記事をかいてるKenだよ。ラーメンは2日に一回でいいね。
対頂角の性質は、
「対頂角は等しい」ってやつだったね。
コイツはむちゃくちゃ便利なんだ。
たとえば、
2直線でできている角度a・bがあったとする。
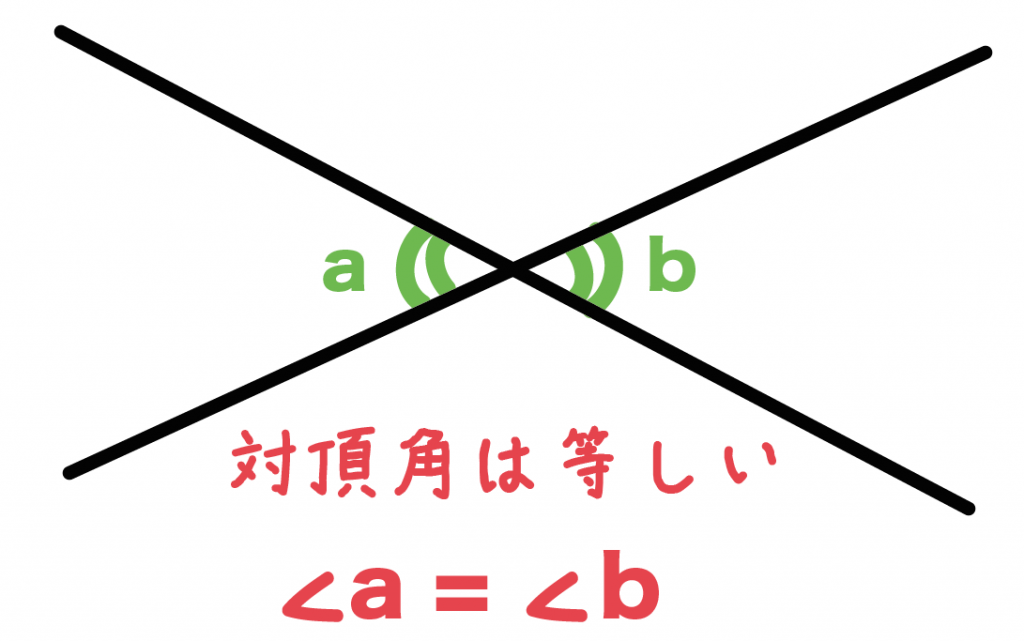
このとき、対頂角のaとbは等しいってわけさ。
今日は、
コイツでガンガン問題をといていこう！
対頂角の性質をつかって問題を瞬殺する方法
つぎの問題をといてみよう。
例題
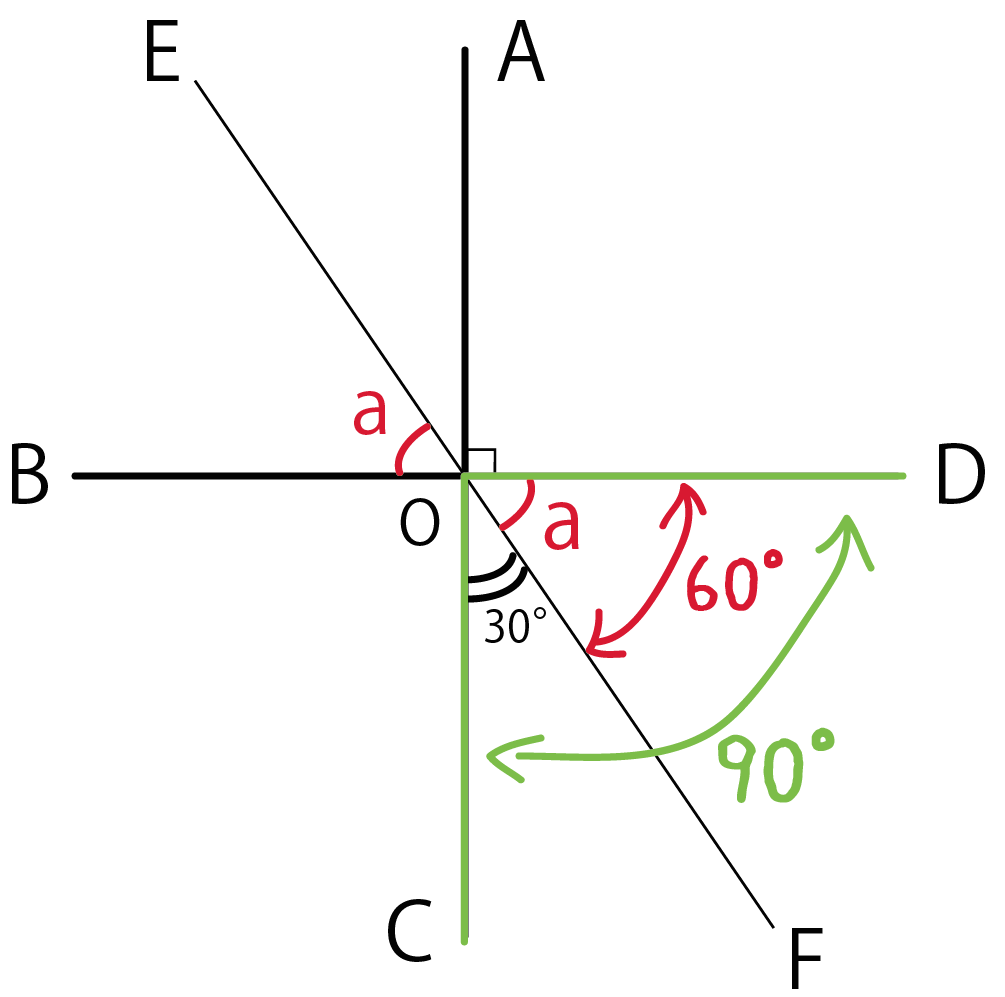
下の図のように3直線が1点で交わっています。このとき、角度aの大きさを求めなさい。
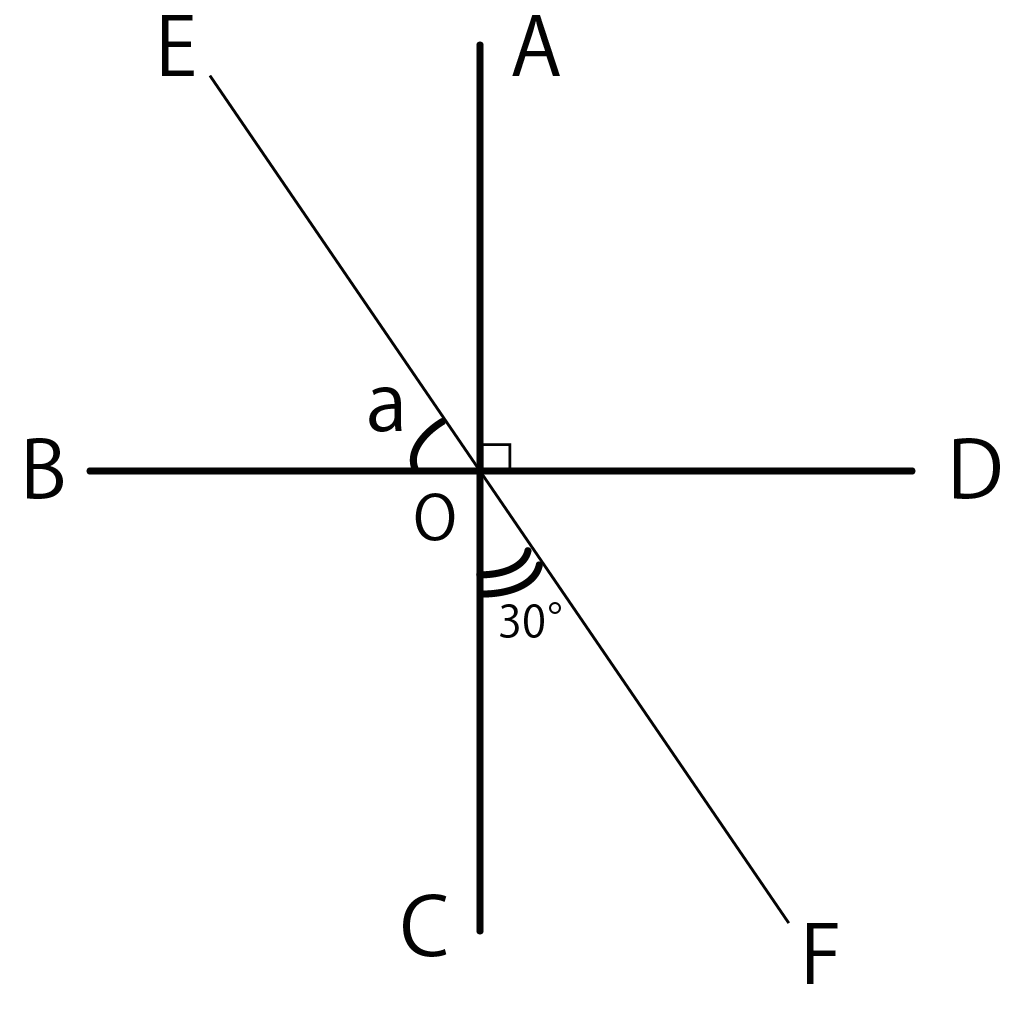
こいつは3ステップでイチコロさ。
Step1. 対頂角の性質を使う
さっそくだけど、
対頂角は等しい
という性質をつかっていくよ。
例題で、
「角BOE」と対頂角の関係にあるのは「角DOF」だね？？
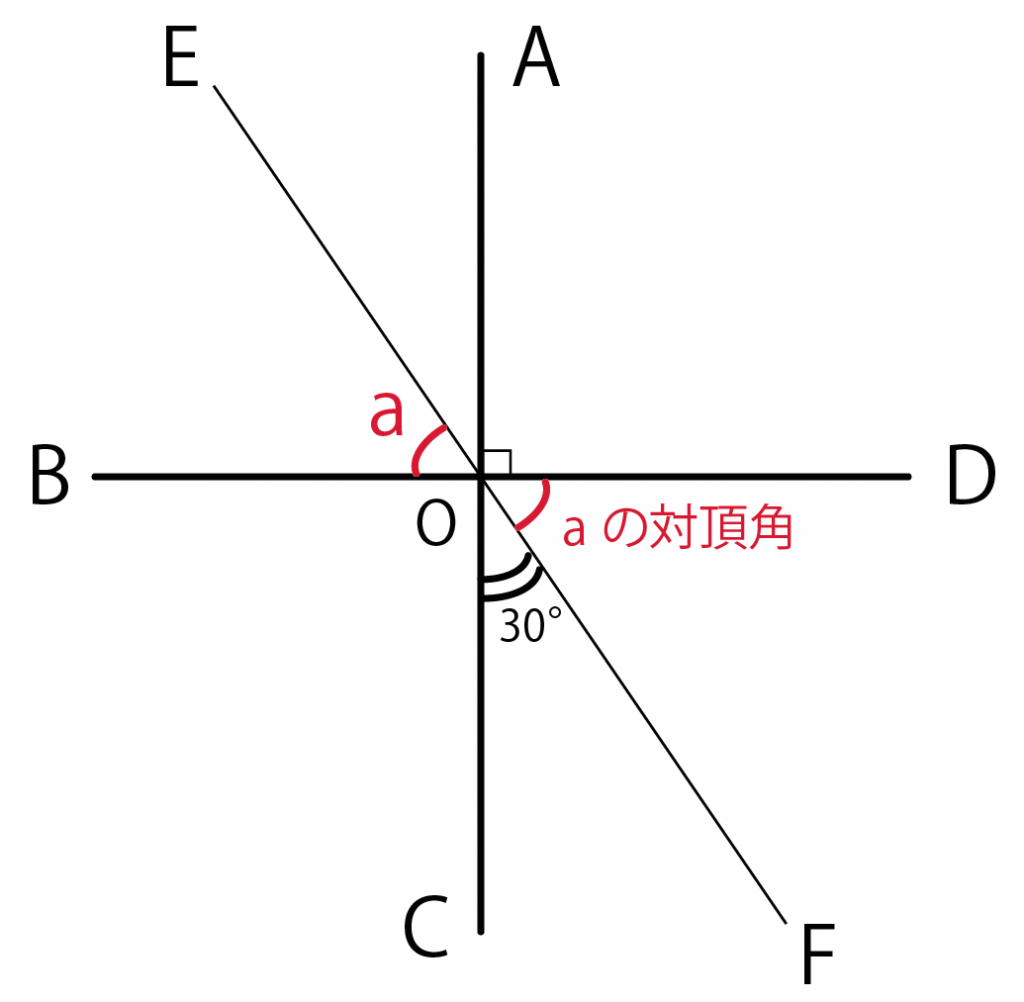
ってことは対頂角の性質をつかうと、
角BOE ＝ 角DOF ＝ a
になる。
対頂角の性質、ナイス。
Step2. 角度の等式をたてる
角度で等式をたててみよう！
例題では、
線分ACとBDは垂直に交わってるから、
角CODは90°。
よーくみてみると、
角COFと角DOF（aの対頂角）を足して90°になってるね。
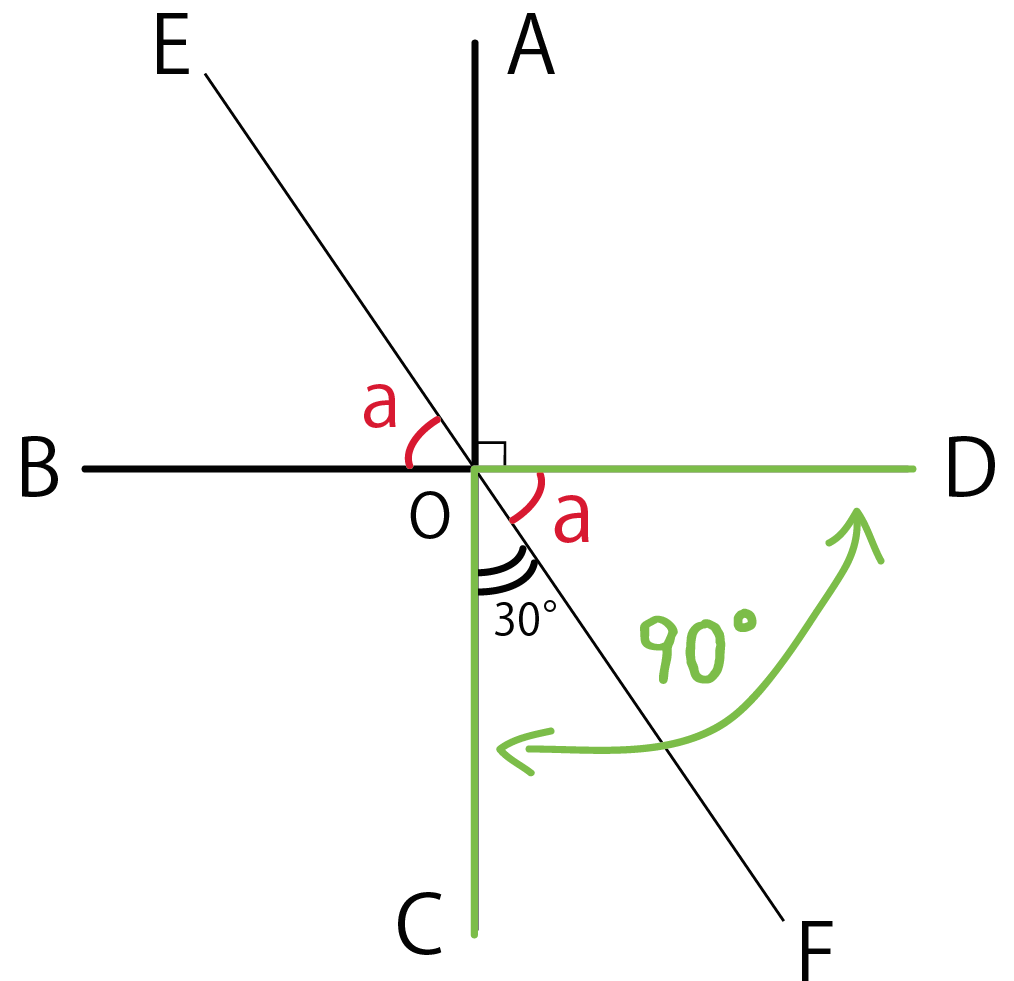
これを式になおしてやると、
角COF ＋ 角DOF ＝ 90°
という等式ができる。
角COF ＝ 30°、 角DOF ＝ a だから、
30° + a = 90°
になるね！
Step3. 等式をとく
あとは等式を根性でとくだけ。
さっきの、
30° ＋ a° ＝ 90°
をaについてとくと、
a ＝ 60°
になるよ！
つまり、
対頂角の性質をつかうと角DOF = aで、こいつに角COF（30°）をたすと、
90°の直角になるから、aは60°になるよ！
ってことさ。
どう？スッキリした？？
まとめ：対頂角の性質はもったいぶるな！！
対頂角は便利でシンプル。
だからこそ、
もったいぶらないでじゃんじゃん使っていこう。
そんじゃねー
Ken
