【一次関数の利用】動点の問題の解き方がわかる3ステップ
一次関数の利用で動点の問題がむずい??
こんにちは!この記事をかいているKenだよ。
一次関数の利用の問題ってムズい。
中でも、
動点の問題
が一番ヤッカイなんだ。たとえば、つぎのような問題だね。
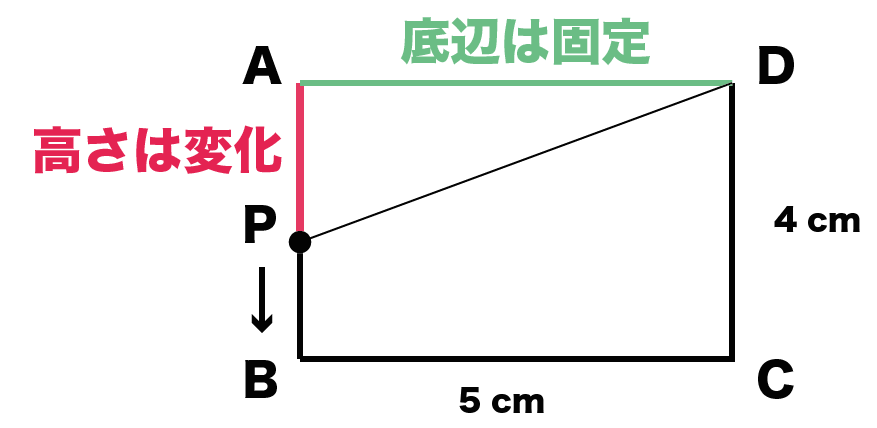
タテの長さが4cm、横の長さが5cmの長方形ABCDの周上を、点Pは毎秒1cmの速さで、AからB、Cを通ってDまで移動します。
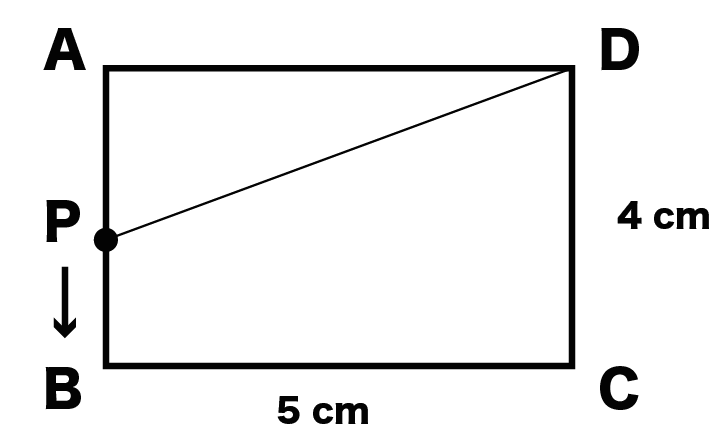
PがAを出発してからx秒後の△APDの面積をy cm²とするとき、yはxの変化にともなってどう変化するのか説明しなさい。
今日はこの動点の問題をわかりやすく解説していくよ。
よかったら参考にしてみてね。
一次関数の利用の「動点」問題がわかる3つのステップ
問題のポイントは、
三角形の高さだけが変化していること
だ。
逆に、底辺はどんなに時が経っても動かない。
高さの変化をトラッキングすれば面積が計算できそうだね。
例題でいうと、
△APDの底辺ADは固定だね?
だって、AとDは動かないからさ。
Pの移動によって高さだけ変わっていくんだ。
しかも、高さの変化は点が辺を移動するたびに変わっていくよ。
例題でいうと、動点Pが、
- 辺AB
- 辺BC
- 辺CD
にそれぞれあるときの3パターンだね。
今日はこの3つのフェーズごとに解説していくよ。
フェーズ1. 点Pが辺AB上を動いているとき
PがAB上を動いている場合だ。
このとき、△APDの高さは、
APの長さ
だよね??
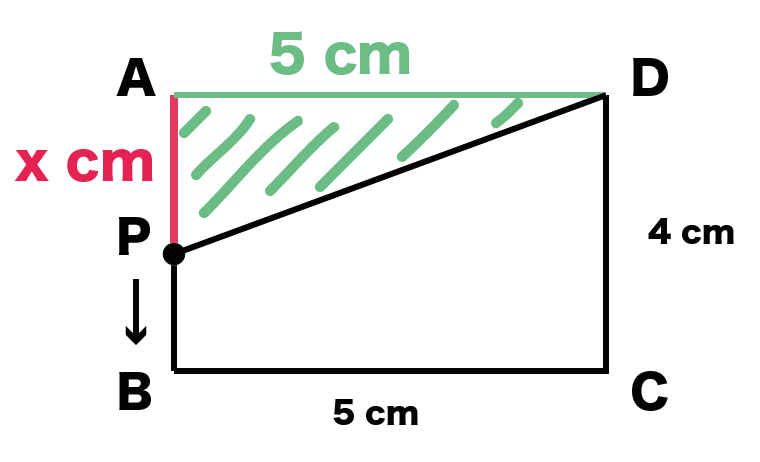
Pは1秒間にx cm動く。
APの長さはx秒後に「x cm」になっているはずだ。
よって、動点Pが辺AB上にあるとき(0 ≦ x ≦4)のとき、
△APDの面積は、
△APD = 底辺 × 高さ × 1/2
= 5 × x × 1/2
= 5/2 x
になるね。
ここまでの△APDの面積yの変化をグラフにしてみると、
こんな感じになる ↓↓
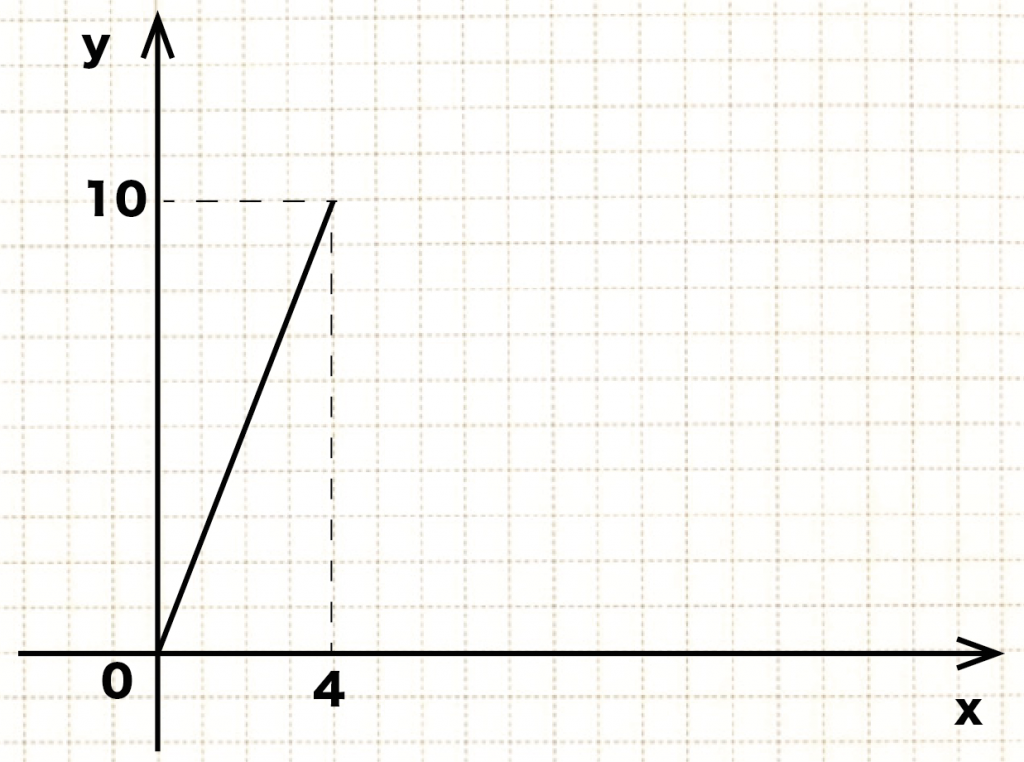
パターン2. 動点Pが辺BC上にある場合
つぎは点Pが辺BCにたどり着いたケース。
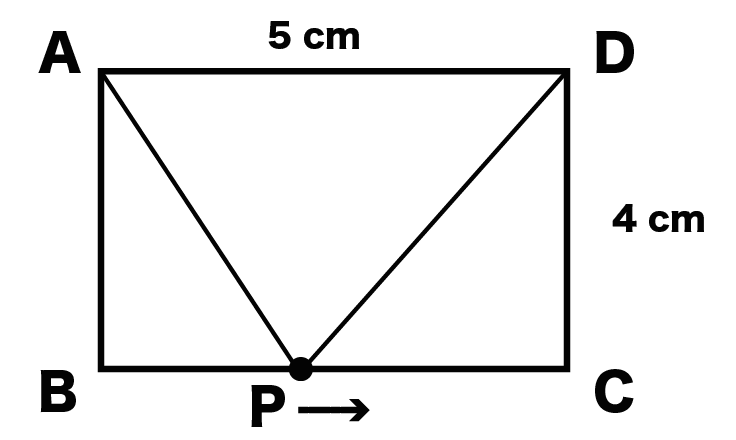
まだまだ動点Pの旅は続くんだ。辛いね。
PがBC上にあるときの△APDの高さって、
点Pから辺ADにおろした垂線になるよね?
垂線とADの交点をHとすればPHが高さってことだ。
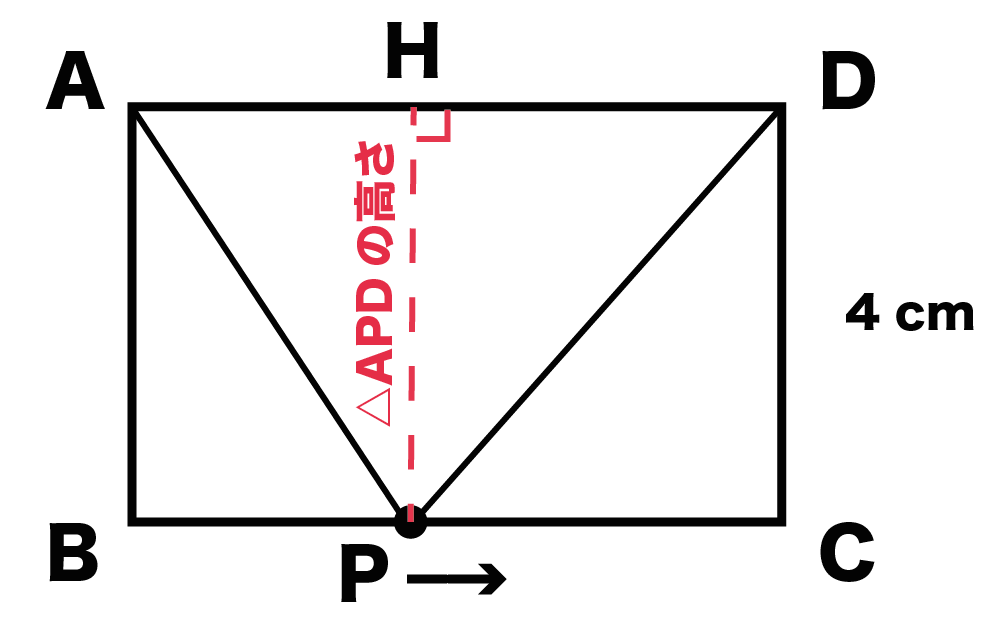
じつはこの高さって、
動点Pが左らへんにいても、
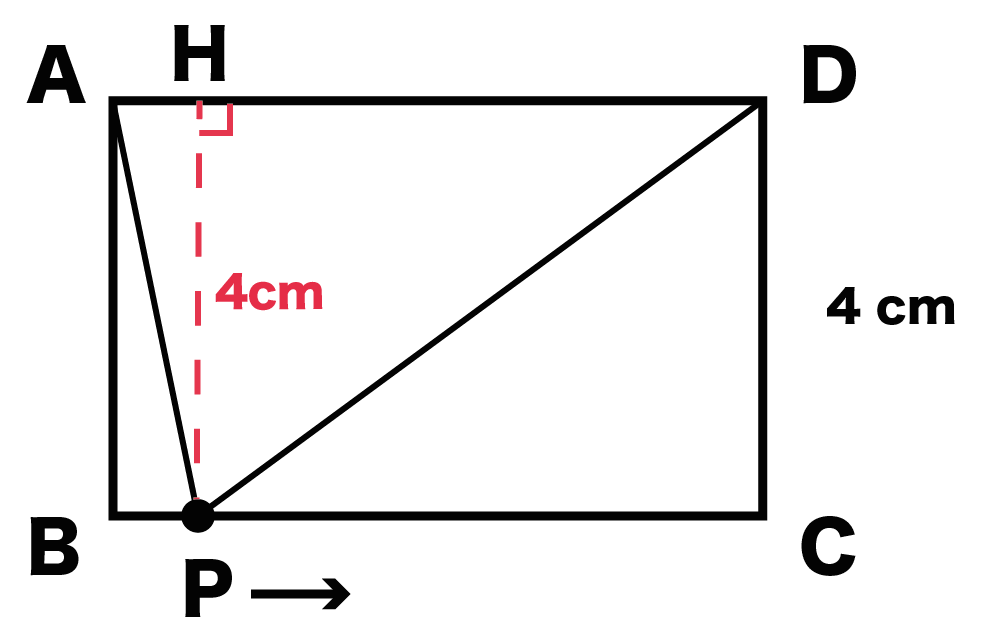
真ん中らへんにいても、
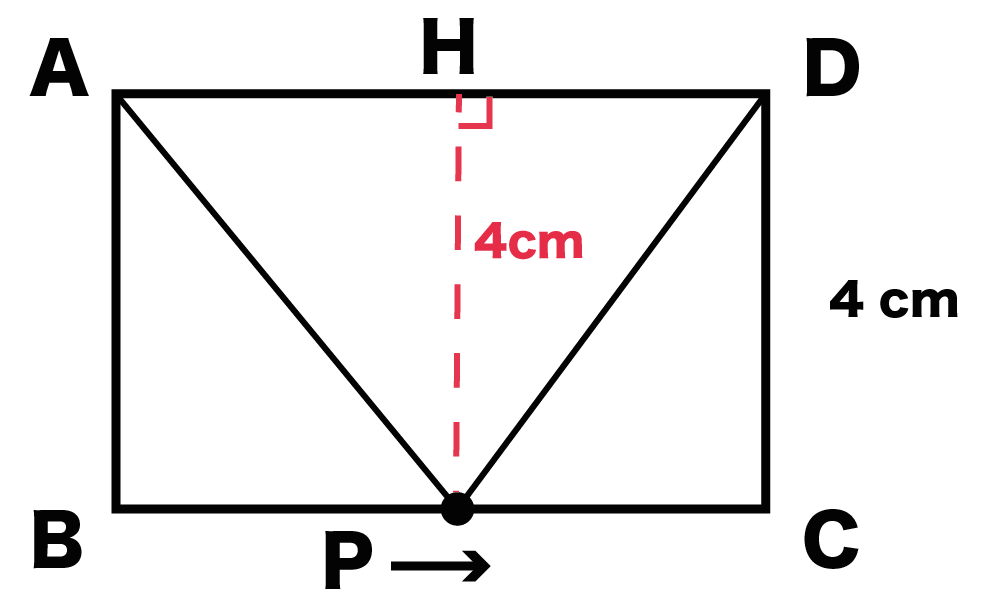
右のほうにいても、
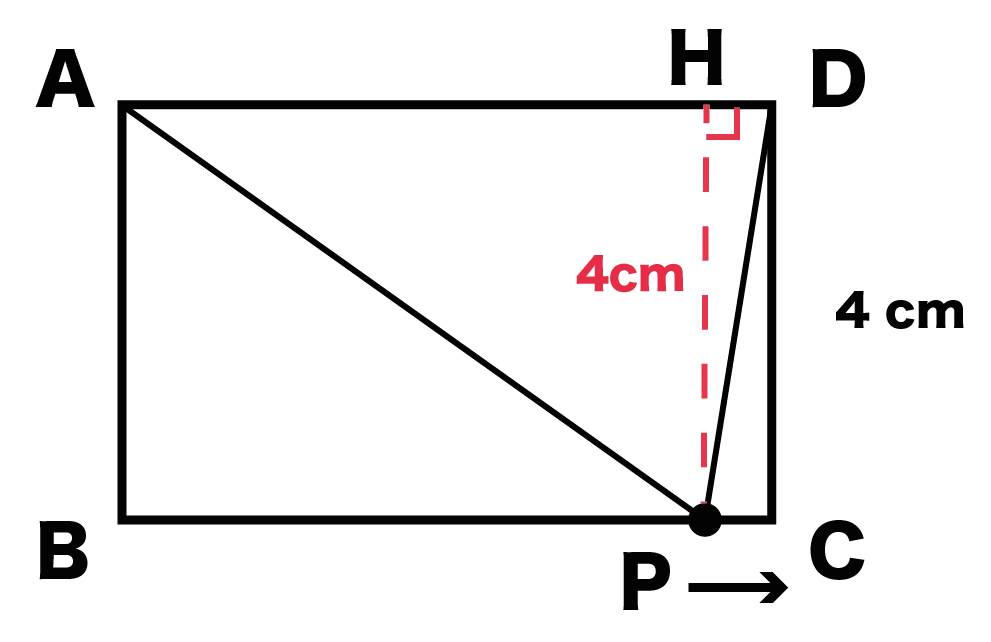
変わらないんだ!
ぜんぶ辺AB・DCと同じ長さ(4cm)になるはず。
よって、動点Pが辺BC上にあるとき(4 ≦ x ≦ 9)、
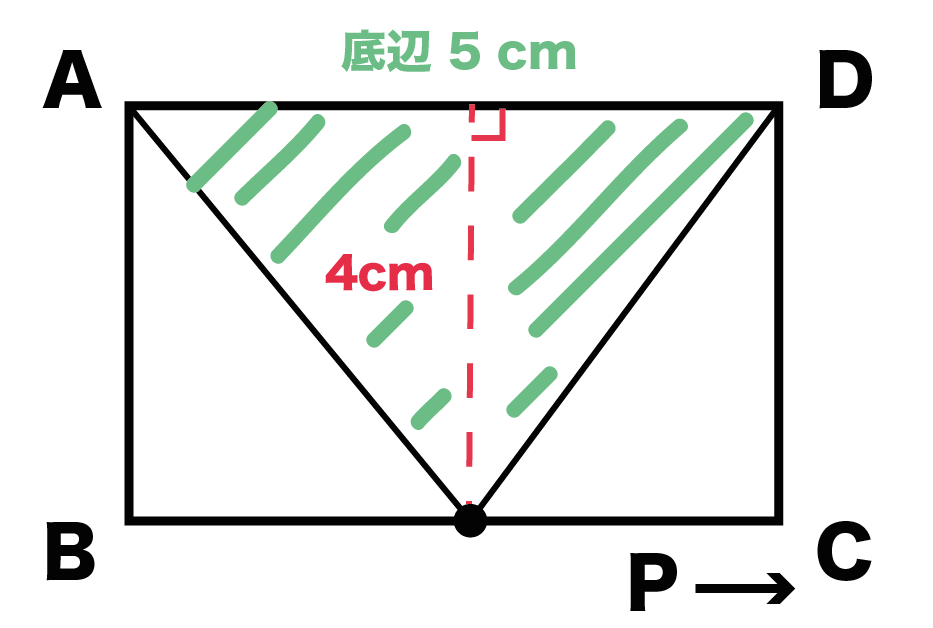
△APD の面積 = 底辺AD × 高さ × 1/2
= 5 × 4 × 1/2
= 10[cm²]
になるね。
つまり、動点PがBC上にあるとき、
△APDの面積はつねに一定というわけさ。
変数xがはいっていないからね。
ここまで△APDの面積の変化をグラフにあらわすと、
こうなるね↓↓
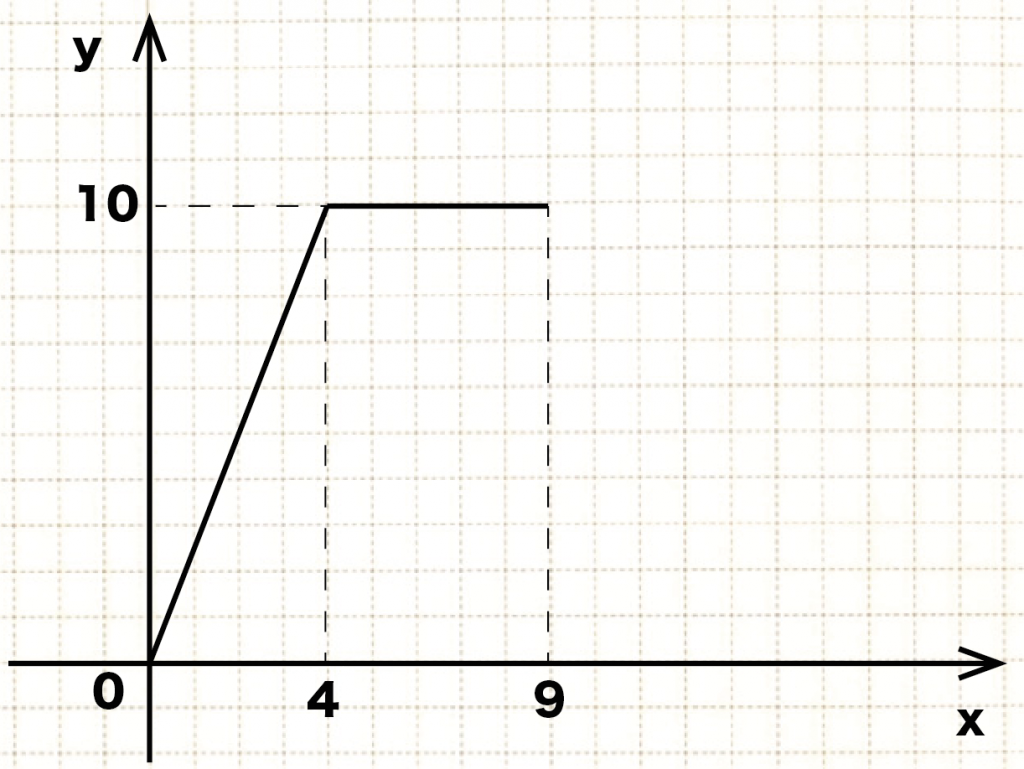
フェーズ3. 動点Pが辺CDにある場合
いよいよ最後のフェーズ。
Pが辺CDにさしかかった場合さ。
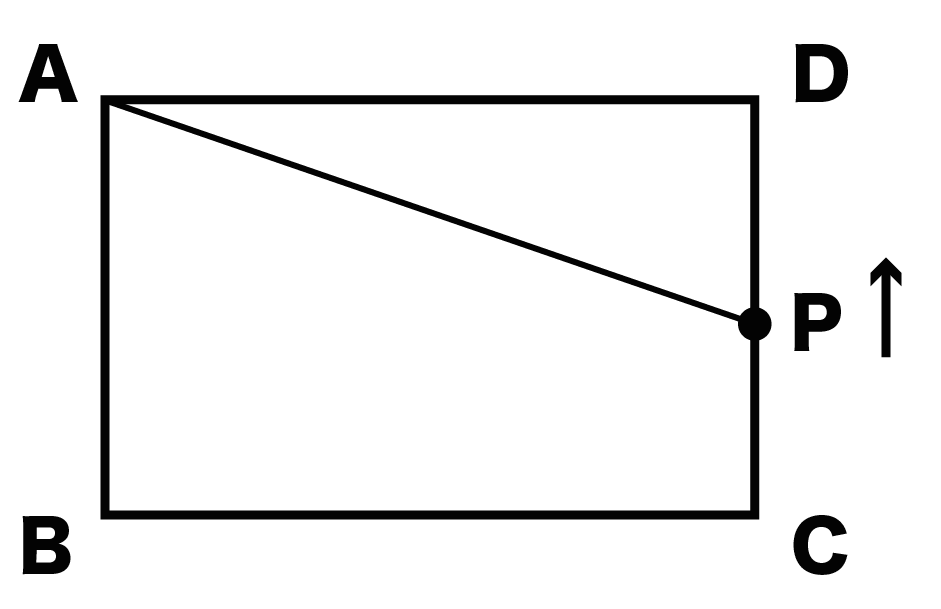
このときの△APDの高さって、
線分DPだよね?
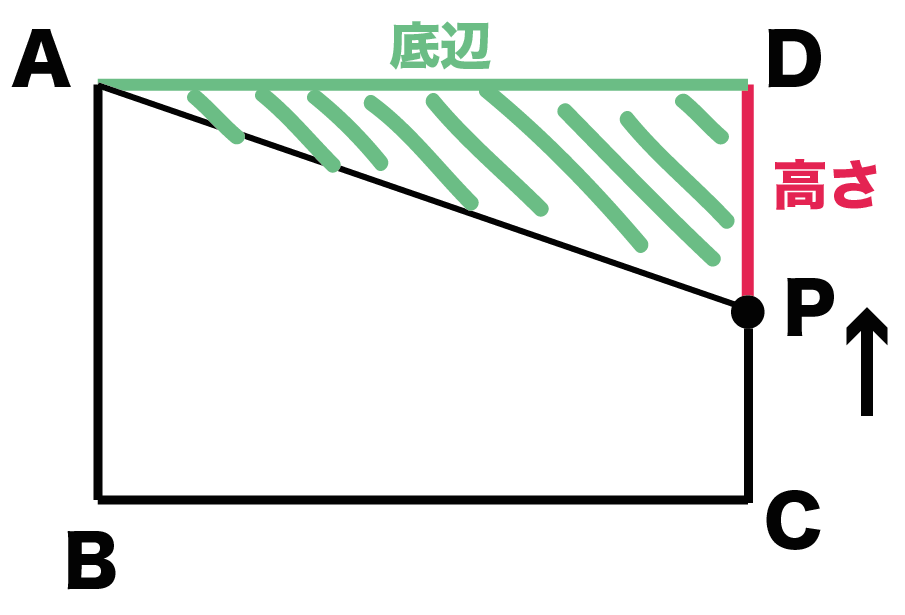
x秒後のDPの長さをだしてやれば、
△APDの面積yを式であらわせるってこさ。
このときの高さDPは、
「3つの辺(AB・BC・CD)」 – 「 Pが動いた距離」
で計算できるよ。
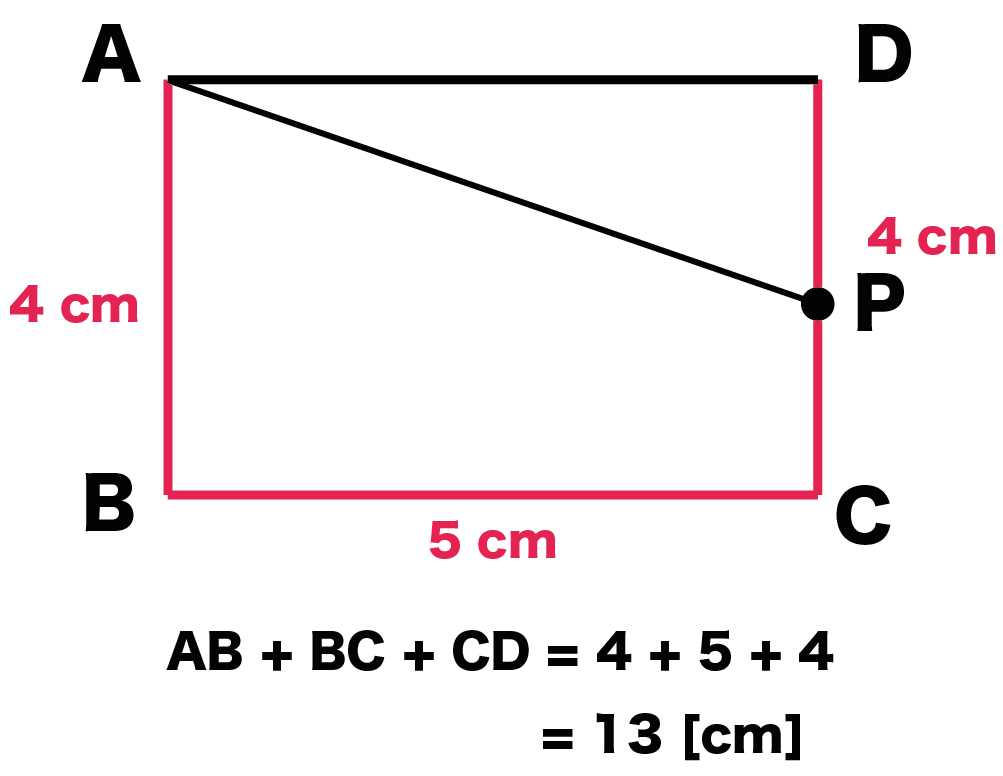
(3つの辺の長さ)= 4 + 5 + 4
= 13 [cm]
になる。
そんで、x秒後に「Pが動いた距離」は、
x [cm]
だね。
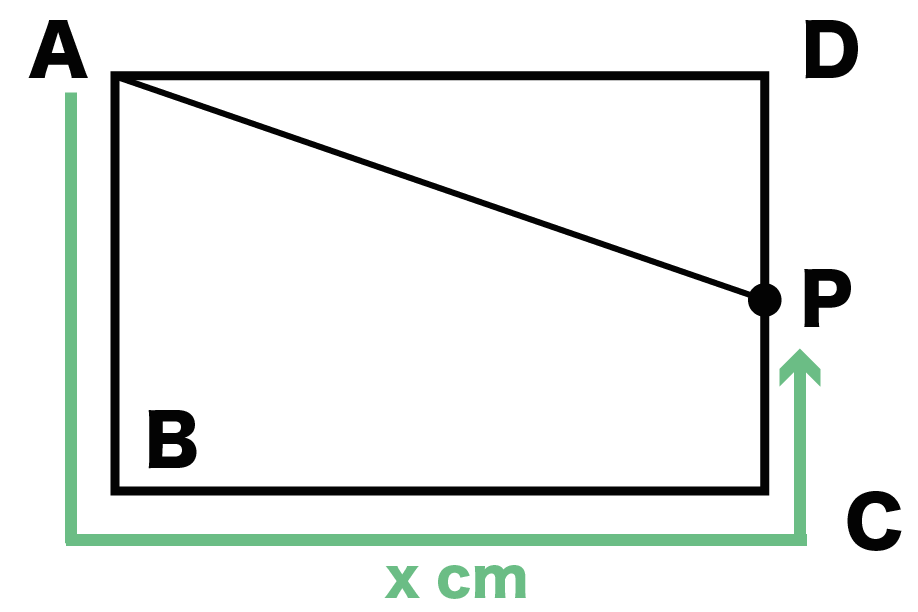
ってことで、
DPの長さは(3つの辺の長さ)- (Pが動いた距離)で求めることができるので、
13 – x
になるね。
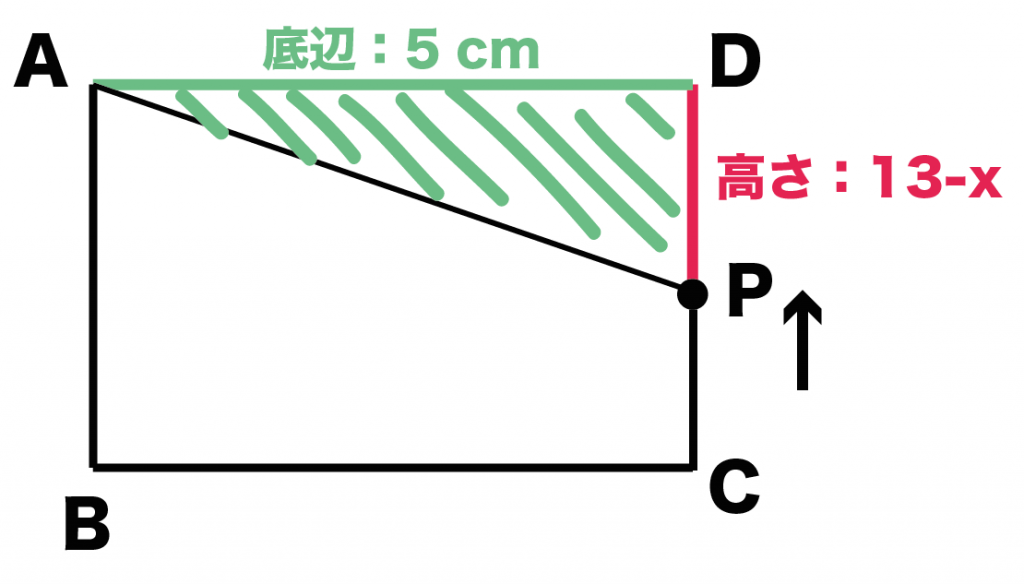
よって、Pが辺CD上を動くとき(9 ≦ x ≦ 13)、
△APDの面積 = 底辺AD × 高さDP × 1/2
= 5 × (13-x) × 1/2
= 5/2 (13-x)
となる。
よって、こいつをグラフに表してやると、
こうなるね↓↓
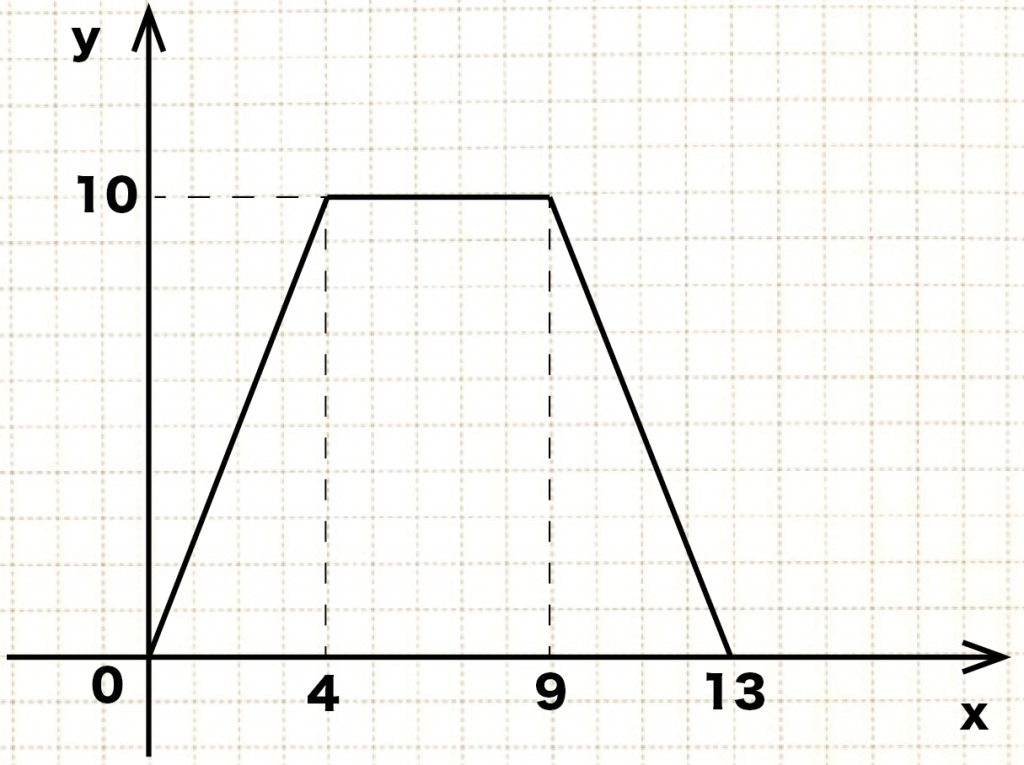
△APDの面積yをxであらわすことができて、
それをグラフにすれば完ぺきだ!
テストに出やすい問題だからしっかりおさえておこう。
まとめ:一次関数の利用の動点は3つのフェーズにわけるべし
動点の問題はどうだった?
フェーズごとに面積の変化が異なる
ってことさえ押さえておけば十分さ。
あとは、
どの辺が底辺・高さになっているのか??
ということに注意してみてね。
そんじゃねー
Ken