【中2数学】一次関数のグラフの書き方がわかる3ステップ
一次関数のグラフの書き方がわからない??
こんにちは!この記事をかいているKenだよ。担々麺うますぎだね。
一次関数という単元は、
グラフの書き方がわかればどうにかなる。
もうね、ほんとね、どうにかなる。
だって、グラフの問題がたくさんでるからね。
グラフをかければ一次関数をマスターしたようなもんさ。

今日はそんな1次関数の攻略のカギをにぎる、
一次関数のグラフの書き方
を3ステップで紹介していくよ。
よかったら参考にしてみてね。
一次関数のグラフの書き方がわかる3ステップ
書き方の基本は、
グラフが通るであろう2点を結ぶ
ということだ。
なぜなら、
一次関数のグラフはゼッタイに直線になるからね。
2点をむすべば直線がかけちゃうんだ。
ってことは、
直線が通る2点をさがせばゲームクリアってわけ。
例題をといてみよう。
つぎの一次関数のグラフをかきなさい。
y = 3/5 x -2
つぎの3ステップでグラフがかけちゃうんだ。
Step1. y軸とグラフの交点をうつ
「y軸」と「一次関数」の交点をうとう。
切片を「y座標」とする点を「y軸上」にとってやればいいんだ。
例題をみてみよう。
一次関数の切片は、
xもyもついていない項のこと
だったね。
例題の関数では、
「xもyもついていない項」って「-2」だよね?
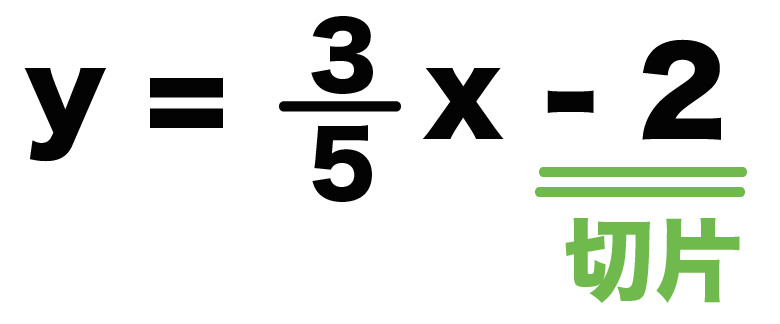
ってことは、コイツが切片だ。
この切片をy座標とするy軸上の点(0, -2)をうっちゃおう。
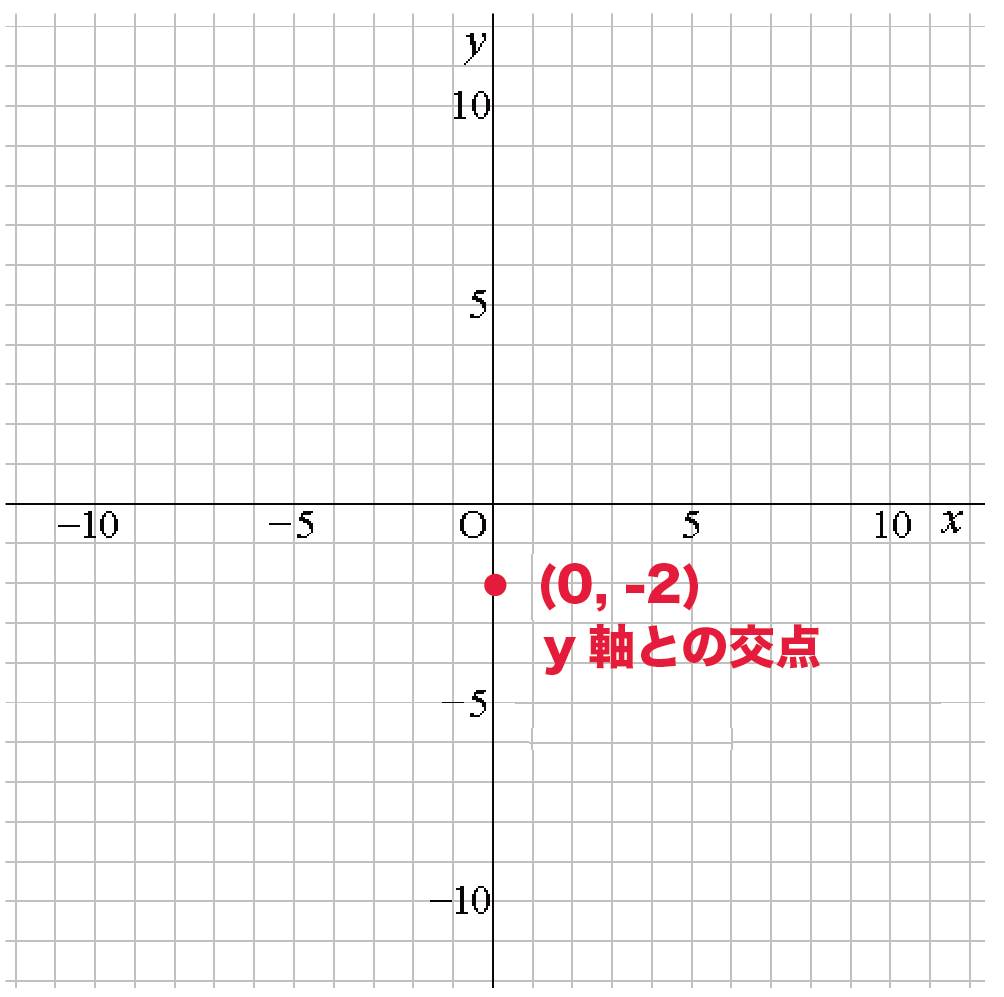
これが1つ目の点だ。
Step2. xもyも整数になる点をうつ!
つぎは「xもyも整数になる点」を打とう。
xに適当な整数を代入して座標をだしてみて。
傾きが整数のときはxに「1」をいれてやればいいね。
ただ、例題みたいに傾きが分数の場合は、
「分母の数字」をxに代入してみよう。
xもyも整数の点がゲットできるはずさ。
例題をみてみよう。
傾きは3/5。
だから、xに分母の「5」を代入してみよう。
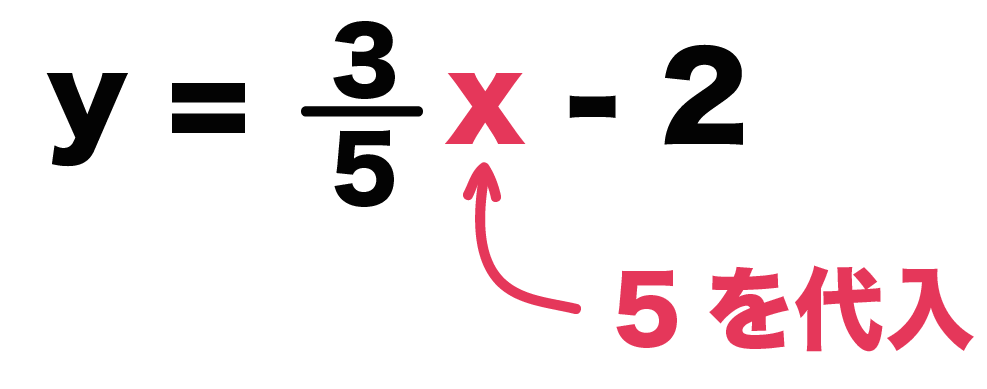
すると、
y = 3/5 × 5 -2
= 1
ってなるでしょ?
つまり、この一次関数は「整数の座標(5, 1)」を通るわけさ。
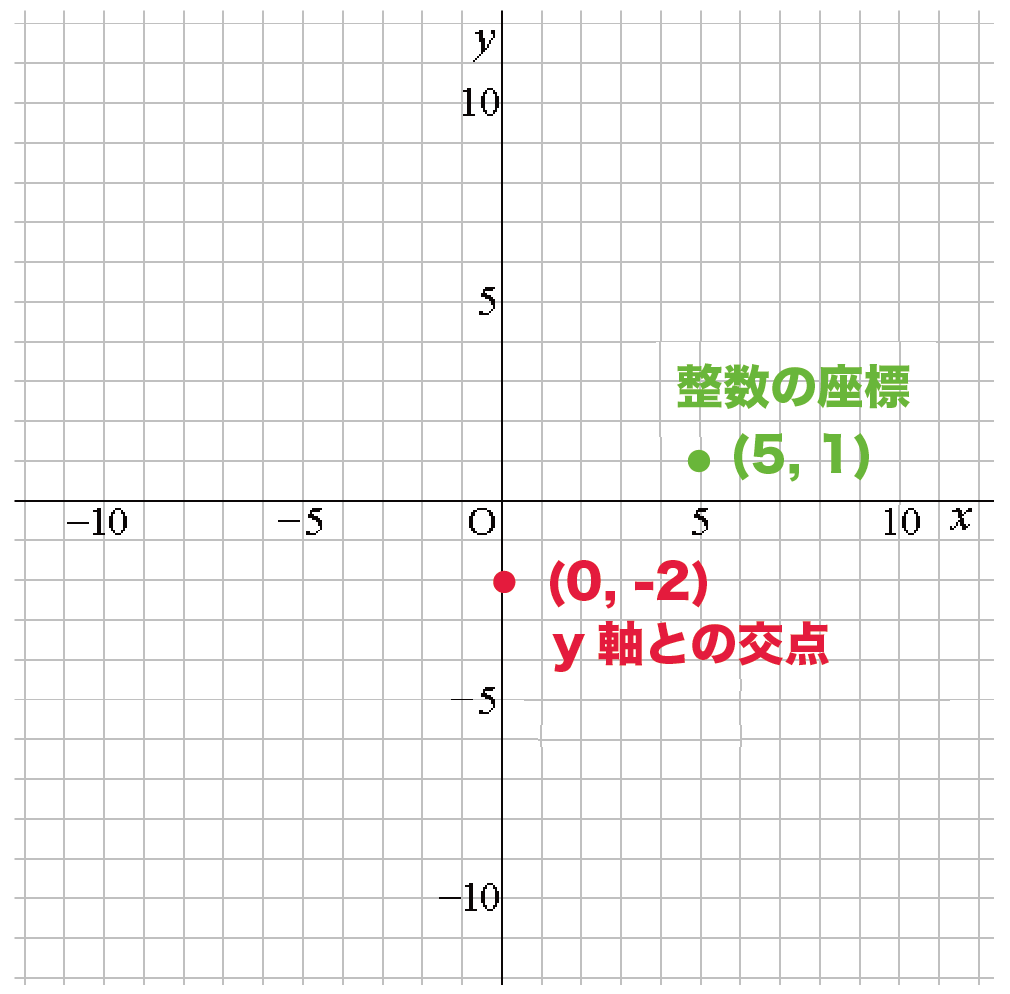
これで2点目がわかったね!
Step3. 直線上の2点をむすぶ!
あとは2点をむすぶだけ。
定規で直線をひいてみよう。
できた直線が一次関数ってわけさ!
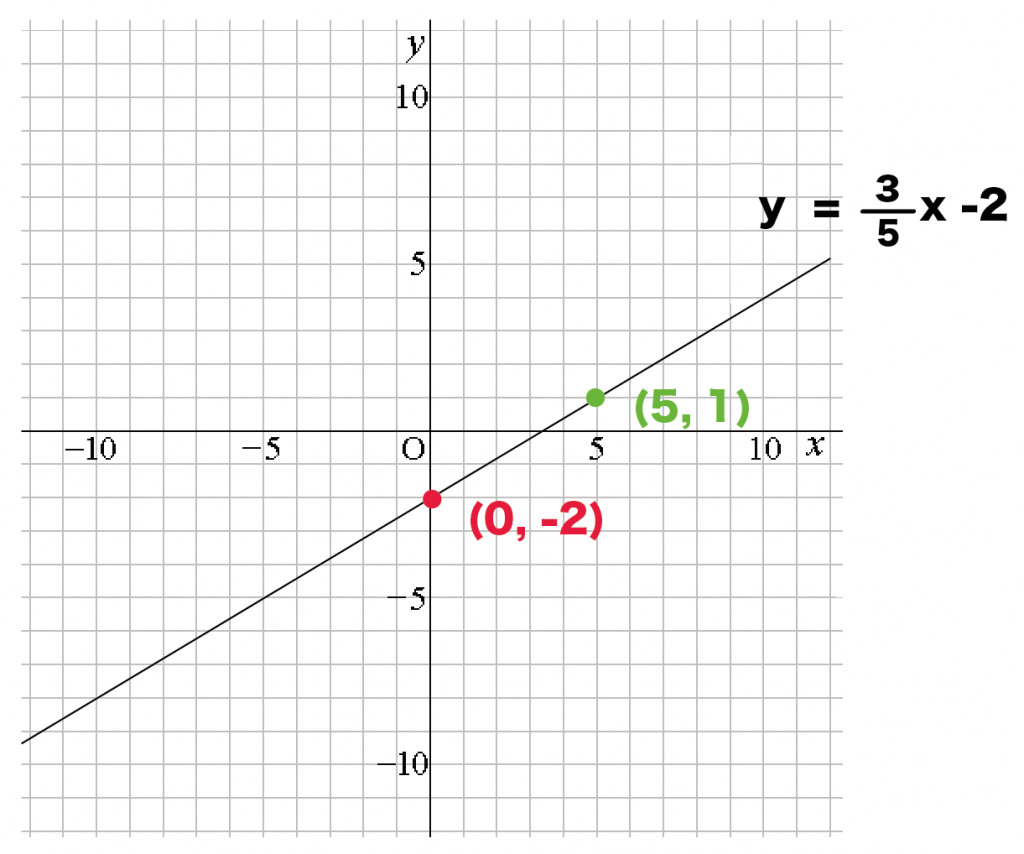
例題では、
- y軸との交点(0, -2)
- 整数の座標(5, 1)
をむすんでみよう。
すると、こんな感じになるっしょ? ↓↓
おめでとう!
1次関数のグラフがかけたね。
まとめ:一次関数のグラフの書き方は「2点をむすぶ」だけ!
一次関数のグラフはむずかしくない。
- y軸との交点
- 整数の座標
をむすんであげればいいんだ。
あとは問題になれてみてね。
そんじゃねー
Ken